數(shù)形結(jié)合 “說”出精彩

蔣世雷 鄭閩

［摘 ?要］ 在分數(shù)乘除法解決問題的教學中，教師應(yīng)借助幾何直觀、數(shù)形結(jié)合等方法，讓學生深刻理解分數(shù)和分數(shù)乘法的意義，加強基本數(shù)量關(guān)系和各類解決問題的算理及算法的口述訓練，溝通與其他相關(guān)知識的聯(lián)系，幫助學生厘清并拓展解決問題的思路。

［關(guān)鍵詞］ 分數(shù)乘除法；解決問題；幾何直觀；數(shù)形結(jié)合；口述訓練

與整數(shù)、小數(shù)的解決問題相比，分數(shù)乘除法解決問題由于數(shù)量關(guān)系比較抽象，學生理解難度增大，因此一直是解決問題教學中的一個難點。怎樣突破這一教學難點呢？筆者認為，教師應(yīng)整體把握分數(shù)乘除法解決問題的教學內(nèi)容，關(guān)注教學內(nèi)容自身的結(jié)構(gòu)化，處理好教學內(nèi)容的整體性、一致性和階段性等關(guān)系，緊扣分數(shù)的意義和分數(shù)乘法的意義，借助實物圖、直條圖、線段圖等幾何直觀手段，讓學生建立形與數(shù)的聯(lián)系，構(gòu)建數(shù)學問題的直觀模型，并利用圖表分析實際情境與數(shù)學問題，探索出各類解決問題的思路。

分數(shù)乘除法解決問題的教學，從縱的方面來說，要提前訓練，多層次孕伏；從橫的方面來說，一要充分揭示分數(shù)乘除法解決問題本身各要素之間的關(guān)系，加強基本數(shù)量關(guān)系的訓練，二要溝通與此有關(guān)的其他知識（如倍數(shù)、比等）的聯(lián)系。在教學中，教師應(yīng)如何利用幾何直觀來加強學生解決問題分析思路的口述訓練呢？

一、借助直觀，深度理解

在分數(shù)乘除法解決問題的教學中，教師應(yīng)整體把握教學內(nèi)容，厘清層次，提前規(guī)劃訓練，步步孕伏鋪墊，運用幾何直觀手段、數(shù)形結(jié)合等方法，從分率句（即用分數(shù)反映兩個量之間的關(guān)系句）入手，引導學生緊扣分數(shù)的意義理解分率句所反映的兩個量的倍比關(guān)系，在理解的基礎(chǔ)上厘清數(shù)量關(guān)系，探尋解題思路，為形成算法漸次過渡。

1.結(jié)合分數(shù)的意義用份數(shù)理解分率句，提前孕伏

到了五年級下期，學生開始系統(tǒng)地認識分數(shù)的意義，對分數(shù)的認識更加抽象。學生真正理解分數(shù)，特別是對分率句的理解，這需要一個長期漸進的過程。

（1）包含關(guān)系分率句的理解。

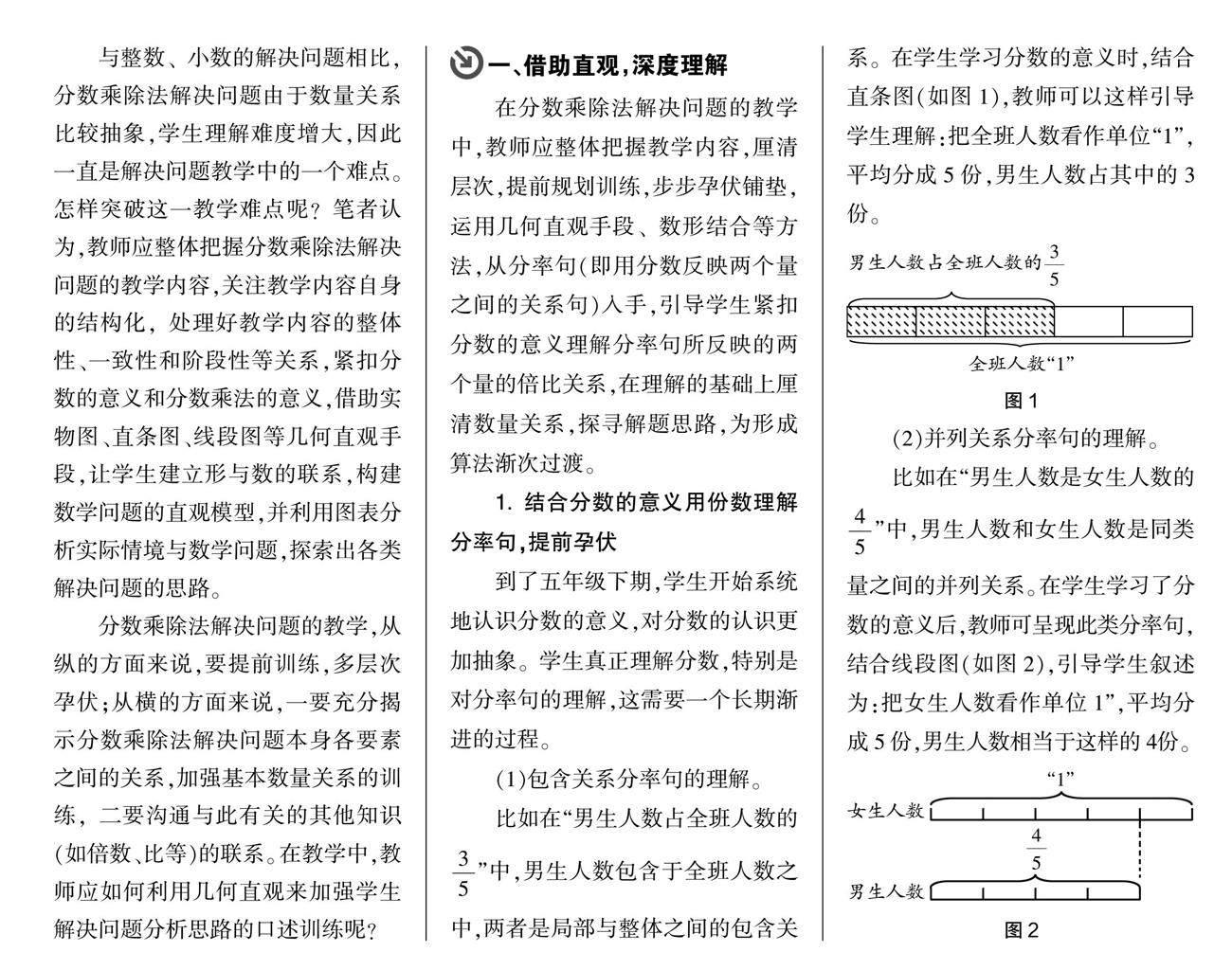
比如在“男生人數(shù)占全班人數(shù)的”中，男生人數(shù)包含于全班人數(shù)之中，兩者是局部與整體之間的包含關(guān)系。在學生學習分數(shù)的意義時，結(jié)合直條圖（如圖1），教師可以這樣引導學生理解：把全班人數(shù)看作單位“1”，平均分成5份，男生人數(shù)占其中的3份。

（2）并列關(guān)系分率句的理解。

比如在“男生人數(shù)是女生人數(shù)的”中，男生人數(shù)和女生人數(shù)是同類量之間的并列關(guān)系。在學生學習了分數(shù)的意義后，教師可呈現(xiàn)此類分率句，結(jié)合線段圖（如圖2），引導學生敘述為：把女生人數(shù)看作單位1”，平均分成5份，男生人數(shù)相當于這樣的4份。

此類口述訓練，既加深了學生對分數(shù)意義的理解，又溝通了分數(shù)與份數(shù)的聯(lián)系，同時為用份數(shù)來解決與分數(shù)乘除法相關(guān)的問題做了提前孕伏，可謂“一石三鳥”。敘述時教師可以用課件逐步呈現(xiàn)直條圖或線段圖，幫助學生更好地用份數(shù)來理解。

2. 分數(shù)乘法計算教學中透徹理解一個數(shù)乘分數(shù)的實際意義

在六年級的分數(shù)乘法的計算教學中，教師要讓學生知道：分數(shù)乘整數(shù)的意義和整數(shù)乘法的意義相同，都是求幾個相同加數(shù)的和，即求幾個幾是多少；一個數(shù)乘分數(shù)的意義，就是求一個數(shù)的幾分之幾是多少。前者體現(xiàn)出整數(shù)、小數(shù)、分數(shù)乘法意義的一致性，學生容易理解，教學時教師應(yīng)重點關(guān)注后者。在分數(shù)乘法的計算教學中，教師應(yīng)如何通過數(shù)形結(jié)合提前孕伏，幫助學生理解透一個數(shù)乘分數(shù)的意義呢？

比如，教師可以出示以下練習：

（1）你能畫圖分別表示出8個蘋果、12個蘋果的嗎？

（2）8個蘋果的是幾個蘋果？12個蘋果的是幾個蘋果？說一說你是怎么想的？

（3）都是這些蘋果的，為什么蘋果的個數(shù)不一樣？

在第（2）個問題中，教師可以引導學生這樣敘述理解：8個蘋果的是把8個蘋果看作單位“1”，平均分成4份，每份是8÷4=2（個），其中的3份就是2×3=6（個）蘋果，所以8個蘋果的是6個蘋果。同樣，12個蘋果的是把12個蘋果看作單位“1”，平均分成4份，每份是12÷4=3（個），其中的3份就是3×3=9（個）蘋果，所以12個蘋果的是9個蘋果。通過這樣的口述訓練，學生弄清了求一個數(shù)的，根據(jù)分數(shù)的意義，就是把這個數(shù)平均分成4份，取其中的3份是多少，由此幫助學生建立起分數(shù)的意義與求一個數(shù)的幾分之幾的內(nèi)在聯(lián)系（如圖3）。

在上面的練習中，教師通過數(shù)形結(jié)合恰當?shù)靥幚砹酥庇^與抽象的關(guān)系，引導學生通過對數(shù)學內(nèi)容的直觀表述既理解了的意義，還理解了由于單位“1”不同，同樣是單位“1”的，但是所表示具體數(shù)量并不相同。這樣的練習溝通了一個數(shù)乘分數(shù)的實際意義與分數(shù)的意義之間的聯(lián)系，為以后的分數(shù)乘法中用“求一個數(shù)的幾分之幾是多少”來解決問題做好了鋪墊。

3. 強化“求一個數(shù)的幾分之幾是多少”解決問題中解題思路的口述訓練

學生透徹理解了一個數(shù)乘分數(shù)的意義后，教師即可在分數(shù)乘法的解決問題教學中強化“求一個數(shù)的幾分之幾是多少”解題思路的口述訓練。眾所周知，在分數(shù)乘除法的解決問題教學中，簡單的用分數(shù)乘法解決問題是基礎(chǔ)。因此，在分數(shù)乘法的計算教學中，教師要充分結(jié)合分數(shù)乘法的意義，在具體的問題情景中借助線段圖或直觀圖讓學生充分感知并理解一個數(shù)乘分數(shù)的意義，就是求這個數(shù)的幾分之幾是多少。

（1）簡單的“求一個數(shù)的幾分之幾是多少”？

西南大學版教材六年級上冊分數(shù)乘法例題：從甲地到乙地共有84千米，已經(jīng)行了全程的，汽車已經(jīng)行了多少千米？

教師先引導學生畫出線段圖（如圖4），然后引導學生結(jié)合線段圖從分率句入手，用份數(shù)和一個數(shù)乘分數(shù)的意義分析解題的思路。

①用份數(shù)分析：“行了全程的”，把全程看作單位“1”，平均分成3份，行了的路程占其中的2份。已知全程是84千米，平均分成3份，每份是84÷3=28（千米），2份是28×2=56（千米）。列式為：84÷3×2=56（千米）。

②用一個數(shù)乘分數(shù)的意義分析：“行了全程的”是指已經(jīng)行了的路程占全程的，把全程看作單位“1”，已經(jīng)行了的路程=全程×，已知全程是84千米，求已經(jīng)行了多少千米，就是求84千米的是多少，用乘法算，列式為：84×=56（千米）。

（2）稍復雜的“求一個數(shù)的幾分之幾是多少”？

如前所述，在用分數(shù)乘除法解決問題中，簡單的用分數(shù)乘法解決問題是基礎(chǔ)和關(guān)鍵。如果學生掌握了用分數(shù)乘法解決問題的解題思路，在面對稍復雜的用分數(shù)乘除法解決問題時，也能從基本的數(shù)量關(guān)系和基本的解法遷移拓展過去。

比如在教學“足球有20個，籃球的個數(shù)比足球多，籃球有多少個”時，教師先引導學生理解題意，畫出線段圖（如圖5），然后結(jié)合線段圖，從分率句入手用不同的思路進行分析。

分析一：“籃球的個數(shù)比足球多”，是把足球的個數(shù)看作單位“1”，籃球的個數(shù)相當于足球個數(shù)的1+，已知足球有20個，求籃球有多少個，就是求20個的1+是多少，列式為：20×1+=25（個）。

分析二：“籃球的個數(shù)比足球多”，是把足球的個數(shù)看作單位“1”，籃球比足球多的個數(shù)相當于足球個數(shù)的。已知足球有20個，所以籃球比足球多20×=5（個），再用20+5=25（個）即可求出籃球的個數(shù)。

二、數(shù)形結(jié)合，注重歸類

“結(jié)構(gòu)化”是數(shù)學的學科特點，數(shù)學教學的內(nèi)容、方法都具有高度的結(jié)構(gòu)化特征。因此，在教學過程中，教師要站在整體、系統(tǒng)和結(jié)構(gòu)的高度把握、處理教學內(nèi)容，從數(shù)學知識結(jié)構(gòu)和學生認知結(jié)構(gòu)出發(fā)設(shè)計與組織教學。在分數(shù)乘除法解決問題的教學中，教師要幫助學生借助實物圖或線段圖等直觀圖示，厘清各種基本類型的結(jié)構(gòu)，在各種類型的解決問題教學中加強口述訓練，幫助學生弄清分析問題的思路，從而提升學生分析問題、解決問題的能力。

比如，在“求一個數(shù)是另一個數(shù)的幾分之幾是多少”類型的題目解題思路口述訓練時，以解決問題“合唱隊有男生15人，女生20人，男生人數(shù)是女生人數(shù)的幾分之幾”為例，教師應(yīng)緊扣分數(shù)的意義，引導學生這樣分析：求“男生人數(shù)是女生人數(shù)的幾分之幾”，是把“男生人數(shù)”同“女生人數(shù)”做比較，因此“女生人數(shù)”是標準，是單位“1”。題目中“男生有15人，女生有20人”，根據(jù)分數(shù)的意義，可以這樣想：把“女生人數(shù)”看作單位“1”，平均分成20份，男生有這樣的15份，所以男生人數(shù)是女生人數(shù)的，列式為：15÷20=。

大部分教材都將“求一個數(shù)是另一個數(shù)的幾分之幾”的教學安排在“分數(shù)的意義”教學之后，此時學生還沒有學習約分等知識。如果學生學習了約分以后，教師可以引導學生將5個人作為1份，畫出實物圖（如圖6）或線段圖（如圖7），然后采用數(shù)形結(jié)合的方法引導學生分析：如果把5個人作為1份，求男生人數(shù)是女生人數(shù)的幾分之幾，是把女生人數(shù)看作單位“1”，平均分成20÷5=4份，男生有這樣的15÷5=3份，所以男生人數(shù)是女生人數(shù)的。列式為：15÷20==。

三、運用圖表，溝通關(guān)聯(lián)

1. 厘清乘除法的關(guān)聯(lián)性，根據(jù)乘除法的互逆關(guān)系完善基本數(shù)量關(guān)系和解決思路的口述訓練

在學生理解了“一個數(shù)乘分數(shù)，就是求這個數(shù)的幾分之幾”這一含義后，筆者要求學生先讀分率句，找出單位“1”，然后說出基本的數(shù)量關(guān)系。比如在“男生人數(shù)是女生人數(shù)的”中，筆者引導學生這樣理解：“把女生人數(shù)看作單位‘1，男生人數(shù)＝女生人數(shù)×。”在充分理解算理的基礎(chǔ)上，學生根據(jù)乘除法的互逆關(guān)系得出“女生人數(shù)＝男生人數(shù)÷”后，還可以開展這一數(shù)量關(guān)系的口述訓練（如表1）。這樣學生對基本的用分數(shù)乘除法解決問題的算理理解更深刻，算法形成更清晰，更易于知識的系統(tǒng)化。

如前所述，在用分數(shù)乘除法解決問題中，簡單的用分數(shù)乘法解決問題是基礎(chǔ)和關(guān)鍵。如果學生掌握了用分數(shù)乘法解決問題的解題思路，在教學“已知一個數(shù)的幾分之幾是多少，求這個數(shù)”時，學生自然而然就會想到用方程解或根據(jù)乘除法的互逆關(guān)系來解答。在解答稍復雜的用分數(shù)乘除法解答的解決問題時，學生也能從基本的數(shù)量關(guān)系和基本的解法遷移拓展過去。

2. 聯(lián)想訓練

實踐證明，在教學用分數(shù)乘除法來解決問題的教學中，“多想幾步”這種訓練方法，對打開學生思路和提高解題能力很有幫助。比如“一段路，已修了全長的”，要求學生想到“還剩全長的”；“一堆煤，第一次運走這堆煤的，第二次運走這堆煤的”，要求學生想到“兩次共運走這堆煤的”“第二次比第一次多運走這堆煤的”“還剩下這堆煤的1－－＝”（見表2）。

“多想”是根據(jù)整體與部分之間的內(nèi)在聯(lián)系、部分與部分之間的內(nèi)在聯(lián)系來實現(xiàn)的。經(jīng)過“多想幾步”訓練，可以使題目中隱含的數(shù)量明朗化，開闊學生的解題思路，提高學生的解題能力。

3. 溝通與其他知識的聯(lián)系

在分數(shù)乘除法解決問題的教學中，教師要適度引導學生結(jié)合所學的其他知識進行溝通訓練，實現(xiàn)知識上的融會貫通。比如在比的相關(guān)知識教學后，教師應(yīng)重點引導學生找出整體與部分之間、部分與部分之間存在的各種倍比關(guān)系，并將相關(guān)的兩個量之間的比和分率關(guān)系之間的相互轉(zhuǎn)化清晰地表述出來，把分數(shù)、份數(shù)、倍數(shù)、比等相關(guān)知識聯(lián)系起來。比如，對于“蘋果樹的棵數(shù)比梨樹多”，教師可以引領(lǐng)學生從不同角度理解和口述（如表3）。

在此基礎(chǔ)上，教師還可以通過設(shè)計題組來溝通用分數(shù)乘除法解決問題和用份數(shù)、倍數(shù)、比的知識等來解決問題之間的聯(lián)系，以形成更宏大的知識體系。這為學生掌握、拓展并優(yōu)化解決問題的策略提供了堅實的基礎(chǔ)，進一步培養(yǎng)學生的學習能力、實踐能力和創(chuàng)新能力。

總之，幾何直觀有助于學生把握問題的本質(zhì)和明晰思維的路徑。在分數(shù)乘除法解決問題的教學中，教師應(yīng)從整體把握好教學內(nèi)容，利用實物圖、條形圖、線段圖等幾何直觀、數(shù)形結(jié)合等方法，提前孕伏，層層深入，讓學生深刻理解分數(shù)和分數(shù)乘除法的意義，注重各種類型解決問題思路的口述訓練，利用圖表溝通與其他相關(guān)知識的聯(lián)系，探索出解決問題的多種思路，從而達到理想的教學效果。