巧用函數思想妙解平面幾何問題

黃永慧

摘要：函數思想是用函數的概念和性質去分析問題、解決問題的思維策略，它是初中數學的重要思想之一.在解答幾何問題時，常常會遇到根據已知條件很難直接通過演繹推理求解或證明的情況，但如果能建立適當的平面直角坐標系，利用數形結合思想，結合函數解析式來解決，往往能出奇制勝，事半功倍.本文中就利用一次函數、三角函數及二次函數來妙解平面幾何問題展開論述.

關鍵詞：函數思想；妙解；平面幾何問題；函數解析式；最值；動態問題

函數思想（Theory and thought of function）是解決“數學型”問題中的一種思維策略.自人們運用函數以來，經過長期的研究和摸索，科學界普遍有了一種意識，那就是函數思想，在運用這種思維策略去解決問題時，科學家們發現它們都有著共同的屬性，那就是定量和變量之間的聯系.

回顧數學發展的歷史，早在幾百年之前法國著名的數學家笛卡兒就曾提出過所謂的“萬能方法”，這種方法就是把函數思想應用到幾何中去，把幾何問題轉化為代數問題，再把代數問題歸結為函數問題來解決.

解決此類問題的過程中，要善于挖掘題目中的隱含條件，構造出函數解析式和妙用函數的性質，是應用函數思想的關鍵.對所給問題的觀察、分析與判斷比較深入和充分時，會產生由此及彼的聯系，構造出函數原型.另外，方程問題、不等式問題和某些代數問題也可以轉化為與其有關的函數問題，即用函數思想解答非函數問題.

1 巧建平面直角坐標系利用函數妙解線段問題

在教學過程中發現，凡是可以運用函數解析法來解決的一些問題，它們的條件大都有鮮明的特征，即具備建立平面直角坐標系的條件.如在通常情況下，可以根據相對應的條件，選取合適的點為坐標原點，互相垂直的線段所在的直線為坐標軸建立平面直角坐標系來解答問題，會起到事半功倍的效果^［1］.

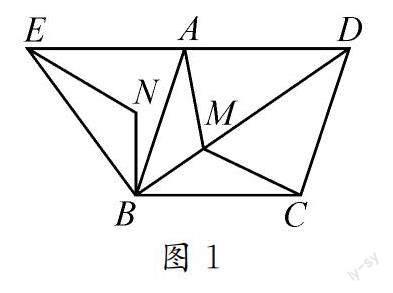
例1 如圖1，四邊形ABCD是菱形，且∠ABC＝60°，△ABE是等邊三角形，M為對角線BD（不含B點）上任意一點，將BM繞點B逆時針旋轉60°得到BN，連接EN，AM，CM.

（1）求證：△EBN≌△ABM.

（2）當點M在何處時，AM+BM+CM的值最小？請說明理由.

（3）在（2）的條件下，若菱形ABCD的邊長為2，求BM的長度.

分析：（1）顯然，根據△ABE是等邊三角形和菱形ABCD的性質可證明△EBN≌△ABM.

（2）連接CE，當點M位于BD與CE的交點處時，AM+BM+CM的值最小，求出EC的值即可.

（3）根據題意可以發現BN⊥BC，M又是BD和EC的交點，故可以考慮根據一次函數圖象的交點來解決點M的坐標問題，從而很容易的得到BM的長度.

根據題意建立以B為原點，以BC所在直線為x軸，以BN所在直線為y軸的平面直角坐標系，再結合菱形的性質可求出直線BD和直線CE的解析式，求出交點坐標，進而求解.

2 巧用一次函數解答動態三角形面積問題

動態面積類問題一直是學生害怕的難點問題，由于動點變化引起其他圖形變化，因此在圖形變化過程中很難確定具體的數量關系.這種情況下可以考慮采用函數關系來分析，即用含自變量的代數式表示因變量，根據獲得的解析式進行求解會讓問題變得簡單容易^［2］.

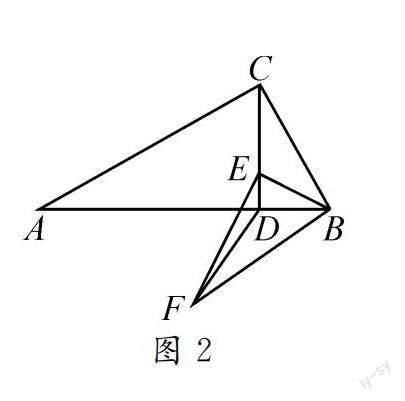
例2 如圖2，在△ABC中，AB＝1，CD⊥AB于點D，E是線段CD上的動點，點F在直線AB的下方，∠ACB＝∠FEB＝90°，∠A＝∠EFB＝30°，試探求CE的長與△BDF的面積關系.

分析：由于點E是線段CD上的一個動點，因此CE的長度是一個變量，我們可以考慮它是否和△BDF的面積存在一定的函數關系.

3 巧用三角函數解答直角三角形問題

三角函數知識不僅僅可以直接用來解直角三角形，在幾何問題中也可以進行綜合應用，有些問題利用三角函數來解答能使問題更加明朗.如，利用三角函數的定義把握三角形邊與角之間的關系，利用等角的關系可以將不同三角形的邊之間的關系聯系在一起，進一步優化解題思路，讓平面幾何問題的解答過程變得更加簡捷、巧妙.

例3 如圖4，Rt△ABC中有正方形DEFG，點D，G分別在AB，AC上，點E，F在斜邊BC上，求證：EF²=BE·FC.

證明：因為∠A=90°，且∠CGF+∠C=∠B+∠C，所以∠CGF=∠B.在Rt△BDE中，tan B=DEBE;在Rt△CFG中，tan? ∠CGF=CFFG.又根據已知條件可得DE=FG=EF，故EF²=BE·FC.

4 巧用二次函數解答四邊形最值問題

二次函數最重要的作用之一就是利用函數解析式求解最值問題，因此在最值求解過程中，可以利用所給條件，列出二次函數的解析式，借助解析式分析最大值或最小值，也可以借助二次函數圖象判斷最值問題.

例5 某市進行河灘治理，優化美化人居生態環境.如圖5所示，在河畔的一處灘地上規劃一個五邊形河畔公園ABCDE.按設計要求，要在五邊形河畔公園ABCDE內挖一個四邊形人工湖OPMN，使點O，P，M，N分別在邊BC，CD，AE，AB上，且滿足BO＝2AN＝2CP，AM＝OC.已知五邊形ABCDE中，∠A＝∠B＝∠C＝90°，AB＝800 m，BC＝1 200 m，CD＝600 m，AE＝900 m.為滿足人工湖周邊各功能場所及綠化用地需要，想讓人工湖面積盡可能小.請問，是否存在符合設計要求的面積最小的四邊形人工湖OPMN？若存在，求四邊形OPMN面積的最小值及這時點N到點A的距離；若不存在，請說明理由.

解析：根據圖形特點，將圖形補齊，如圖6，分別延長AE與CD，交于點K，則四邊形ABCK是矩形.設AN＝x，則PC＝x，BO＝2x，BN＝800-x，AM＝OC＝1 200-2x，MK＝2x，PK＝800-x，進而得出S四邊形OPMN＝4（x-350）²+470 000，故當點N到點A的距離為350 m時，四邊形OPMN面積的最小值為470 000 m².

當然，運用二次函數可以解決很多貼近生活實際的幾何圖形問題，取得最值的情況需要具體分析.一是在二次函數圖象的頂點處取最值；二是要對多個函數分別求得最值后再通過比較獲取最值；三是在不包括二次函數對稱軸的一側取得最值；四是在對稱軸附近的整點處獲取最值.特別是在解決具體實際應用題時，要注意根據題意靈活把握函數的有關性質，并與函數圖象結合起來進行求解.

函數思想在應用過程中具有廣泛性、多樣性和靈活性，在教學中要重視函數思想的滲透，引導學生充分挖掘平面幾何問題中的函數思想，能夠巧用函數定義、性質、圖象來分析問題，轉化問題，解答問題，從而不斷提升思維品質和數學綜合素養.

參考文獻：

［1］薛朝暉.平面直角坐標系中數形結合思想之巧用［J］.初中生世界，2015（6）：22-23.

［2］武芳.談談函數思想在解題中的應用［J］.語數外學習（高中版下旬），2022（3）：56.