章頭課教學探索

王星

摘 要： 一元一次方程是初中階段“數與代數”部分的重要內容，也是數學中的基本運算工具，對學生培養分析問題、解決問題的能力、體會數學的價值具有重要意義.同時，一元一次方程也是以后學習二元一次方程組、一元一次不等式（組）及一元二次方程的基礎，是刻畫現實世界中數量關系重要模型.章頭課是對一章內容的概括，通過學習，學生可以初步了解到本章將要學習的內容、研究的方向，構建知識結構框架，更加系統和有條理地完成新的一章的學習.

關鍵詞： 一元一次方程；章頭課；思考

我有幸受邀執教了一節蘇科版七年級上冊第4章“一元一次方程”的章頭課，這次活動讓我對章頭課有了初步的認識與思考，現將幾點認識及思考總結如下，與同行分享.

1 教學內容解讀

蘇科版教材每章的開頭部分都設計安排了“章頭語和章頭圖”.章頭課作為一章內容的起始課，涵蓋了整章的學習內容、思想方法，就“一元一次方程”而言，教材安排了飛馳的賽車和平衡的天平作為章節開頭的素材，章頭語為：方程，表達數量之間相等關系的“天平”，是解決實際問題的有效模型.章頭語簡潔明了，章頭圖豐富多彩，兩者是本章的重要組成部分，它們體現了數學在生活中的應用價值.教材用一動一靜兩幅圖來表達這種數量的相等關系，說明方程是分析解決問題的有效工具.右邊的天平平衡圖用2x+125表達了質量和砝碼之間的數量關系.讓學生感受到數學語言在生活中的應用.

一元一次方程是學生進入初中后接觸模型思想的第一課，學生需要了解方程、一元一次方程有關概念，理解等式的性質，基本了解本章學習內容和知識框架，經歷一元一次方程解概念形成與初步探究解一元一次方程的過程，體會模型的思想和從特殊到一般的數學思想.筆者反復斟酌教材的編寫意圖，設計了如下的教學過程：

2 課堂教學及說明

2.1 設計情境，貼近生活

活動一： ?年齡的問題

剛剛我與這位同學交流了一下，發現我的年齡是他的三倍還多8歲，你能用所學的代數式來表示年齡關系嗎？若知道我今年44歲，你能求出這位同學的年齡嗎？這樣的等式你能自己編一個嗎？如：幾年后我倆年齡之和是100歲？幾年后我的年齡恰好是這位同學年齡的3倍？

設計意圖： ?好的課堂一定是學生自主的課堂，通過交流年齡問題不僅可以活躍氣氛還可以直接引入主題，而且還可以提升學生的注意力，激發學生的求知欲，促進學生的積極思維，同時很自然地引出了方程的相關內容，讓學生感受從代數式到方程的形成過程.

2.2 嘗試練習，形成概念

活動二： ?糖果的問題

1. 老師給積極回答問題的同學準備了棒棒糖，每人分4個則少6個，如果每人分3個則多4個，你能知道老師準備給多少名學生發棒棒糖？帶了多少個棒棒糖嗎？

2. ?已知桌子上有兩盒棒棒糖，共50支，我從第一盒里拿 10 個放進第二盒，兩盒棒棒糖就一樣多了.你能知道原來每個盒子中各有多少個棒棒糖嗎？

活動三：

你能自己列舉出生活中具有等量關系且用這種等量關系解決問題的實例嗎？

設計意圖： ?通過學生切入實際的思考后形成4x-6與3x+4的代數式，體會用不同的方法“算兩次”，然后用“=”連接，然后通過類比的方法得到4x-6=3x+4，x-10=50-x+10等式，學生在問題串的引領下有序思考，為學生探究方程指明方向，讓學生感受由未知到已知，從陌生到熟悉的探索過程.

2.3 嘗試練習，形成概念

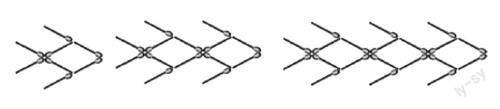
利用課本習題圖進行追問：

搭1條，2條，3條“小魚”各用多少根火柴棒？按同樣方式，搭20條“小魚”要用多少根火柴棒？

反之，我若給你140根火柴棒你能搭多少條小魚呢？

設計意圖： ?通過學生熟悉的“小魚”問題結合剛剛的含有未知數的等式，形成如下定義：只含有一個未知數且未知數的次數都是1次的整式方程叫一元一次方程.此處是課堂的高潮之一，因為學生在上課過程中竟然搶著寫，并且有學生主動提出嘗試寫一元二次方程與二元一次方程等，筆者在點評學生回答的同時形成板書，增加印象，并為后面的學習做好鋪墊工作.

2.4 依據經驗，嘗試解法

丟番圖被認為是代數學的鼻祖，但歷史上沒有一本正式的著作里留下他完整的生平，甚至連他的國籍都沒有明確的記載.然而有趣的是，他竟然有一個墓志銘，上面鐫刻著他的一些情況：“他生命的六分之一是幸福的童年.再活十二分之一，頰上長出了細細須.又過了生命的七分之一才結婚. 再過五年他感到很幸福，得了一個兒子.可是這孩子光輝燦爛的生命只有他父親的一半.兒子死后，老人在悲痛中活了四年，結束了塵世的生涯.” 你知道丟番圖結婚時和去世時的年齡分別是多少嗎？

設計意圖： ?通過對4x-6=3x+4的分析，初步認識了方程的解及解方程并能利用等式的基本性質初步解簡單的一元一次方程.此處讓學生經歷感受、猜想、驗證、探究、應用的過程，讓學生感受解的本質，引發興趣為學生后續深入學習做鋪墊.

當堂反饋

1. 下列方程中，是一元一次方程的是（ ?）.

A. ?x2-4x＝3

B. ?xy-3＝5

C. ?3x-1＝ x 2

D. ?x+2y＝1

2. 在日歷縱列上圈出了三個數，算出它們的和，其中正確的一個是（ ?）.

A. ?28

B. ?34

C. ?45

D. ?75

3. 由“比a的3倍大5的數等于a的4倍”可列一元一次方程： ?????.

4. 解下列各方程：

（1） 3（x-1）＝6；

（2） 2x＝9-x.

設計意圖： ?進行適時反饋訓練是提升教學效果的有效手段，此處用4個不同類型的題目讓學生從定義、形象應用，抽象感知、方程求解展開練習.讓學生感受到使用方程模型的方便簡捷.

2.5 課堂小結

本節課發現了現實問題中隱含的方程，并對發現的方程進行了研究，參照本節課的研究思路和方法，對之后的學習內容你準備如何研究？

設計意圖： ?在學生總結感悟的基礎上進行這樣的提問能有效地形成知識框架，并讓學生形象地感知下面的學習內容，體現了這節章頭課的可延展性和可生長性，培養了學生的探究意識與探究能力，讓學生體會學無止境.

3 教學感悟

章頭課是對一章內容的概括，通過這節課的實踐教學，筆者在實施教學時有以下幾點感悟：

1. 章頭課的實踐教學能有效提高教師對教材的理解能力與再處理能力，筆者研究教材的設計發現從字母到數，從數到式，從式到方程，從方程到不等式、函數都是一條線串起來，我們課堂設計如何用一條線串起來？這是我們備課的重點.

2. 章頭課的教學是單元教學的基礎與實踐，而單元教學能有效提升教學成績要上好單元教學課，教師應從章頭課的研究做起，建立起知識體系，為后續的學習創設好框架與方向.

3. 章頭課的教學不追求教學內容的多少，而在于讓學生形成框架結構、數學模型以及感受數學模型應用的必要性與便捷性.教學以提高數學能力，形成問題意識，發展深度思維為主要方向.本節課的一元一次方程教學就以活動的形式逐步展開，以問題貫穿整個課堂，讓學生感受數學模型應用的必要性與便捷性.

4. 章頭課的教學適宜開門見山，然后進行轉化，從一個生活情境引入，讓數學知識源自生活，高于生活，讓學生感受一元一次方程概念的形成過程，并能聯想類比到一元二次方程、二元一次方程等相關概念.最后的應用實質都是轉化，正如笛卡爾所說“一切問題都可以轉化為數學問題，一切數學問題都可以轉化為代數問題，而一切代數問題又都可以轉化為方程問題.因此，一旦解決了方程問題，一切問題將迎刃而解！”

5. 章頭課的教學中，教師要留給學生足夠的探究空間，要找出能引起學生好奇心，激發其興趣的內容，引導學生積極開展探究活動，在活動中感悟思想方法.在探索方程的解的環節，先回顧等式的基本性質，目的是促使學生利用類比的方法探究方程解的本質，從而將學習方法正遷移.讓學生初步感悟到了方程模型，同時也感知了由特殊到一般再回到特殊的研究方法.這些方法能給學生的思維注入新的活力，為今后的學習鋪路搭橋.

參考文獻：

［1］ 孫凱.整體建構：章頭課的應然追求［J］.上海中學數學，2021（6）：5 7.