“說數學”在教學中的應用研究
牟慶生

摘要:數學是思維的體操,將數學思維過程用語言表達出來,有助于教師了解學生的動態,及時調整教學方向,實現教學相長.本文中以“函數的零點”教學為例,具體闡述如何選擇“說”的內容,并提出“說”的執行方法.說開放話題,制造認知沖突;議議新問題,擬定解決方案;辨析新材料,驗證解題方案;練典型例題,培養表述能力;評教學反饋,增強解題信心.
關鍵詞:說數學;認知;材料
說數學是指學習者用口頭表達的方式闡述自己對數學問題的認識、解題思路、思想方法與情感體會等的過程,一般可概括為:說知識、說過程、說異見、說體會.說數學是數學交流的基本形式,能讓學生在表達中獲得良好的交流能力,為數學核心素養的形成奠定基礎.鑒于此,筆者以“函數的零點”教學為例,具體談談如何將“說數學”應用于實際教學中.
1 選擇說的內容
學生認知發展的過程并不一定與教學過程相符合,其認知常常隨著最近發展區的發展而發展.因此,在說數學的內容選擇上,應契合學生的認知經驗,只有著眼于學生認知的生長點,才能讓說數學起到真正的教學作用.教師應精心設計教學過程,為學生搭建“說”的平臺,并積極配合學生的“說”,讓師生、生生之間通過對話的方式,完成教學任務,實現教學相長.
“函數的零點”教學是在函數概念的基礎上進行的,可利用函數的性質、圖象等解決方程問題,將函數的零點和方程的根融合在一起進行思考、分析.但在數形結合的對應上,學生常會出現偏差,有時因過分倚重一方面,導致其他因素被弱化,所捕捉到的信息不全,出現圖形不準確或數據偏差等問題;也有學生因等價轉化不合理,導致思維出現混亂等情況.
事實證明,解題不僅需要嚴謹的邏輯思維能力,還要有良好的直覺思維,而用語言表達則是訓練學生直覺思維的良好方法.
綜上分析,筆者認為本節課的教學,訓練學生的“說數學”能力可選取以下內容:①回顧零點的概念與判定方法;②排查教學活動過程中產生的問題,根據問題擬定解決方案;③課前自測,驗證擬定的方案是否有效,提升學生的思辨能力;④練習訓練,培養解題表達能力;⑤及時反饋,獲得信心.
2 制定說的方法
筆者在研究“說數學”的過程中,共經歷了以下三個階段:①自由階段,教師鼓勵學生大膽地說,但迫于教師的壓力,效果甚微;②問題階段,教師根據教學活動需要,設計系列化的問題鏈,讓學生針對問題,一個個地說思路,這種教學效果雖然不錯,但存在教師牽著學生鼻子走的嫌疑,制約了學生的自主發揮;③循序漸進階段,結合教學內容與學生的認知水平,遵循一定的規律、次序,將說數學規劃成說、議、辨、練、評,五個層次.
筆者以第三階段的“說數學”教學為例,針對“分段(復合)函數的零點”的教學,具體談談“說數學”的操作過程與方法.
2.1 說開放話題,制造認知沖突
此環節的目的在于引導學生復習零點的概念與性質,強化零點可多元表征的特性.教學中,筆者發現學生在概念的表征上存在模糊性、不靈活性、分散性與不一致性等問題.這些問題會阻礙學生的思維發展.為了幫助學生從高層次理解這些概念,教師可展開以下教學活動.
(1)設計開放話題.封閉式的問題只會禁錮學生的思維,無法達到發散學生思維的目的.本節課,教師可提出:“請大家說說對函數零點的理解.”這是一個典型的開放式問題,學生在回答過程中,思維角度會比較寬泛,在學生暢所欲言時,同伴進行補充,教師在適當的時候進行引導.若學生說對了,緊接著詢問理由;若學生說錯了,則鼓勵同伴進行修正、完善.如此群策群力,即可幫助學生建立完整的知識網絡.
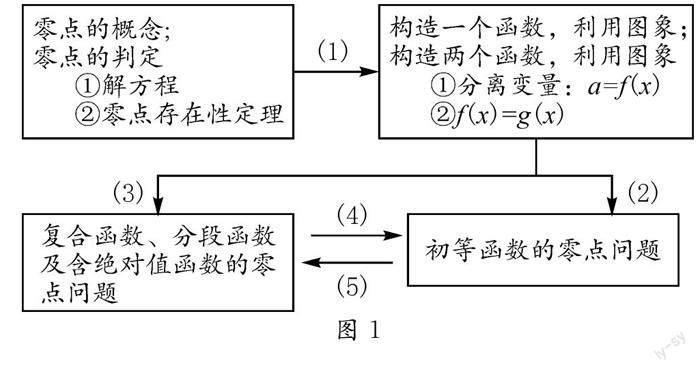
(2)制造認知沖突.每個學生對零點的認識都有所區別,教師可根據學生認知的差異性,通過一定的教學手段激發學生的認知沖突,以激活學生思維的深度與廣度.如緊扣“零點不是點”的話題,詢問:零點不是點,那是什么?它的本質是什么?有什么作用?等等.學生在對認知沖突的處理中,逐漸實現函數的零點與方程的根的互相轉化(見圖1).
2.2 議議新問題,擬定解決方案
這是一個容易被忽視的環節,而此環節卻是確定研究對象,激發學生產生學習內驅力的重要機會.首先要建立多元化的對話機制,確定研究對象.如可用:“你們在解決關于零點的問題時,曾經遇到過哪些障礙?”在學生的表達中,師生共同設計解決方案.
如學生在處理f(x)=x2-2x+12的相關問題時,運用了轉化為分段函數、整體換元等方法.在學生提出自己的困惑后,師生共同討論,并獲得解決問題的方案為:如圖1(4),將分段函數的零點問題轉化成初等函數的零點問題.若學生還不能理解這個方法,可例舉:已知,f(x)=|x|,g(x)=x2-2x+12,分別求f(g(x))與g(f(x)).
通過上述問題的解決,學生弄清楚了初等函數的零點問題是怎么變成復合分段函數的零點問題.
2.3 辨析新材料,驗證解題方案
數學教學并不純粹是解題教學,而是數學思想方法的教學.“說數學”說的是思維,到底該用怎樣的方式來辨析新材料,驗證解題方案呢?
首先,在新材料的選擇上,可考慮以下幾個方面:①可用零點相關知識來解釋、分析并解決這個材料;②材料需有新意;③材料要有明確的針對性.其次,在話題的選擇上,可從以下流程出發:課前自測、展示錯誤、錯題歸因、思考對策、完善解題.再次,在話題的引領上可提出:你用了哪些方法?為什么選擇這種方法?還有其他方法嗎?這些解題方法錯在哪兒?等等.學生親歷思考、辨析過程,可獲得思維的升華.
本節課,筆者選擇了以下材料:
(1)已知函數f(x)=2|x|,x≤0,|lg x|,x>0,那么函數g(x)=2f2(x)-3f(x)+1有幾個零點?
(2)函數f(x)=|ln x|,如果g(x)=f(x)-ax在區間(0,4)上存在三個零點,那么實數a的取值范圍是什么?
(3)若函數f(x)滿足以下幾個條件:①定義域為R;②x∈R,均有f(2+x)=f(x);③x∈[-1,1]時,f(x)=1-|x|,則方程f(x)=12log2|x|在區間[-3,5]上有幾個解?
以第(2)個材料為例,從多角度進行“說數學”,以培養學生思維的發散性與廣闊性.
師:針對第(2)個材料,你們會選擇怎樣的解題方法?并說說理由.
生1:構造h(x)=ax,分析函數h(x)與f(x)=|ln x|這兩個函數的圖象(過程略).
生2:也可以將方程變形為a=|ln x|x,令h(x)=|ln x|x=ln xx,1≤x<4,-ln xx,0<x<1.求導,然后根據h(x)的圖象來解決問題(過程略).
師:還有沒有其他方法?
生3:函數g(x)在(0,1)上必然有一個零點.若將問題轉化成g(x)在(1,4)上有兩個零點,令h(x)=ln x-ax,則h′(x)=1x-a.當a≤0時,h′(x)>0在(1,4)上恒成立,h(x)最多只有一個零點,因此可排除.當a>0時,h′(x)的零點為x=1a,此時分0<1a≤1,1a≥4與1<1a<4三種情況進行分析,最終解得ln 22<a<1e.
師生都為生3的解題思路喝彩.觀察以上解題思路,會發現區間端點特別容易被忽略掉,但學生依然能依靠自主分析完善解題過程.
2.4 練典型例題,培養表述能力
因思維水平的差異,學生的表述能力也有較大差異.為了讓學生能想得明白、說得清楚,教師可引導學生通過例題訓練、小組交流、同伴互評等方式檢驗學習成效.如本節課,筆者安排了以下例題進行教學:
(1)已知函數f(x)=x2-2x+1,x>0,x+1,x≤0,如果關于x的方程f2(x)-af(x)=0有五個不同的實數解,那么a的取值范圍是什么?
(2)若f(x)是偶函數,其定義域為R,當x∈[-2,0]時,f(x)=12x-1,如果在區間(-2,6]上關于x的方程f(x)-loga(x+2)=0(a>1)存在三個不同的實數根,那么a的取值范圍是什么?
這是兩道關于零點問題的典型例題,學生在這兩題的探究過程中,交流合作,最后獲得統一結論.筆者要求學生將自己的解題思路、過程與方法分享給大家,如此不僅鍛煉了學生的口頭表達能力,還讓學生在表達的過程中捋清了自己的思路,完善對知識的認知.
2.5 評教學反饋,增強解題信心
及時反饋評價是教學活動不可或缺的一個環節,同一節課,從不同價值觀角度出發,會有不一樣的評價方式.而不同的評價又會帶領學習者朝著不同的方向前進.從教學的時效性出發,回顧與反饋可結合在一起用“說數學”的方式進行.評價方式可多層次、多角度、多元化與多樣化.除師生的評價以外,還可吸納更多外界人士參與到評價中來,以擴大評價元,提高評價效果,增強學生的解題信心.
總之,師生、生生以及生本的“說數學”過程,是多層次的對話過程,也是多維度的思考過程.學生在交流中反饋,又在反饋中交流,最終獲得思維的發展與能力的提升,為數學核心素養的形成奠定堅實的基礎.

