一道導(dǎo)數(shù)壓軸題的“異構(gòu)”妙解
湖北省荊門市龍泉中學(xué) (448000)
范明輝
一、試題呈現(xiàn)
(2022年第七屆湖北省高三調(diào)研模擬考試第22題)已知函數(shù)f(x)=xex-1,g(x)=a(lnx+x).
(1)若不等式f(x)≥g(x)恒成立,求正實數(shù)a的值;(2)證明:x2ex>(x+2)lnx+2sinx.
二、試題分析
本題屬于探索創(chuàng)新情境,以指數(shù)函數(shù)和對數(shù)函數(shù)為載體,考查導(dǎo)數(shù)在不等式恒成立求參數(shù)值的問題以及證明不等式的問題中的應(yīng)用,涉及到函數(shù)的單調(diào)性、極值、最值等知識,對學(xué)生的數(shù)學(xué)運算能力、邏輯推理能力以及分類討論的思想,考查理性思維和數(shù)學(xué)探索的學(xué)科素養(yǎng).
三、異構(gòu)妙解
思路分析:第(1)問,將函數(shù)表達(dá)式代入可得xex-a(lnx+x)-1≥0恒成立,對代數(shù)式“xex”進(jìn)行朗博變形可得xex=elnx·ex=ex+lnx,結(jié)合導(dǎo)數(shù)問題中常用的切線不等式ex≥x+1,可構(gòu)造為[ex+lnx-(lnx+x)-1]+(1-a)(lnx+x)≥0,易知前部分ex+lnx-(lnx+x)-1≥0,而余量函數(shù)y=lnx+x在(0,+∞)上單調(diào)遞增,且值域為(-∞,+∞),故系數(shù)1-a=0,即a=1.
注:所謂“朗博變形”是指利用指數(shù)運算和對數(shù)運算法則,將形如aex(a>0)代數(shù)式中ex的系數(shù)a變形成elna,進(jìn)一步將aex變形成aex=elna·ex=ex+lna.這種變形技巧被稱為“朗博變形”,通常搭配母函數(shù)y=ex-x-1(即利用函數(shù)y=et及其在t=0處的切線y=t+1得到的切線不等式et≥t+1,將不等式移項得到母函數(shù)y=et-t-1)進(jìn)行異構(gòu)配湊,配湊的結(jié)果即aex=ex+lna=ex+lna-(x+lna)-1+x-lna+1,這里的代數(shù)式ex+lna-(x+lna)-1與et-t-1是同構(gòu)的,都是非負(fù)的,至于多出來的余量x-lna+1需結(jié)合具體的題目進(jìn)行配湊.
第(2)問,將待證不等式移項變形得x2ex-xlnx-2lnx-2sinx>0,觀察到前兩項中含公因式x,提取之后同(1)進(jìn)行朗博變形得x[ex+lnx-(lnx+x)-1]+x2+x-2lnx-2sinx>0,對于后面出現(xiàn)的x2-2lnx項,可以聯(lián)系常用的切線不等式x-1≥lnx,將其變形為x2-1-lnx2≥0,此時還剩下x+1-2sinx,結(jié)合正弦函數(shù)的性質(zhì)可知x-sinx≥0,1-sinx≥0,則待證不等式轉(zhuǎn)化為證明x[ex+lnx-(lnx+x)-1]+x2-1-lnx2+x-sinx+1-sinx>0.這種將原復(fù)雜函數(shù)通過恒等變形轉(zhuǎn)化為多個不同的簡單函數(shù)的構(gòu)造方法就是異構(gòu).
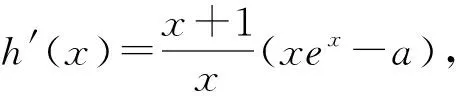
當(dāng)a=1時,?x0>0,使得x0+lnx0=0,∴φ(x)在(0,x0)上為負(fù),在(x0,+∞)上為正.∴h(x)在(0,x0)上單調(diào)遞減,在(x0,+∞)上單調(diào)遞增.∴h(x)≥h(x0)=0,符合題意.
當(dāng)a>1時,?x1>x0,使得x1+lnx1=lna,∴φ(x)在(0,x1)上為負(fù),在(x1,+∞)上為正.
∴h(x)在(0,x1)上單調(diào)遞減,在(x1,+∞)上單調(diào)遞增.∴h(x1) 當(dāng)a<1時,?x2 (2)即證x[ex+lnx-(lnx+x)-1]+x2-1-lnx2+x-sinx+1-sinx>0,記F(x)=ex-x-1(x∈R),則F′(x)=ex-1,∴F(x)在(-∞,0)上單調(diào)遞減,在(0,+∞)上單調(diào)遞增.∴F(x)≥F(0)=0,即ex-x-1≥0,∴ex+lnx-(lnx+x)-1≥0,當(dāng)且僅當(dāng)x0+lnx0=0時取等號. 以上解法中,第(2)問的異構(gòu)解法尤為美妙,主要依托于常用的不等式ex-x-1≥0,x-1-lnx≥0以及三角函數(shù)的性質(zhì),通過對待證不等式進(jìn)行恒等變形,化歸為證明熟悉的不等式,將未知向已知轉(zhuǎn)化.但是,異構(gòu)法難于構(gòu)造,難于轉(zhuǎn)化,這需要在平時多加訓(xùn)練,掌握常用的不等式.一旦熟練掌握異構(gòu)法,解決導(dǎo)數(shù)中的不等式證明問題及恒成立問題將會顯得容易.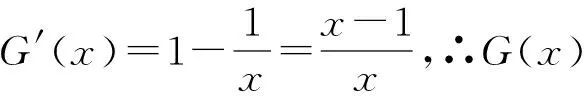
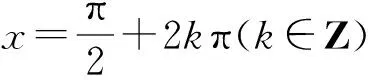
四、小結(jié)反思

