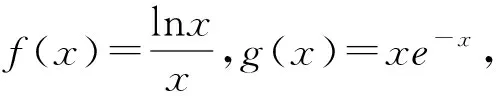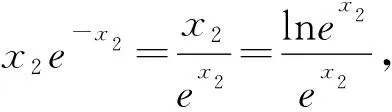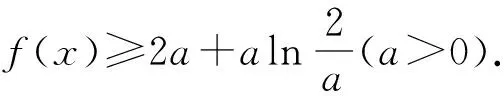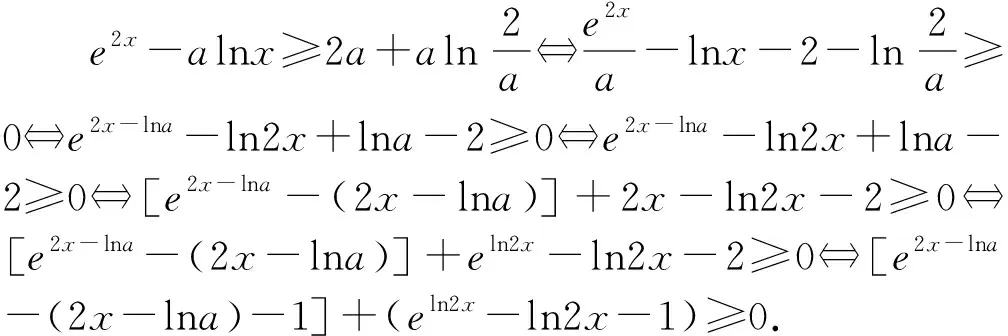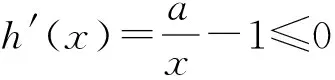巧用同構思想妙解一類指對混合壓軸題
福建省永春第一中學 (362601)
劉文哲 張隆億
對方程或不等式進行變形轉化,使其左側和右側具有相同的結構形式,再通過構造單調函數處理.對于具有混合指數對數的問題,通常可以通過指數和對數的相互變換實現局部同構.問題可以轉化為相應函數單調性或函數最值,這大大降低了計算和求解(證明)的難度.它是數學核心素養如邏輯推理和數學建模的有效媒介,受到高考命題者的青睞.本文提出了指數與對數等式(不等式)的同構方法,并對含指數對數壓軸問題的同構解法進行了梳理.
一、同構的常見方法
1 利用x=lnex,x=elnx(x>0)進行冪指、冪對轉換同構
2 對等式、不等式兩邊取指數、對數進行同構
2.1 積型aea 1 命題手法1:運用同構思想,轉化為h(m(x))形式的式子. 對函數式同構轉化,根據結構特點,構造一個對應的函數y=h(x),將涉及函數式h(m(x))問題,轉化為這兩個函數y=h(x),y=m(x)的最值,達到簡化難度的目的.這類試題通常以參數范圍和不等式證明等形式進行考查. 2 命題手法2:運用同構思想,轉化為h(m(x1))=h(n(x2))形式的等式. 對等式兩邊同構轉化,構造函數y=h(x),等式可以轉化為h(m(x1))=h(n(x2)).若函數y=h(x)是單調的,等式可簡化為m(x1)=n(x2),從而簡化等式,化繁為簡.試題常以化簡求值,變量的最值等形式進行考查. 例2 (2021孝感期末)若x0為函數f(x)=e2lnx+x-2+lnx-2的一個零點,則e2-x0+lnx0的值為. 解析:根據題意,令f(x)=0,得e2lnx+x-2=2-lnx,兩邊取對數可得2lnx+x-2=ln(2-lnx),即lnx+x-(2-lnx)=ln(2-lnx),得到lnx+x=ln(2-lnx)+(2-lnx),設h(x)=x+lnx,x∈(0,+∞),則h(x)=h(2-lnx).結合h(x)的單調性可得x=2-lnx,由函數零點的定義可得x0=2-lnx0,所以e2-x0+lnx0=elnx0=x0+2-x0=2. 3 命題手法3:運用同構思想,轉化為含有h(m(x1))及h(n(x2))的不等式 對不等式的兩邊進行同構變換,構造一個對應的函數y=h(x),將原不等式可以轉化為含有h(m(x1))及h(n(x2))的不等式,以達到簡化不等式結構的目的.試題通常以不等式證明和參數范圍等形式進行考查. 3.1 若函數y=h(x)是單調的,則不等式h(m(x1)) 例4 (2020山東21節選)若aex-1-lnx+lna≥1,試求實數a的范圍. 解析:將aex-1進行同構變形為ex-1+lna,則不等式aex-1-lnx+lna≥1可整理為ex-1+lna+lna-1≥lnx,兩邊同加x可得ex-1+lna+lna+x-1≥lnx+x,即ex-1+lna+lna+x-1≥lnx+x=elnx+lnx.令h(x)=ex+x,則h(x-1+lna)≥h(x),可由函數h(x)單調性,得x-1+lna≥x,即lna≥lnx-x+1.利用導數工具可得函數y=lnx-x+1的最大值為0,所以a的取值范圍為[1,+∞). 例5 若函數f(x)=lnx-x+1,函數g(x)=axex-4x,a>0,證明:g(x)-2f(x)≥2(lna-ln2). 解析:由axex=ex+lnx+lna可知要證的不等式axex-2x-2lnx-2lna≥2-2ln2可化為ex+lnx+lna-2(x+lnx+lna)≥eln2-2ln2.設h(x)=ex-2x,則h(x+lnx+lna)≥h(ln2).該不等式證明等同于證明函數h(x)的最小值h(ln2),利用函數h(x)的單調性加于驗證即可. 3.2 結合轉化后不等式h(m(x1))+h(n(x2))<0,不等式的證明可h(x)<0推出.含有雙元x1、x2不等式證明,可化歸為函數y=h(x)的值域求解,達到化繁為簡的目的. 3.3 結合m(x1) 例7 (2022泉州質檢二)已知函數f(x)=ax-ex,?x∈(1,+∞),f(x) 解析1:由alnx+a-ex=a(lnx+1)-elnx+1,得f(x) 簡而言之,能直接使用同構的混合指數和對數的導數試題不多.在許多情況下,需要用指數和對數同構技巧,嘗試轉換為三種常見的同構形式.解決這類含有指數對數導數試題的關鍵是同構變換,進而構造一個對應函數,將問題轉化為函數單調性或函數范圍,化難為易,突破解題的障礙點.這類含指數對數壓軸題同構解法事實上就是數學建模中建模、解模的過程.在這類導數壓軸題求解過程中引入了建模方法,教師應引導學生從不同的角度思考,對同一個問題建立不同的數學解模型,讓學生從多個角度學習,尋找不同的問題解決方法,培養創新意識,使他們在面對復雜的函數和導數問題時能夠有章可循,一方面提高學生的數學建模技能,另一方面使學生養成有意識地運用數學建模思想解決問題的習慣,往往能達到事半功倍的效果.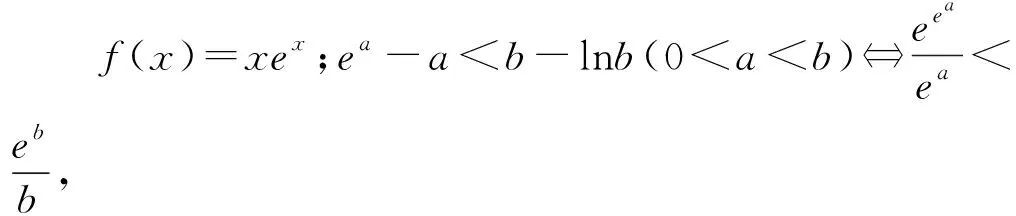
二、常見命題手法