巧構直線方程 讓函數不等式放縮有“度”
浙江省安吉縣高級中學
林蘭蘭
函數不等式的放縮問題不僅是學生學習的難點,更是近年來各地高考命題的一個熱點.其思維的獨特性、解題手段的靈活性、知識內容的綜合性等特點,在對形成學生理性思維、科學精神和促進學生個人智力發展的過程中發揮著重要作用,但也使不少學生望而卻步.筆者選取構造直線方程的角度談談如何把握函數不等式放縮的“度”.
1 構造垂線放縮

(1)當a=0時,判斷函數f(x)的奇偶性;
(2)若f(x)≥4x-6恒成立,求a的取值范圍;
(3)設b∈R,若關于x的方程f(x)=b-8有實數解,求a2+b2的最小值.
解析:(1)(2)略.
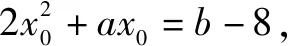

點評:本題從a2+b2的結構出發,聯想到原點與點(a,b)的距離的平方.點(a,b)的軌跡是什么?從已知條件出發,構造兩條直線方程,巧妙地利用“垂線段最短”,使問題獲解.
2 構造切線放縮
例2(2020年高考全國卷Ⅰ第21題)已知函數f(x)=ex+ax2-x.
(1)當a=1時,討論f(x)的單調性;

解析:(1)略.

①當x=0時,得a∈R.
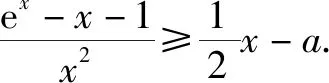



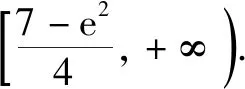

3 構造割線放縮
例3(2021年高考全國卷Ⅰ第22題)已知函數f(x)=x(1-lnx).
(1)討論f(x)的單調性;
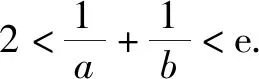
解析:(1)略.

對x1進行割線放縮:作直線y=x,其與直線y=m交于點(m,m),而y=m與y=f(x)交于點(x1,m),于是x1 對x2進行切線放縮:作y=f(x)在(e,0)處的切線:y=-x+e,它與直線y=m交于點(e-m,m),故x2 從而x1+x2 點評:本題以直代曲,抓住函數在特定范圍內區間端點特征,對x1進行割線放縮,對x2進行切線放縮,合理把握了放縮的“度”.這種放縮方法,需要充分理解函數的圖象性質,特別是函數的單調性和凹凸性.它不同于常見的放縮手段,讓學生有耳目一新之感,這對學生數學思維的拓展大有幫助. (1)求f(x)在x∈(0,1]上的最大值; (2)若g(x)≤0對任意的b∈[a,+∞)及x∈(0,1]恒……4 構造隱性直線放縮


