基于高考試題的數(shù)學課堂教學情境創(chuàng)設實踐研究

賈志國

【摘要】教育改革發(fā)展推動高考內容優(yōu)化，高考內容逐漸走向現(xiàn)實社會發(fā)展需要，而不再一味強調學生數(shù)學學習技巧掌握情況，高考對學生綜合素質評價的作用愈加顯現(xiàn).另外，“中國高考評價體系”“一核”“四層”“四翼”內容的確定，推動高考教育改革不斷落實完善，關于高考相關內容的研究備受重視.如何基于數(shù)學學科情境設置，再現(xiàn)學科理論情景或反映現(xiàn)實社會問題，推動學生綜合素質提升，成為高中數(shù)學學科教學不容忽視的重點.

【關鍵詞】高中數(shù)學；高考試題；課堂教學

情境之于高考，既是價值實現(xiàn)的引領、素養(yǎng)導向的載體、能力體現(xiàn)的工具，也是知識考查的形式，是落實學生綜合素質教育的有效手段.

筆者以高考評價體系為依據(jù)，以高中數(shù)學學科特點為前提，創(chuàng)設學習再現(xiàn)情境、學習關聯(lián)情境、綜合聯(lián)想情境、拓展遷移情境、模型識別情境等高考數(shù)學試題情境，并基于具體試題做出解釋說明.為盡量保證試題情境能夠準確、有效發(fā)揮載體作用，高考數(shù)學試題情境的創(chuàng)設應遵循真實性、公平性、一致性和簡潔性原則.

1 學習再現(xiàn)情境的創(chuàng)設

學習再現(xiàn)情境的創(chuàng)設，以學生已學課程體系內的情境型材料為主，此類材料內部關聯(lián)性為學生所熟知，相應情境創(chuàng)設由學生直接回憶再現(xiàn)即可.簡言之，就是讓學生將已有知識、方法與試題進行關聯(lián).此情境創(chuàng)設方法相對簡單，主要是對“四層”的考查，即對學生核心價值、學科素養(yǎng)、關鍵能力、必備知識的考查.

例1 在（1）a1+a3= b2；（2）b4= a4； （3）S5=-25，這3個條件中任選1個，在下列問題中進行補充說明，假設問題中存在y值，請進行求解，假設不存在，請說明理由.

設等差數(shù)列｛bn｝中，前n項之和為Sn，｛an｝為等比數(shù)列，，a1= b5，a2=3，a5=-81，y是否存在才會讓Sy＞Sy+1且Sy+1＜Sy+2成立？

此例題考查“等差數(shù)列與等比數(shù)列”相關情境型課程知識，相應的情境創(chuàng)設依托等差和等比數(shù)列通項公式、前n項和公式、等差和等比數(shù)列“基本量法”“擬真推證法”等進行，而此部分內容均為學生已學內容.

因此，此例題為學習再現(xiàn)情境的創(chuàng)設，在學生基礎知識考查的基礎上，對學生的思維能力、探索能力、問題解決能力等進行培養(yǎng)，也對學生等差等比數(shù)列相關知識進行進一步的鞏固復習.

2 學習關聯(lián)情境的創(chuàng)設

學習關聯(lián)情境的創(chuàng)設，也以學生已學課程體系內的情境型材料為主，但學生對此類材料的內部關聯(lián)性了解并不完全，或學生對此的熟悉程度有所欠缺，故而要創(chuàng)設此類情境，既需要借助學生已掌握的知識內容，也需要學生發(fā)動腦內知識體系，通過回憶將試題與知識聯(lián)想連接起來.此情境創(chuàng)設中復雜程度更高，也是對“四層”的考查.

例2 有一球面半徑為2cm，該球面上有4點O、P、Q、M，其中OP、OQ、OM三條線之間為兩兩垂直關系，試求S△OPQ+S△OQM+S△OMP的最大值.

這一例題中涉及的情境型材料包括立體幾何的初步學習、基本不等式等，相應的情境創(chuàng)設所依托的知識和方法則涉及較為廣泛，包括直線和平面之間的垂直關系、長方體棱長和長方體外接球半徑的關系、三元基本不等式、基本不等式求最值的方法、步形解題法等，而此部分內容與方法均為典型的回憶再現(xiàn).

但這種情境創(chuàng)設過程中需注意以下兩點：其一，三元基本不等式與三角形面積之和的最大值之間關聯(lián)性并不明顯；其二，長方體構造與題目具體給出的條件之間也無明顯關聯(lián)性.

以此為前提，就需要創(chuàng)設學習關聯(lián)情境，基于模型“求S=12（AB.AC+AC.AD+AD.AB）的最大值”構建關系式OP2+OQ2+OM2=16，借助“基本不等式最值計算”完成題目的聯(lián)想，進而才能夠完成情境創(chuàng)設.

而這樣的情境創(chuàng)設，在培養(yǎng)學生想象聯(lián)想、建模思維、邏輯能力、解題能力等方面都有價值，也便于學生鞏固和學習三元基本不等式等知識.

3 綜合聯(lián)想情境的創(chuàng)設

綜合聯(lián)想情境的創(chuàng)設，仍舊以學生已學課程體系內的情境型材料為主，但材料表現(xiàn)形式、材料內含知識、方法之間的關聯(lián)，相對隱性，來源于學生已獲得知識或體驗.

因此，此情境的創(chuàng)設需要學生對相關知識有較明確的整體把握、等價轉換和即景聯(lián)想.此情境創(chuàng)設也是對“四層”的考查.

例3 現(xiàn)有一橢圓A，與x軸的交點為M1（-1，0），M2（1，0），與A交于點O、P的直線過M2，若|OM2|=2|M2P|，|OP|=|PM1|，則M的方程式是（? ）

（A）x22+y2=1.??? （B）x23+y22=1.

（C）x24+y23=1. （D）x25+y24=1.

此例題情境型材料包括橢圓的標準方程和幾何的性質兩部分，材料所隱含知識直接來源于學生已有知識積累，但與橢圓定義及表達式相關的知識取決于學生更深層次的知識儲備，故而解此題時需創(chuàng)設綜合聯(lián)想情境.

具體來講，學生充分掌握了橢圓的定義，有效關聯(lián)到|OM2|=2|M2P|，|OP|=|PM1|，就可由此等價轉化得到新的條件|OM2|=a，|PM2|=a2，|OM1|=a，|PM1|=3a2.基于此，要求出a值，再結合|M1M2|=2，就能即景聯(lián)想到余弦定理，借助△OM1M2和△PM1M2中的互補角∠OM2M1和△PM2M1來完成解題.

這樣的情境創(chuàng)設對于培養(yǎng)學生數(shù)學思維、建模、運算等能力，引導學生進一步扎實知識功底有顯著意義.

4 拓展遷移情境的創(chuàng)設

拓展遷移情境的創(chuàng)設，前提條件同樣是已學課程體系內的情境型材料，但材料呈現(xiàn)方式和試題題目之間的關聯(lián)性不高，對應情境創(chuàng)設需基于對材料的創(chuàng)造性解讀、轉換及遷移來完成，考查內容也為“四層”.

例4 已知函數(shù)f（y）=（y-1）ay，

（1）試求出f（y）的單調區(qū)間；

（2）當m>n>0時，試證明nam+m>man+n.

此例題設計中，問題（1）以學習再現(xiàn)情境為前提，基于對學生函數(shù)單調區(qū)間、導數(shù)與函數(shù)單調性關系等基礎知識考查的同時，旨在培養(yǎng)學生的數(shù)學運算和問題解決能力.

問題（2）則重在考查知識點“導數(shù)在函數(shù)中的應用”，基于函數(shù)單調性與題目條件之間的不明顯關聯(lián)，達到情境創(chuàng)設目的，需要學生在解題中基于函數(shù)背景，將不等式轉化為函數(shù)大小求解或比較，進而完成對表達式的am-1m>an-1n證明.

此時，學生所需要解決的問題就被轉化為證明函數(shù)g（y）=ay-1y在（0，+SymboleB@）單調遞增.

這一情境除了培養(yǎng)學生建模、求解等方面的能力，也重在培養(yǎng)學生的創(chuàng)新聯(lián)系能力，讓學生能夠更靈活地融合知識，解答題目.

5 模型識別情境的創(chuàng)設

模型識別情境的創(chuàng)設則與學習再現(xiàn)情境、學習關聯(lián)情境、綜合聯(lián)想情境、拓展遷移情境的創(chuàng)設有極大區(qū)別，其中主要表現(xiàn)在創(chuàng)設的前提和基礎，前者以現(xiàn)實社會中反映社會大眾現(xiàn)實需要的衣、食、住、行、健康、教育、休閑、自我提升等密切相關，后者則以已學課程體系內的情境型材料為主.

模型識別情境涉及的知識、方法、模型構建等旨在基于學生的知識儲備，將數(shù)學知識直觀化、生活化，以期解決現(xiàn)實問題.

模型識別情境為相對簡單的生活性、實踐性情境，便于學生產(chǎn)生“生活處處有數(shù)學”的知識現(xiàn)實應用意識，讓學生堅定數(shù)學學習信念，引導學生學會基于數(shù)學知識解決生活問題.

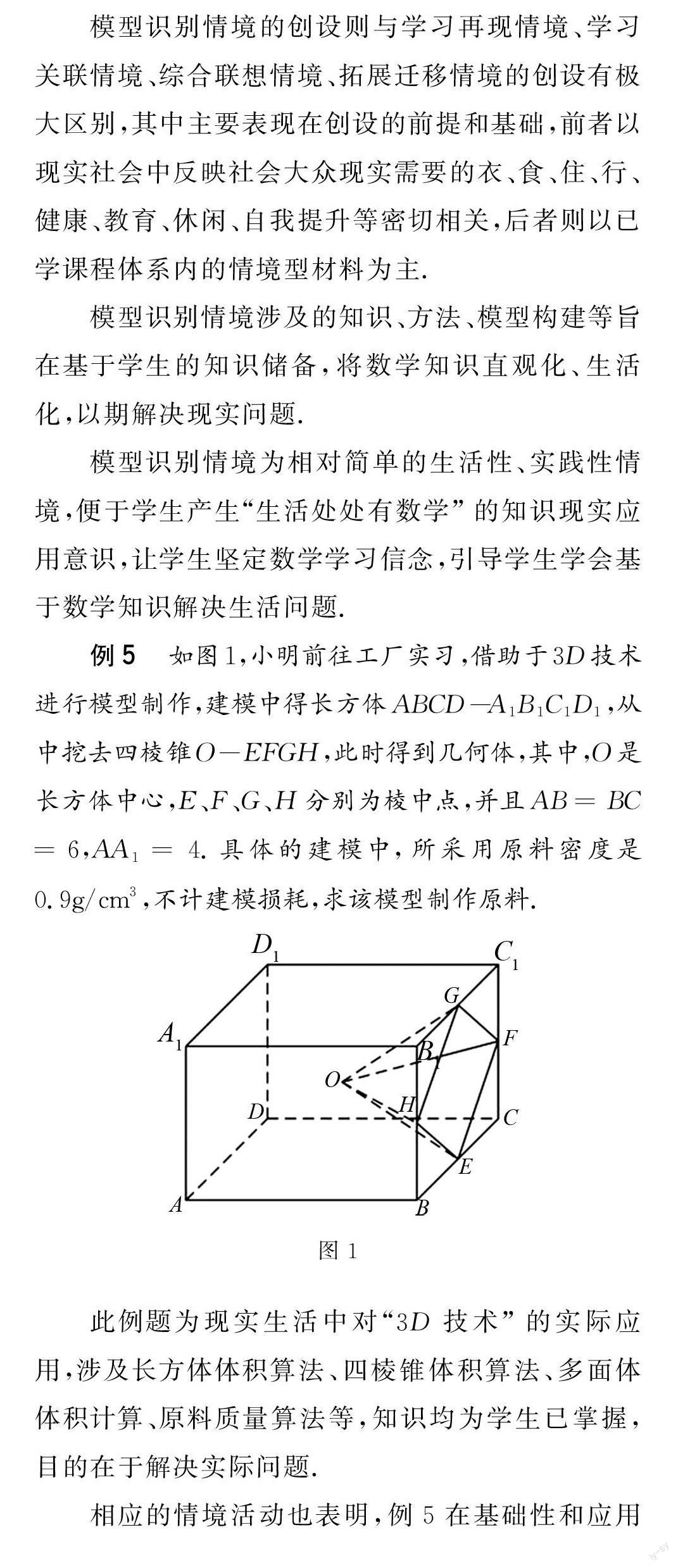
例5 如圖1，小明前往工廠實習，借助于3D技術進行模型制作，建模中得長方體ABCD-A1B1C1D1，從中挖去四棱錐O-EFGH，此時得到幾何體，其中，O是長方體中心，E、F、G、H分別為棱中點，并且AB=BC=6，AA1=4.具體的建模中，所采用原料密度是0.9g/cm3，不計建模損耗，求該模型制作原料.

圖1

此例題為現(xiàn)實生活中對“3D技術”的實際應用，涉及長方體體積算法、四棱錐體積算法、多面體體積計算、原料質量算法等，知識均為學生已掌握，目的在于解決實際問題.

相應的情境活動也表明，例5在基礎性和應用性的層次上考查了數(shù)學應用、數(shù)學探索等學科素養(yǎng)，空間想象、運算求解等關鍵能力，以及長方體、四棱錐的體積公式等必備知識.

6 結語

總之，教育改革發(fā)展推動考試體制改革，教育越來越強調知識的生活化應用和現(xiàn)實需要滿足，高考題目設計也更為重視情境的創(chuàng)設.

基于此，教師要培養(yǎng)學生的數(shù)學問題解決能力，前提就是熟悉當前的考試試題情境創(chuàng)設類型，并系統(tǒng)化將這些內容應用于課題教學實踐，培養(yǎng)學生的情境應用能力，讓學生能夠準確判斷試題情境的類型、前提、方法內容與題目條件的關聯(lián)深度等，以期能夠及時完成試題解答，既提升學生的知識應用能力，落實高考評價體系的“一核四層四翼”，也進一步實現(xiàn)現(xiàn)代教育的綜合發(fā)展，為打造更多全面型人才奠定現(xiàn)實基礎.

參考文獻：

[1]劉子麗，謝發(fā)超.高考數(shù)學試題情境分析與教學建議——以2020年高考數(shù)學全國卷Ⅱ理科為例[J].教育科學論壇，2022（04）：40-42.

[2]陳小波.幾何特征：高考“情境化試題”解題思路的來源——以2021年全國數(shù)學高考卷Ⅰ第19題為例[J].中學教研（數(shù)學），2021（09）：43-46.

[3]羌達勛.基于“一核四層四翼”高考評價體系的試題情境分析——以2021年高考模擬演練數(shù)學卷為例[J].中學數(shù)學月刊，2021（06）：59-61.

[4]劉太濤，鄭傳遠.高考數(shù)學三類情境下的試題評析及教學建議——以2020年高考數(shù)學試題為例[J].中學數(shù)學研究（華南師范大學版），2021（08）：45-47.

[5]謝榕平.高考評價體系下以情境為載體的數(shù)學試題及備考策略研究[J].理科考試研究，2021，28（01）：2-4.

[6]張景信，廖光及，林劍.情境視角下的高考數(shù)學試題分析與思考——以2017-2019年全國數(shù)學Ⅰ卷理科為例[J].理科考試研究，2020，2）：2-5.