核心素養(yǎng)視域下學(xué)生運算能力培養(yǎng)策略探究

馬萬雄

摘 要：運算能力是小學(xué)階段學(xué)生學(xué)習(xí)數(shù)學(xué)必須掌握的一項關(guān)鍵技能，也是他們今后學(xué)習(xí)更高層次知識時不可或缺的基礎(chǔ)。“核心素養(yǎng)”是近年來提出的理念，逐漸成為教育教學(xué)中關(guān)注的熱點，把核心素養(yǎng)融入具體的學(xué)科教學(xué)中是一種大的趨勢，而運算能力則屬于數(shù)學(xué)核心素養(yǎng)。新一輪基礎(chǔ)教育的不斷改革要求教師不僅要向?qū)W生傳輸教材中“加減乘除”等基礎(chǔ)的運算知識，更要注重對學(xué)生運算技能的訓(xùn)練和培養(yǎng)，要讓學(xué)生憑借自己的能力獨立進(jìn)行運算，促進(jìn)其運算能力的形成和穩(wěn)步提升，將學(xué)生培養(yǎng)成為“知識+技能+素養(yǎng)”型的人才。

關(guān)鍵詞：核心素養(yǎng);運算能力;培養(yǎng)策略

中圖分類號：G623.5?? 文獻(xiàn)標(biāo)識碼：A?? 文章編號：1673-8918（2022）16-0090-05

一、 引言

在現(xiàn)階段的小學(xué)數(shù)學(xué)教學(xué)中還存有一些問題，雖然大部分教師都能意識到運算教學(xué)的重要性，但是實際的效果并不盡如人意。教師所設(shè)計的運算習(xí)題太過單一，內(nèi)容有時簡單、有時過難，很少考慮本班學(xué)生的實際情況和運算水平，過于簡單的運算對學(xué)生的思維起不到太大的推動作用，而過難的運算題又會挫傷學(xué)生主動計算的積極性。可見教師在設(shè)計運算練習(xí)題時沒有充分依據(jù)學(xué)生的學(xué)情，導(dǎo)致運算練習(xí)題脫離了學(xué)生的實際，學(xué)生也只能機械地應(yīng)付訓(xùn)練。長此以往，他們的運算技能就難以得到提升和強化，更別提核心素養(yǎng)的形成。因此，為了改變這種現(xiàn)狀，教師必須科學(xué)安排運算訓(xùn)練的內(nèi)容。筆者結(jié)合自身的實踐，在文章提出了以下幾點核心素養(yǎng)視域下學(xué)生運算能力培養(yǎng)策略，希望能夠為其他教師提供借鑒與參考。

二、 學(xué)生運算能力的現(xiàn)狀及問題分析

（一）運算技能方面

1. 口算能力有待提升，學(xué)生運算速度較慢

眾所周知，口算是進(jìn)行筆算的基礎(chǔ)，只有掌握較強的口算能力才能在筆算中形成清晰的思路;而筆算是口算能力的具體體現(xiàn)，雖然這兩種計算方式不同，但其中的算理卻相融。學(xué)生掌握一定的口算能力后他們的筆算速度才不會受影響，還能提高筆算的準(zhǔn)確度。縱觀現(xiàn)狀，部分學(xué)生的口算能力有待提升，很少有學(xué)生能夠在短短的五分鐘內(nèi)順利完成50道運算練習(xí)題，他們的整體運算速度比較緩慢，而且運算結(jié)果的準(zhǔn)確性也不夠理想。除了口算能力薄弱以外，學(xué)生的估算意識也不強，在筆算的過程中難以做到靈活運用，從而造成運算速度、運算正確率普遍不佳。

2. 缺乏簡便運算意識，受思維定勢的影響

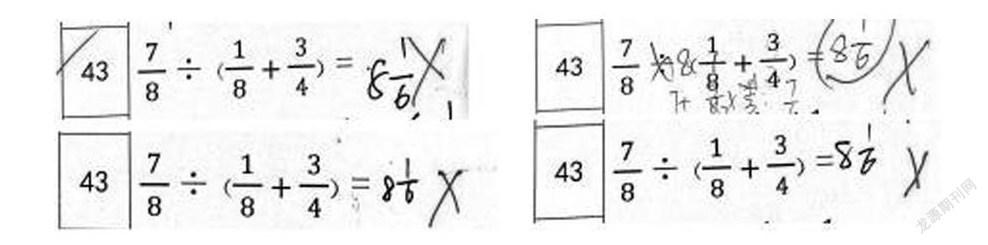
簡便運算是指將比較復(fù)雜的運算過程簡化為相對簡單的運算。如若學(xué)生形成一定的簡算意識，那么他們在解決實際問題時就能把復(fù)雜的步驟變得簡單，從而提高實際運算的速度，同時還能提高學(xué)生思維的靈活性。但在目前的運算學(xué)習(xí)中存在著這樣的問題，部分學(xué)生往往不經(jīng)過思考，機械地使用學(xué)過的運算定律來計算，這不僅說明他們?nèi)狈啽氵\算的意識，而且還受到思維定勢的深刻影響。比如，在遇到下面這道運算題時，許多學(xué)生都會受定勢思維的影響，片面地認(rèn)為這道題應(yīng)該使用“除法分配律”來進(jìn)行運算。

學(xué)生在運算方面犯的錯誤“如出一轍”，在復(fù)雜運算題面前往往不能進(jìn)行合理的簡算，這說明他們的簡便運算意識比較缺乏，還不能恰當(dāng)?shù)卦诨旌线\算中使用所學(xué)的運算定律，而且極容易受到思維定勢的影響。

（二）非智力因素方面

1. 運算教學(xué)的單一枯燥，學(xué)生難以形成運算興趣

對于數(shù)學(xué)教師而言，運算教學(xué)是不可忽視的一個重點;對于學(xué)生來說，對運算知識的學(xué)習(xí)過于單調(diào)，缺乏對運算學(xué)習(xí)的強烈興趣，造成學(xué)生進(jìn)行運算的積極性普遍不高。部分教師在運算教學(xué)過程中往往采取單純“口授”的形式，過于突出對某個運算定律的“講”，這種枯燥的講解逐漸磨滅了學(xué)生原本的熱情，讓他們覺得運算學(xué)習(xí)是無味的，從而對數(shù)學(xué)運算題沒有太大的興趣。可以說教師怎樣“教”就影響學(xué)生怎樣“學(xué)”，要想促進(jìn)學(xué)生運算興趣的形成和提高，教師必須改變自身“教”的方法，比如適當(dāng)?shù)厝谌胗嬎阌螒颉?gòu)建一定的趣味運算情境等，以此來改變學(xué)生以往對運算知識學(xué)習(xí)的消極態(tài)度。

2. 運算學(xué)習(xí)的態(tài)度不正，未形成計算的自主意識

具備良好的態(tài)度對運算學(xué)習(xí)有著維持、強化的作用。對于小學(xué)階段的學(xué)生而言，學(xué)習(xí)與運算相關(guān)的知識本身就存在一定的難度，尤其是在面對比較復(fù)雜的混合運算時，他們往往表現(xiàn)出態(tài)度不正、不愿意做的消極狀態(tài)，甚至有些題目已經(jīng)出現(xiàn)過好多次，但學(xué)生就不愿意動腦去算一算，覺得反正一會兒教師就公布答案了，這說明他們還是處于思維懶惰的狀態(tài)，缺乏對問題的自主探究。

三、 核心素養(yǎng)視域下學(xué)生運算能力的培養(yǎng)策略

（一）理解運算對象

1. 理解運算意義

數(shù)學(xué)教學(xué)的目的不是讓學(xué)生習(xí)得更多知識、考取更多分?jǐn)?shù)，而是讓他們可以把所學(xué)的用到實際生活中，從而實現(xiàn)“學(xué)以致用”。因此，在運算教學(xué)中，教師可以適當(dāng)?shù)厝谌肷钪械馁Y源來開展運算訓(xùn)練，給學(xué)生呈現(xiàn)熟悉的情境。一方面，調(diào)動學(xué)生以往的認(rèn)知經(jīng)驗，促進(jìn)其對練習(xí)題的自主運算;另一方面，增添數(shù)學(xué)課的“生活味兒”，讓他們不再覺得數(shù)學(xué)課是枯燥的，從而提高他們的運算興趣。此外，在融入生活問題的過程中有利于讓學(xué)生體會到生活中處處都離不開運算，進(jìn)而體驗運算的意義，使他們形成運用數(shù)學(xué)的意識。

例如，在教學(xué)“小數(shù)乘整數(shù)”相關(guān)內(nèi)容時，為了讓學(xué)生體會到其在生活中的運用，教師安排了一個課后任務(wù)，要求家長帶著學(xué)生到超市去購買生活用品或是買菜，最后把購物小票交給學(xué)生，讓學(xué)生把自己的購物單帶到課堂上。在課上，教師鼓勵學(xué)生根據(jù)小票說一說自己買了什么、花了多少錢，并對他們進(jìn)行適當(dāng)?shù)奶釂枴煟骸拔覀兛葱埖男∑鄙厦姘鼏蝺r是3.5元，一共買了4個面包，那買面包花了多少花錢？”在問題的引領(lǐng)下，學(xué)生自主展開運算，結(jié)合以往的購物經(jīng)驗紛紛得出了不同的算法。比如，第一種算法：學(xué)生看成4個35角，計算4×35是多少，然后再換算成元的單位;第二種算法：先計算4個3元，再計算4個5角，最后加起來;第三種算法：計算4個4元，然后減去4個5角……在學(xué)生運算的過程中，他們不僅解決了實際問題，而且還感悟了算理，掌握了不同的算法，同時也感受到運算在生活中的意義，能夠達(dá)到學(xué)以致用的目的。

2. 理解運算內(nèi)容

掌握運算能力的重要前提是理解算理，只有做到明晰算理，才能使學(xué)生不斷優(yōu)化自身的算法。因此，在具體的教學(xué)中，教師應(yīng)該有意識地引領(lǐng)學(xué)生理解運算的內(nèi)容，切實培養(yǎng)學(xué)生的核心素養(yǎng)，讓學(xué)生經(jīng)過算理的過程推導(dǎo)，使其明白“為什么這么算”，從而才能做到“知其然，知其所以然”。在安排運算練習(xí)時，教師可以采用“構(gòu)建生活情境——鼓勵列算式——探究算法——解決問題”的流程，這樣學(xué)生會更容易理解運算的順序和道理。

例如，在教學(xué)“加減混合運算”時，教師可以構(gòu)建上下公交車的熟悉情境，以此來幫助學(xué)生理解算理。師：“同學(xué)們，今天早上坐公交車的時候車上有7個人，過了一站有2個人從后門下車，3個人前門上車，那么現(xiàn)在車上應(yīng)該有幾個人呢？”要想解決這個問題，學(xué)生需要減去下車的人數(shù)，然后加上后來上的人數(shù)，進(jìn)而列出相應(yīng)的算式：7-2+3。當(dāng)然，也有學(xué)生先加了上的人，后減去下的人，列出這樣的算式：7+3-2。這兩種方法都是對的，但是在計算的過程中必須按照從左往右的順序。學(xué)生都有坐公交的經(jīng)驗，在這樣的情境中他們列出算式，然后進(jìn)一步探究其中計算的步驟和順序，聯(lián)系以往的生活經(jīng)驗自然而然地明晰其中的算理，從而理解運算的內(nèi)容。

（二）掌握運算法則

1. 掌握恰當(dāng)算法

由于學(xué)生在認(rèn)知基礎(chǔ)、思維水平等方面存在著或大或小的差異，所以他們呈現(xiàn)出來的算法也有所不同。對有的學(xué)生來說，只掌握了一種算法，但是對其他的學(xué)生來說會運用更多種的算法。作為教師應(yīng)該鼓勵學(xué)生大膽嘗試用不同的方法來展開計算，讓他們選擇恰當(dāng)?shù)姆椒ǎ瑢Ω鞣N算法進(jìn)行對比、分析，從中選出最優(yōu)的方法，這樣有利于學(xué)生掌握“優(yōu)化”的思維方法，也有利于提高他們的運算能力。隨著方法的多樣化，學(xué)生的運算思維也獲得由淺至深的發(fā)展，他們的思維素養(yǎng)也會有所提升。

例如，在課上教師給學(xué)生展示了一個算式“9+4”，讓學(xué)生進(jìn)行計算，并分享自己是如何計算的，與自己的同桌交流具體的算法。如有的學(xué)生說自己是一個一個數(shù)的，從1，2，3一直數(shù)到12，13，最后得出是13;有的學(xué)生說一開始有9個，所以從9開始往后數(shù)四個數(shù)，10，11，12，13，最后得出13;還有的學(xué)生說可以先從4個小棒里拿走一個，放到9個小棒中正好湊夠10個，然后再加上剩下的3個小棒，一共是13個……學(xué)生說著自己計算9+4的方法，最后教師引導(dǎo)學(xué)生對這些方法進(jìn)行歸納、分析，說一說哪個是最優(yōu)的算法，通過分析學(xué)生普遍說出“湊十”的方法最簡單，于是教師抓住時機給學(xué)生介紹“湊十法”，幫助他們掌握恰當(dāng)?shù)乃惴ǎ⑹顾麄儗W(xué)會“優(yōu)化”的數(shù)學(xué)思維。

2. 掌握相應(yīng)法則

運算法則是小學(xué)數(shù)學(xué)教學(xué)中不可或缺的一個重要基礎(chǔ)，能讓學(xué)生的計算方法達(dá)到規(guī)范化的程度。但在目前的課堂上，教師過于注重對運算技能的訓(xùn)練，忽視了引領(lǐng)學(xué)生對法則進(jìn)行歸納，導(dǎo)致學(xué)生對運算法則的掌握程度不深，進(jìn)而影響他們運算能力的發(fā)展。因此，教師在課上應(yīng)該留出五分鐘的時間來歸納運算法則的要點，使學(xué)生能夠明確掌握并靈活運用運算法則，從而提高他們運算的速度，在運用所學(xué)運算法則的過程中還能發(fā)展學(xué)生的數(shù)學(xué)思維，提升其解題能力。

例如，在教學(xué)“乘法分配律”時，教師設(shè)計了以下幾個教學(xué)步驟，首先給學(xué)生呈現(xiàn)了以下兩個算式：①（6+4）×24;②6×24+4×24。然后讓學(xué)生說一說這兩個算式應(yīng)該先計算什么、再算什么？猜想自己的計算結(jié)果，通過分析學(xué)生得知第一個算式應(yīng)該先算括號中的，然后再與24相乘;第二個算式應(yīng)該先算兩個乘法，然后把兩個得數(shù)相加。接著，又給學(xué)生出示了兩組算式，讓他們比較算式的大小：①（2+3）×8 2×8+3×8;②（4+7）×6 4×6+7×6。學(xué)生對這兩組等式進(jìn)行觀察，然后有了有趣的發(fā)現(xiàn)，原來等式兩邊是相等的。于是，教師帶領(lǐng)學(xué)生共同歸納乘法分配律，讓學(xué)生結(jié)合實際練習(xí)來掌握這一運算法則，從而做到靈活的運用。

3. 靈活運用“三算”

三算是指口算、估算、筆算。其中口算是學(xué)生估算、筆算的基礎(chǔ)，也是運算能力培養(yǎng)中不容或缺的一部分。在三算教學(xué)中，教師必須給學(xué)生提供具體的計算情境，引領(lǐng)學(xué)生利用多種方法來審題、思考，在完成運算之后對結(jié)果進(jìn)行估算，以達(dá)到驗算的目的。如此一來，既有利于培養(yǎng)學(xué)生及時驗算的好習(xí)慣，也有利于使他們的運算能力得以提高。

例如，在口算訓(xùn)練中，教師可以融入一些小游戲，如給學(xué)生準(zhǔn)備一副撲克牌，將其打亂分別給學(xué)生發(fā)放幾張，讓學(xué)生和同桌比大小，如果A的牌大則要進(jìn)行加法運算，比如A的牌是10，B的牌是2，那么兩個人要同時進(jìn)行運算，快速說出結(jié)果;如果B的牌大，則要進(jìn)行減法運算，在此過程中可以拉近學(xué)生間的互動，還有利于讓學(xué)生在玩中學(xué)，提高他們的口算速度。再如，教師先引領(lǐng)學(xué)生回憶了“特殊組合”，比如4×25=100，在此基礎(chǔ)上設(shè)計了看似復(fù)雜只要掌握規(guī)律就能快速計算的口算練習(xí)：①125×8，②25×12。并采取了競賽的方式，比一比在短短的一分鐘之內(nèi)誰可以快速將口算結(jié)果說出來，以此來激活學(xué)生的好勝心。學(xué)生通過思考可以把第一道算式轉(zhuǎn)化為（100+25）×4×2，進(jìn)而得出結(jié)果1000;把第二道算式轉(zhuǎn)化為25×4×3，進(jìn)而算出結(jié)果300。最后對最先說出答案的學(xué)生進(jìn)行表揚，這樣一來，可以提高學(xué)生運算的效率，增強他們運算的準(zhǔn)確率。

（三）探究運算思路

1. 緊扣本質(zhì)聯(lián)系

在運算教學(xué)中，有許多運算方法之間都是有一定聯(lián)系的，比如“數(shù)的加減運算”中就包括整數(shù)、小數(shù)和分?jǐn)?shù)的加減法，其中運算的原理也是相通的。因此，在學(xué)習(xí)“分?jǐn)?shù)的加減運算”時，教師可以引導(dǎo)學(xué)生利用知識間的本質(zhì)聯(lián)系來進(jìn)行遷移學(xué)習(xí)，使他們聯(lián)系以往所學(xué)的整數(shù)、小數(shù)的加減方法進(jìn)一步得出分?jǐn)?shù)加減的方法。這個過程是一個從舊知遷移到新知的過程，既能喚醒學(xué)生對所學(xué)知識的回憶，也有利于使他們不斷積累新的認(rèn)識，從而提高他們自主建構(gòu)新知的能力。

例如，“兩位數(shù)加減兩位數(shù)”這部分內(nèi)容是學(xué)生學(xué)加減法筆算的起始課，也是他們學(xué)習(xí)進(jìn)位加法、退位減法的重要基礎(chǔ)，所以，教師在課上先給學(xué)生安排了一個復(fù)習(xí)環(huán)節(jié)，給學(xué)生出示了幾道口算練習(xí)題：

73+3=? 48-30=? 35+2=

89-7=? 63-50=

教師提問：這是兩位數(shù)加減一位數(shù)，我們應(yīng)該怎么計算？通過復(fù)習(xí)的形式來喚醒學(xué)生的已有知識，促進(jìn)其從舊知遷移到新知。此外，教師還提問：“兩位數(shù)減整十?dāng)?shù)怎么減？”以此來激發(fā)學(xué)生的思考，讓他們進(jìn)行筆算，最后得出十位和十位相加減，個位和個位相加減的算法。在此過程中，學(xué)生可以找到加減一位數(shù)和加減兩位數(shù)之間的關(guān)系，通過對比聯(lián)系來重新建構(gòu)新的知識，提高他們探究新知的能力。

2. 自主探究思路

對運算知識的習(xí)得，并不是由教師單方面地“告訴”，而是讓學(xué)生通過自己的主動探究逐步獲得的。因此，教師要擺脫以往一人主導(dǎo)、過于獨斷的角色，在課上給學(xué)生提供更多“參與”“體驗”“探究”“發(fā)展”的空間和機會，使他們成為運算學(xué)習(xí)的“主人”，讓學(xué)生在教師的恰當(dāng)引導(dǎo)下結(jié)合所學(xué)、通過自己的思維能力來解決問題，這樣才能促進(jìn)其主體性的發(fā)展，讓學(xué)生的運算能力真正得到提升，并發(fā)展他們的綜合素養(yǎng)。

例如，在教學(xué)“乘法計算”的過程中，教師通過適當(dāng)提問的方式來對學(xué)生加以引導(dǎo)，鼓勵他們自主探究。首先，教師板書：18×11 23×11的豎式，引導(dǎo)學(xué)生仔細(xì)觀察這兩道式子的計算過程，并思考以下幾個問題：

①積是怎么得來的？

②積與第一個因數(shù)的兩個數(shù)字之間有什么關(guān)系？

③你發(fā)現(xiàn)了什么規(guī)律？

在學(xué)生自主思考的過程中能夠打開他們的思維，使學(xué)生得出兩位數(shù)如何與11相乘。接著教師引導(dǎo)學(xué)生進(jìn)行鞏固練習(xí)，讓他們完成以下運算：13×11= 32×11= 57×11= 71×11=，比一比誰算得又對又快。在實際練習(xí)的過程中，學(xué)生主動發(fā)現(xiàn)問題：在57×11這個式子中，5+7=12，這時應(yīng)該怎么辦？在發(fā)現(xiàn)了學(xué)生的疑惑之后，教師沒有說出答案，而是放手讓學(xué)生自己討論解決，交流心得體會。最后，通過自主探究學(xué)生得出“滿十進(jìn)一”的結(jié)論。在整個過程中，教師始終鼓勵學(xué)生自己獨立思考，充分鍛煉了他們的主體思維，讓學(xué)生獲得主體性的發(fā)展。

（四）求得運算結(jié)果

1. 符合運算規(guī)則

在理解算理之后，教師可以根據(jù)一些實例來引導(dǎo)學(xué)生對方法進(jìn)行歸納，讓他們知道算法是否與運算規(guī)則相符，是否符合運算本身發(fā)展的需要，這樣在今后的運算中才能做到“有跡可循”。

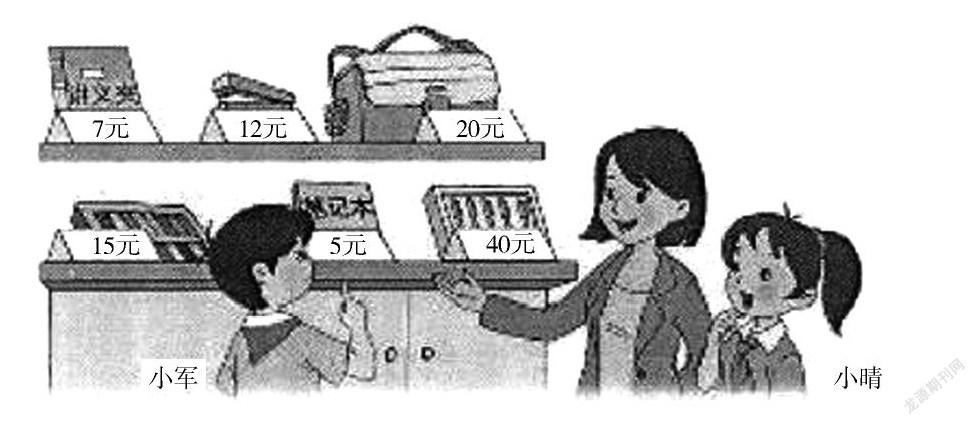
例如，在教學(xué)“混合運算”時，教師給學(xué)生出示了一道例題：小剛?cè)ド痰曩I文具，買了3本筆記本和1個書包，請你根據(jù)下圖幫他計算一下一共需要多少錢？

當(dāng)學(xué)生理解題意列出分步算式：5×3=15（元） 15+20=35（元）后，教師引導(dǎo)學(xué)生列出算式“5×3+20”，并提問：你認(rèn)為這個算式里要先算哪一步？你是怎樣想的？學(xué)生結(jié)合分步算式的計算步驟和題意，理解了運算規(guī)則：這個算式里，要先算3本筆記本的價錢，所以要先算乘法，再算加法。通過這樣的分析幫助學(xué)生突破了“在沒有括號的乘法和加法兩步混合運算中，要先算乘法”這個難點，使學(xué)生明白這樣的想法是運算本身發(fā)展的需要，有跡可循。

2. 靈活運算方法

培養(yǎng)學(xué)生的運算能力并不是簡單地讓學(xué)生掌握運算方法，而是讓他們可以在不同的情境中來選擇相應(yīng)的方法展開運算，從而掌握合理選擇、靈活運用的技能。因此，教師要給學(xué)生提供具體的練習(xí)，引導(dǎo)他們根據(jù)題目中的數(shù)據(jù)來選擇靈活的方法，這樣在運算的過程中思維才會更開闊，學(xué)生掌握的方法自然也會越來越豐富。

例如，在引導(dǎo)學(xué)生學(xué)習(xí)“十幾減9”時，教師引導(dǎo)學(xué)生運用多種感官，邊操作小棒邊思考結(jié)果。在與同伴的交流中，獲得一些直觀體驗：可以一個一個減去……先從盒子里的10個中拿走9個，盒子里剩下1個，再把這1個和外面的3個桃合起來;先拿掉盒子外面的3個，再拿掉盒子里面的6個，這樣一共減去9個桃，最后還有4個桃;還可以想有聯(lián)系的加法算式“9+4=13”來算出得數(shù)，叫作“想加算減”，這種方法更加方便快捷。隨著深入學(xué)習(xí)，學(xué)生對想加、算減的方法越來越熟練。在不斷地螺旋上升的學(xué)習(xí)過程匯總，學(xué)生逐步掌握了100以內(nèi)的加減法，也積累了一定的計算經(jīng)驗和方法：拆分、根據(jù)數(shù)據(jù)靈活選擇方法……學(xué)生在求出運算結(jié)果時思維會更開闊，計算的方法也更豐富。

四、 結(jié)語

綜上所述，教師要努力擺脫以往機械訓(xùn)練的模式，充分依據(jù)小學(xué)階段學(xué)生的實際情況、原有的生活經(jīng)驗以及計算水平來開展多種多樣的教學(xué)活動，要把數(shù)學(xué)運算貫穿教學(xué)的始終，盡可能地讓運算訓(xùn)練與學(xué)生的日常生活互相貼近，喚醒學(xué)生以往的生活經(jīng)驗，降低學(xué)生對數(shù)學(xué)運算的畏懼感，促使學(xué)生結(jié)合已有經(jīng)驗、通過自己的思考來求得運算結(jié)果，在此過程中發(fā)展學(xué)生的運算思維，強化學(xué)生的運算技能，最終促進(jìn)其運算素養(yǎng)的形成和提升，從而實現(xiàn)核心素養(yǎng)的培育。

參考文獻(xiàn)：

[1]彭國慶.核心素養(yǎng)背景下小學(xué)生運算能力的培養(yǎng)策略[J].小學(xué)教學(xué)參考，2021（26）：1-3，105.

[2]邱光月.核心素養(yǎng)視覺下小學(xué)生數(shù)學(xué)運算能力的培養(yǎng)方法[C]∥課程教學(xué)與管理研究論文集（三），2021：129-131.