基于改進動態窗口法的移動機器人避障研究*

常新新，胡 為，姬書得，岳玉梅

(沈陽航空航天大學 a.航空宇航學院； b.自動化學院，沈陽 110136)

0 引言

自主避障[1-3]是移動機器人領域研究的重點及熱點問題。DWA算法[4-5]根據機器人的動力學與運動學特性得到一系列速度的離散值，然后用這些速度模擬接下來一段時間內機器人的軌跡，并采用評價函數評價這些軌跡，選取得分最高的軌跡對應的速度作為下一階段的速度。DWA算法在每一階段需要評價的軌跡數目較多，增加了避障時間，而且在評價軌跡時，權重參數的選取不當容易導致機器人在密集障礙物區無法選擇最佳路徑的問題[6]。文獻[7]提出了一種改進的DWA算法，通過引入代價函數，使用線性回歸模型對避障路徑成本進行估計，選擇較為合理的避障路徑。文獻[8]針對DWA算法，提出一種新的篩選允許速度的方法，針對非直接碰撞軌跡，在其終點處以其速度方向做射線，將與障礙物不相交的軌跡對應的速度設為允許速度。該方法考慮了預軌跡終點速度的方向，避免了部分可用速度被舍棄，使得機器人能夠選擇較合理的速度快速通過障礙物密集區。

針對DWA避障算法存在的問題，本文提出一種較優方位角范圍約束，即在模擬出預軌跡后，依據計算準則計算出較優方位角范圍，然后選取出下一時刻在較優方位角范圍內的預軌跡，最后通過軌跡評價函數確定最優軌跡對應的速度。該方法在原算法的基礎上進一步優化了允許速度的空間，一定程度上減少了需要評價的軌跡數目，減弱了權重參數在原算法中選擇最優速度時的決定性作用，提高了避障規劃的效率。

1 DWA算法

1.1 DWA算法簡介

DWA算法是基于機器人運動學與動力學理論的一種局部避障[9]算法，它將對機器人的位置控制轉換為對機器人的速度控制。DWA算法可以概括為三步：一是根據機器人自身的限制以及環境制約將速度的采樣空間約束在一定范圍內；二是根據機器人運動學對采樣后的速度進行模擬得到預軌跡；三是設定評價函數對預軌跡進行評分以獲取最優軌跡對應的執行速度。

1.1.1 速度采樣空間[10-11]

根據機器人自身最大速度和最小速度限制，速度Vs(v,w)(v表示機器人的線速度，w表示機器人的角速度)滿足：

Vs={(v,ω)|vmin≤v≤vmax,ωmin≤ω≤ωmax}

(1)

考慮到機器人驅動力的約束，存在最大的加減速限制，進一步將速度空間進行約束，用Vd表示。假設機器人當前線速度為Vc，當前角速度為ωc，時間間隔為t，則下一時刻的可達速度Vd(v,w)滿足如下條件：

(2)

基于移動機器人的安全考慮，為了能夠在碰到障礙物前停下來，因此在最大減速條件下，速度滿足：

(3)

式中，dist(v,ω)為速度(v,ω)對應軌跡上離障礙物最近的距離。該碰撞條件是在機器人軌跡模擬出來之后，根據機器人與障礙物之間的距離，然后計算當前采樣的速度能否在碰到障礙物之前停下，如果能夠停下來，該速度就是允許的速度。

機器人最終的速度采樣空間為:

Vr=Vs∩Vd∩Va

(4)

1.1.2 速度采樣及軌跡生成

人為設定速度采樣的線速度分辨率以及角速度分辨率，得到所有速度組合。根據機器人運動學模型對采樣的速度進行模擬，得到一系列下一時刻的預軌跡。

1.1.3 軌跡評價

采樣的速度中，不止一組速度對應的軌跡是可行的，為了獲取最優的執行速度，采用評價函數對每條軌跡進行評價。評價函數定義為：

G(v,w)=σ(α·heading(v,w)+β·dist(v,w)+γ·velocity(v,w))

(5)

式中，使得G(v,w)值最大的速度為最優速度；函數項heading(v,w)中heading=π-φ(φ表示用來評價機器人在當前設定的采樣速度下，達到模擬軌跡末端機器人的航向與目標線的夾角)，如圖1所示。

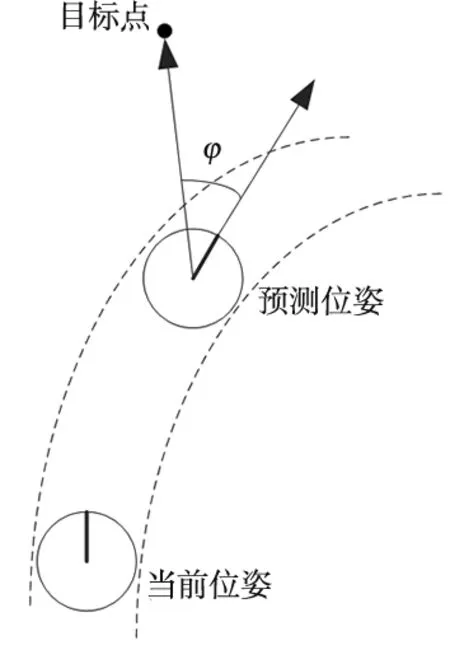
圖1 機器人方位角

函數項dist(v,w)用來評價機器人在當前軌跡上與最近的障礙物之間的距離，若這條軌跡上沒有障礙物，則設定一個常數；函數項velocity(v,w)評價當前軌跡對應的速度大小，速度越大的評分越高；α,β,γ為3個參數，代表每一個函數項的權值。

待評價項heading(v,w)、dist(v,w)和velocity(v,w)計算出來后，需要做歸一化處理，然后再相加，歸一化的準則是每一項除以每一項的總和。即：

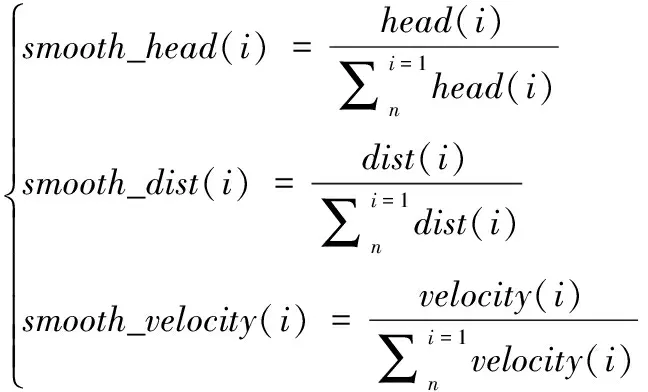
(6)

式中，i為待評價的當前軌跡點，n為采樣的所有軌跡點。

1.2 改進的DWA算法

本文提出一種改進的DWA算法，在模擬出下一時刻的預軌跡后首先根據計算準則確定機器人前進的較優方位角范圍，然后選取出較優方位角范圍以內的預軌跡，最后通過軌跡評價函數確定最優軌跡對應的速度。

當機器人前進方向上有多個障礙物時，根據機器人攜帶的單線激光雷達觀測到的障礙物的方位信息，計算可通行的較優方位角范圍。具體步驟如下：

(1)坐標系轉換

為方便計算，將激光雷達坐標系原點與機器人坐標系原點重合，建立機器人極坐標系以及全局坐標系，將機器人的方位角變換到全局直角坐標系下。如圖2所示，機器人在全局坐標系下的方位角為α，β為極坐標系與全局坐標系的變換角。

β=α-90°

(7)

已知機器人極坐標系下終點的方位角為φ，則在全局坐標系下的方位角為φ1，表示為：

φ1=φ-β

(8)

式(8)為機器人方位角由極坐標系轉換到全局坐標系下的轉換公式。

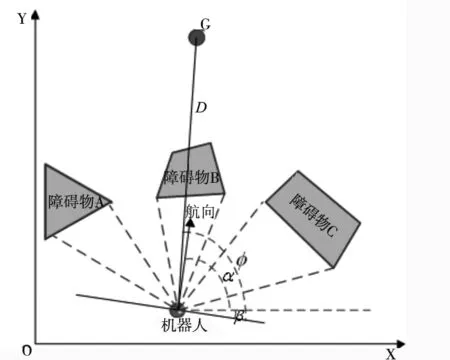
圖2 坐標轉換圖

(2)可通行區域判定

如圖3所示，在機器人極坐標系下，以θ2角度區域為例，如果相鄰障礙物間的距離c≥dr(dr為機器人的寬度)，則可判定該區域為可通行區域[12]，否則為不可通行區域。圖4中a和b分別為機器人到障礙物A與障礙物B的距離，由余弦定理可得，兩障礙物間的最近距離c為：

(9)

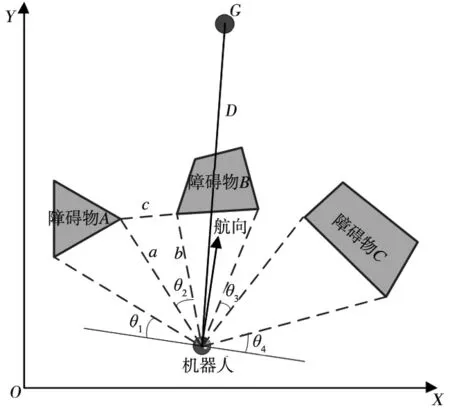
圖3 可通行區域判定

(3)較優方位角范圍確定

在機器人運行環境已知的情況下，當機器人距離目標較遠時，為避免機器人轉動太大角度，優先考慮與機器人航向較近的可通行區域，因此將機器人當前航向與可通行區域夾角較小的方位角范圍設為較優方位角范圍；反之，當機器人與目標點距離較近時，將目標線與可通行區域夾角較小的方位角范圍設為較優方位角范圍。

由于機器人在躲避障礙物過程中行走的路徑不規則，機器人與目標點的距離可能不會呈單調遞減趨勢，因此設定距離準則以描述機器人距離目標點的遠近。如圖4所示，在全局坐標系下，機器人初始y坐標為y0，以機器人和目標點在y方向的坐標差描述兩者距離的遠近。較優角度區域的計算準則為：

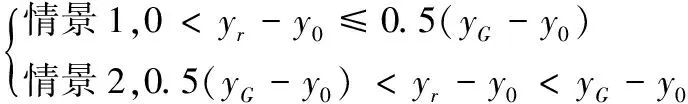
(10)

yG-y0表示目標點和機器人起始點在y方向的坐標差；yr-y0表示機器人某時刻y方向的坐標與起始點y坐標的差值。

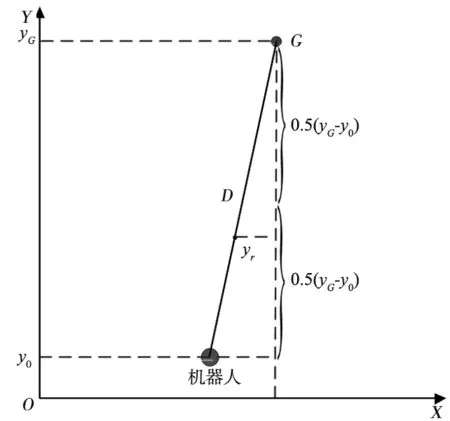
圖4 機器人與目標點的距離準則

較優方位角范圍確定方法如下：

情景1：當機器人與目標方向較遠時，計算機器人當前航向與可通行區域夾角較小的方位角范圍。如圖5所示，在極坐標系下，機器人共有4個可通行的候選方位區域：θ1,θ2,θ3,θ4，其中與機器人當前位置最接近的角度區域為θ2和θ3。θ2和θ3均為機器人下一時刻的可通行區域，通過比較θ2和θ3區域與目標線的角度差β1和β2，可知β1>β2。因此可將與航向較近的θ3區域設為機器人前進的較優方位區域。

θ3角度區域的起始為γ1，終止角度區域為γ2，轉換到全局直角坐標系下表示為：

(11)

即機器人下一時刻前進的較優方位角范圍為[γ1-β,γ2-β]。

圖5 機器人航向與可通行區域關系示意圖

假設機器人坐標系下，預測軌跡的終點的方位角為η，預測軌跡的終點和機器人當前位置的連線與較優角度區域邊界的夾角滿足：

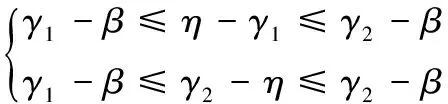
(12)

情景2：當機器人與目標點距離較近時，計算目標線與可通行區域夾角較小的方位角范圍。同理，由圖6可知，通過計算，θ2和θ3均為可通行的區域，通過比較θ2和θ3區域與機器人航向的角度差β3和β4，可知β3<β4。因此可將與目標點較近θ2區域設為機器人前進的較優方位區域。

θ2角度區域的起始為γ3，終止角度區域為γ4，轉換到全局直角坐標系下表示為：

(13)

即機器人下一時刻前進的較優方位角范圍為[γ3-β,γ4-β]。

圖6 目標線與可通行區域關系示意圖

此時預測軌跡的終點和機器人當前位置的連線與較優角度區域邊界的夾角滿足：

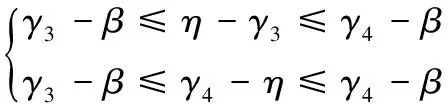
(14)

改進后的DWA算法步驟如下：

(1) 根據傳感器信息，得到機器人與障礙物的距離及方位，確定可通行區域；

(2) 根據機器人的動力學與運動學特性以及機器人當前速度和加速度，在速度采樣空間中對v與ω進行離散采樣，得到一系列速度(v，ω)；

(3) 根據機器人運動學特性對采樣的速度進行模擬，進而得到一系列預軌跡。根據以上準則及方法計算下一時刻機器人前進的較優方位角范圍，剔除較優方位角范圍以外的軌跡對應的速度；

(4) 采用評價函數對剩余的軌跡進行評價，首先將評價項按照式(6)的方法進行歸一化處理，然后根據式(5)求出評價得分最高的一組軌跡對應的速度(v，ω)作為下一時刻的執行速度。

(5) 執行最優速度，判斷是否到達目標點，若是，則結束運行；若否，則返回第一步，進入下一步循環。

2 改進的DWA算法仿真實驗

對原DWA算法以及改進的DWA算法進行仿真，仿真環境為MATLAB 2019b，并對結果進行分析。DWA算法涉及了機器人自身的多個參數以及算法參數，選取的參數如表1和表2所示。

表1 機器人自身參數

表2 原DWA算法參數

為了充分證明改進的DWA算法的可行性以及避免算法適用環境的偶然性，本文設計了兩種機器人運行環境，并進行仿真實驗，如圖7、圖8所示，驗證在不同環境下，改進的DWA算法在局部避障中的可行性及優勢。

在仿真時，將機器人當作質點處理，但是在實際運行中，機器人是有一定體積的，因此采用障礙膨脹處理的方法將機器人的尺寸考慮到障礙物上，仿真中采取的障礙物膨脹半徑為0.4 m。兩種運行環境中機器人起點分別為(0,0)和(12,0)，目標點分別為(12,14)和(0,14)，為便于區分對比，將原DWA算法實驗的路徑軌跡設置為藍色，將改進的DWA算法實驗的路徑軌跡設置為綠色。由原DWA算法仿真的軌跡圖可知，機器人在運行過程中容易陷入局部最優，而且在密集障礙物區選擇的路徑不是最佳路徑，規劃的避障路徑相對較遠，若在實際運行中可能會增加機器人遇到動態障礙物的概率，從而降低運行的效率。由改進后的DWA算法仿真結果可以觀察出，兩種不同的運行環境下，機器人在密集障礙物區能夠選擇較優方位角區域的速度運行，機器人付出的的代價較小，而且運行后的軌跡較為平滑。

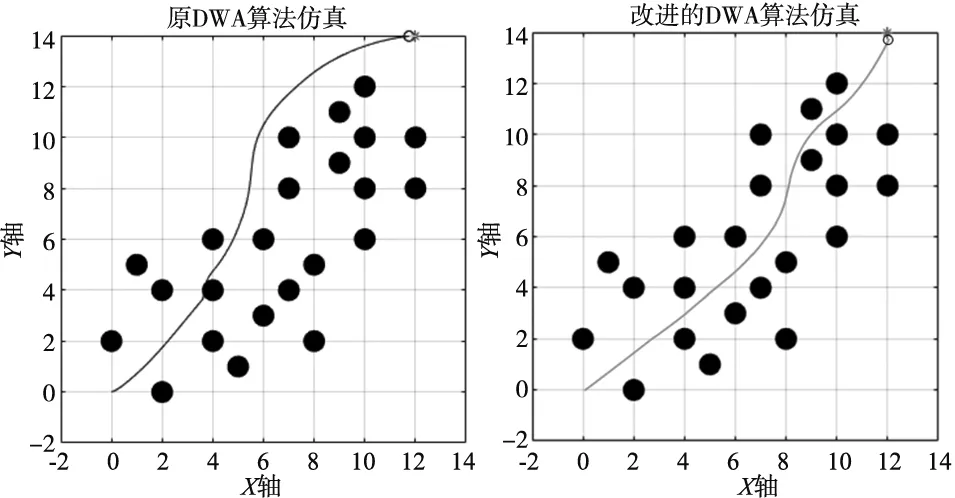
(a) 原DWA算法仿真軌跡圖 (b) 改進的DWA算法仿真軌跡圖圖7 運行環境1

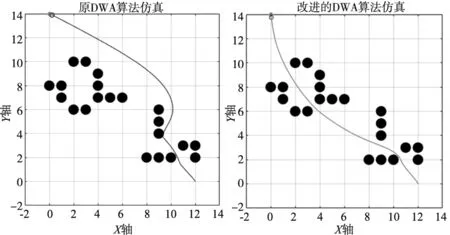
(a) 原DWA算法仿真軌跡圖 (b) 改進的DWA算法仿真軌跡圖圖8 運行環境2

對算法改進前后的迭代次數與運行時間進行定量分析，如表3所示。由于運行環境設置的復雜性以及時間分辨率較低等因素，導致避障中算法迭代的次數較多、運行時間比較長。但在參數設置相同的情況下，改進后的DWA算法迭代次數相比原DWA算法要少，減少了需要評價的軌跡數目，而且運行所用的時間少，在避障效率上有所提高。

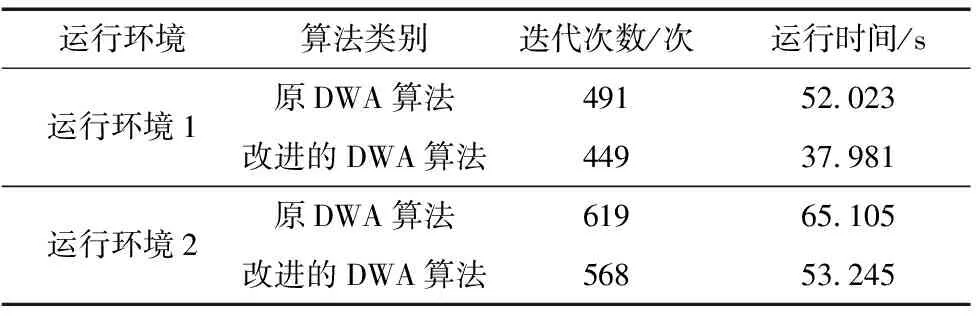
表3 改進前后迭代次數與運行時間對比

3 結論

本文通過改進DWA算法對移動機器人避障效果進行優化，針對DWA算法提出了一種較優方位角范圍約束及其計算準則優化允許速度空間。改進后的DWA算法在一定程度上減少了需要評價的軌跡數目，減弱了原算法中權重參數對最優軌跡的決定性作用。仿真結果表明：在密集障礙物區，采用改進的DWA算法，機器人能夠以最佳路徑選擇較優的區域通過，避障效率得到提高。本文只是將改進的DWA算法在仿真環境下進行了避障規劃實驗，下一步將進行實物實驗驗證改進算法的有效性。