基于AdvantEdge切削工藝參數及刀具幾何參數對切削力影響研究

胡 波，趙先鋒，史紅艷，胡小龍，湯朋飛

(貴州大學機械工程學院，貴陽 550025)

0 引言

Ti6Al4V合金具有質量輕、強度高、耐高溫等性能，廣泛應用于飛機發動機壓氣機部件、火箭、導彈和高速飛機的結構件等領域[1-2]，但由于其較低的導熱性、較高的化學活性以及彈性模量較小等缺點，故而在進行切削時難免會出現切削溫度高、刀具磨損嚴重等問題，以至于企業在加工過程中產生的成本較高[3]。

切削加工過程中，切削工藝參數和刀具幾何參數以及環境因素等都對切削力的改變有直接或間接的關系[4-7]。關于切削力的研究最開始是由Kienzle O[8]使用經驗方法得出切削過程中產生的切削力，即將橫截面面積和特定能量系數乘積來表示切削力。關于切削工藝參數和刀具幾何參數時怎么影響切削力這個問題國內外學者一直在研究，而絕大多數學者是在研究高速切削下的影響，這其中對高速銑削的研究居多。關于硬質合金材料的刨刀，由于其切削時獨特的切削方式限制了切削速度，并在回程時不切削，故而切削效率不是很高，但刨削所需的機床、刀具結構簡單，制造安裝方便，調整容易，通用性強。因此在單件、小批生產中特別是加工狹長平面時被廣泛應用。

本文就基于AdvantEdge對正交刨削進行有限元分析，通過29組在不同加工工藝參數下的仿真結果，采用單因素變量對仿真的切削工藝參數和刀具幾何參數進行分析，總結出在低速切削下進給量、切削速度、切削深度、工件初始溫度、前角、后角、刀刃鈍圓半徑對切削力的影響。同時找出影響切削力最主要的4個因素即切削深度、進給量、前角和鈍圓半徑，建立進給抗力指數公式、主切削力指數公式和切削合力指數公式，利用回歸分析和最小二乘法解得各參數，最后將計算結果與仿真結果對比效果良好，具有一定的理論參考價值。

1 正交刨削切削模型的建立

1.1 材料本構模型

本文以AdvantEdge[9-10]進行仿真，本構模型為應用廣泛的Johnson-Cook：

(1)

式中，A是初始屈服應力，單位是MPa；B是應變硬化常數，單位是MPa；C是特性系數；m是熱軟化系數；n是切削硬化指數，見表1。

表1 Ti6Al4V的JC模型參數[11]

1.2 材料的力學性能

刀具材料為硬質合金刀具，切削材料為Ti6Al4V合金，兩者主要的物理性能如表2所示。

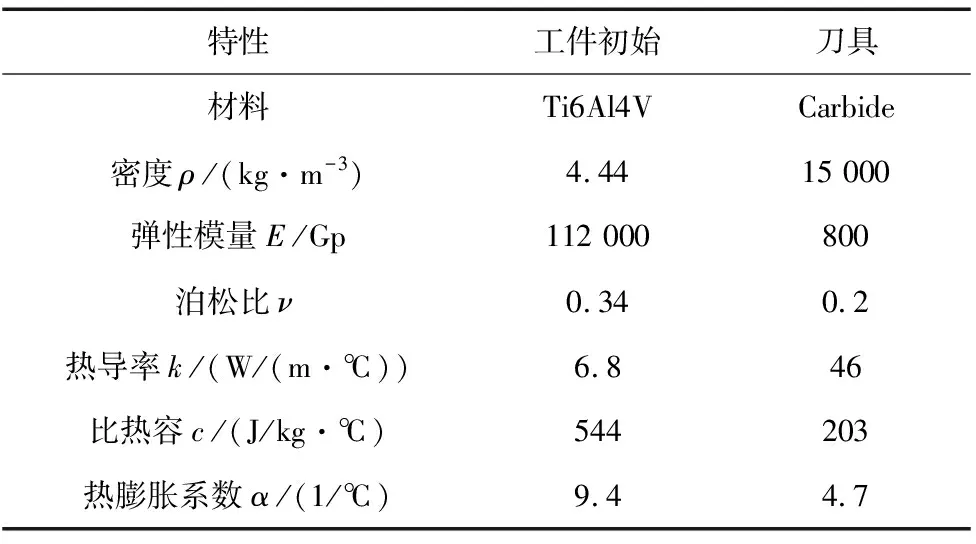
表2 工件和刀具材料的物理性能

1.3 有限元仿真模型

本文目的時為了驗證正交刨削[12]時，切削工藝參數及刀具幾何參數對切削力的影響，故而為了方便對比，將對29組參數進行仿真，通過查閱鈦鋁合金Ti6Al4V的機械強度與鋼相差不多，故而吧切削過程中的硬質合金刀對鈦合金看作鋼對鋼的過程，設置摩擦系數為f=0.2，網格為0.007。表3為仿真時會涉及到的切削工藝參數和刀具幾何參數。

表3 切削工藝參數和刀具幾何參數

圖1為仿真過程，仿真結果含進給抗力和主切削力，切削合力通過下式計算：

(2)

式中，Fx為進給抗力，Fy為主切削力。

圖1 AdvantEdge模擬切削

2 仿真結果分析

從仿真結果圖(見圖2)我們可以知道，整個的切削過程主要劃分為兩個過程即初始切削階段和穩定切削階段。初始切削階段為刀具剛開始接觸工件初始，由于電機的轉動而使得刨刀高速旋轉工件初始逐漸形成切屑，主切削力和進給抗力同時增長，但主切削力增加較快；穩定切削階段，電機旋轉穩定，刀具渡過磨合使得主切削力和進給抗力均趨于穩定，但隨著各種參數的不斷改變，我們可以通過將AdvantEdge仿真得到的結果依次進行控制變量分析。

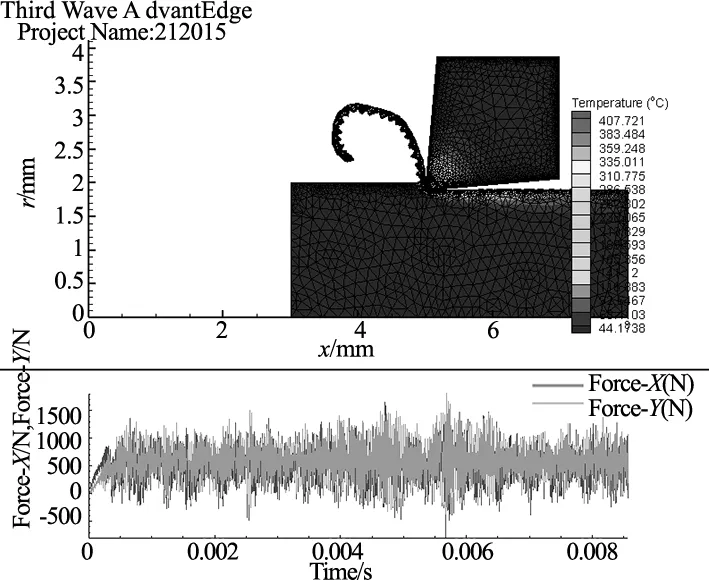
圖2 仿真結果

2.1 進給量對切削力的影響

圖3為不同進給量(0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm)下X、Y和切削合力的變化曲線圖，其他設置參數分別為切削深度5 mm、切削速度15 m/min、前角10°、后角5°、摩擦系數u=0.2以及鈍圓半徑為0.1 mm，表4為仿真結果。從圖中可以看出：隨著進給量的增加，進給抗力、主切削力和切削合力都在增加，非正比變化。主要原因為：低速切削情況下，隨著進給量的增加會出現積屑瘤，同時隨著相同圈數所切削的長度相對變長而使得進給時的阻力變大，故而直接影響進給抗力的增加，間接影響主切削力和切削合力。

表4 不同進給量下仿真結果

圖3 進給量對切削力的影響

2.2 切削速度對切削力的影響

圖4是切削速度分別為15 m/min、21 m/min、30 m/min、40 m/min進行仿真所得結果，其余設置參數分別為：切削深度5 mm、進給量0.1 mm/r、前角10°、后角5°、摩擦系數u=0.2以及鈍圓半徑為0.02 mm，表5為仿真結果。通過圖4可知總趨勢為各切削力隨切削速度的增加而增加。形成的主要原因為：隨著切削速度的增加，積屑瘤也在漸漸增加，直接影響為各切削力的增加。

表5 不同切削深度下仿真結果

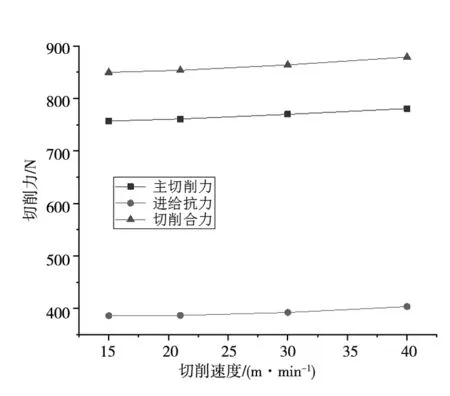
圖4 切削速度對切削力的影響

2.3 切削深度對切削力的影響

圖5是切削深度分別為2 mm、3 mm、4 mm、5 mm時切削深度與切削力的變化曲線圖，其他參數設置為：切削速度15 m/min、進給量0.1 mm/r、前角10°、后角5°、摩擦系數u=0.2以及鈍圓半徑為0.02 mm，表6為仿真結果。由曲線圖可知：切削力隨切削深度的增加而增加且呈線性增長，其次切削深度對各個方向切削力的影響是比較大的，特別是對主切削力的影響。主要原因為：切削深度的增加切削厚度不變，而切削寬度增加，切削刃上的切削負荷也增加，最終表現為對主切削力的影響大而進給抗力相對較小。

表6 不同切削深度下仿真結果

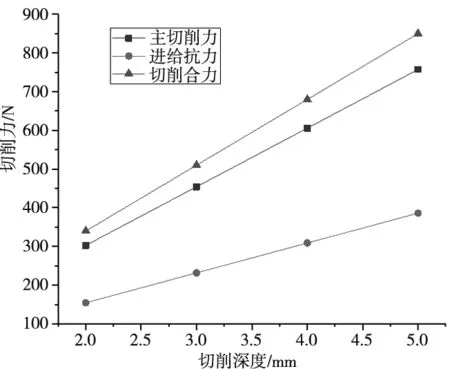
圖5 切削深度對切削力的影響

2.4 工件初始溫度對切削力的影響

圖6 是工件初始溫度設置為20 ℃、40 ℃、60 ℃、80 ℃時的切削力變化曲線圖，其余參數設置為切削速度15 m/min、進給量0.1 mm/r、切削深度5 mm、前角10°、后角5°、摩擦系數u=0.2以及鈍圓半徑為0.02 mm，表7為不同工件初始溫度下的仿真結果。由圖可知：隨著工件初始溫度的增加，切削力是減小的，主要原因是隨著工件初始溫度增加會使得工件材料“軟化”，即材料的硬度和剛度會減小，最終表現為各個切削力的減小。

表7 不同工件初始溫度下仿真結果

圖6 工件初始溫度對切削力的影響

2.5 前角對切削力的影響

圖7是前角設置為5°、10°、15°、20°時的切削力變化曲線圖，其余參數設置為切削速度15 m/min、進給量0.1 mm/r、切削深度5 mm、后角5°、摩擦系數u=0.2以及鈍圓半徑為0.02 mm，表8為不同前角下的仿真結果。由圖可知各方向切削力隨前角的增大而逐漸減小，且越到后面越趨于平穩，主要原因是隨著前角的增大，使得剪切角增大，導致變形系數減小，即最終表現為切削力的減小。

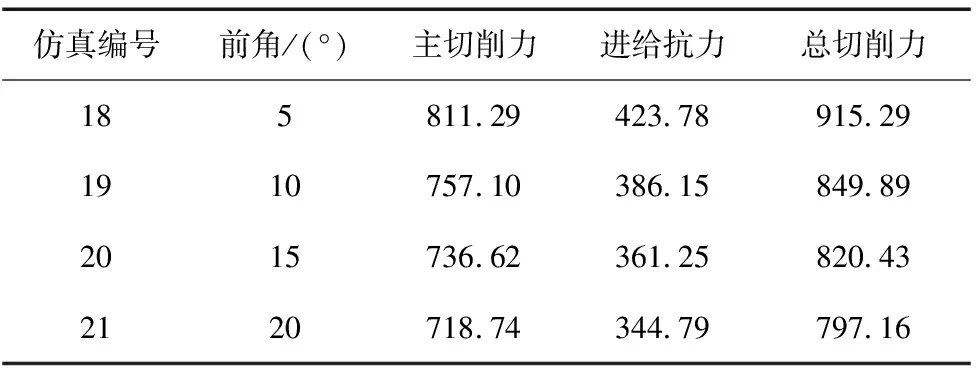
表8 不同前角下仿真結果

圖7 前角對切削力的影響

2.6 后角對切削力的影響

圖8 是后角設置為5°、10°、15°、20°時的切削力變化曲線圖，其余參數設置為切削速度15 m/min、進給量0.1 mm/r、切削深度5 mm、前角10°、摩擦系數u=0.2以及鈍圓半徑為0.02 mm，表9為不同后角下的仿真結果。由圖可知后角對進給抗力幾乎沒有影響，對主切削力和切削合力有細微影響。主要原因是隨著后角的增大，會使得刀刃的鋒利度增加，但同時也會使得切削刃強度降低，由于是低速切削故而切削的鋒利度對切削力的影響并不明顯，反而在低速情況下后角的增加會使得切削力有細微的減小。

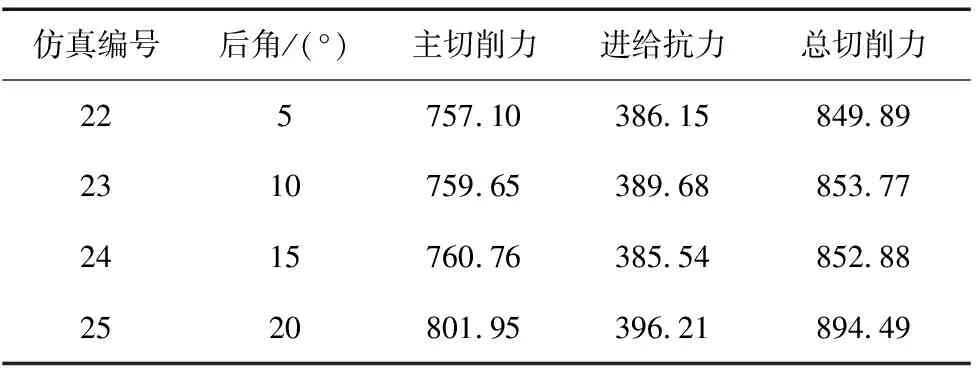
表9 不同后角下仿真結果

圖8 后角對切削力的影響

2.7 鈍圓半徑對切削力的影響

圖9是正交切削時鈍圓半徑設置為0.002 mm、0.004 mm、0.008 mm、0.1 mm時的切削力變化曲線圖，其余參數設置為切削速度15 m/min、進給量0.1 mm/r、切削深度5 mm、前角10°、后角5°以及摩擦系數u=0.2，表10為不同鈍圓半徑下的仿真結果。由變化曲線圖可知，鈍圓半徑對主切削力的影響相對于進給抗力的影響較小，總的趨勢為隨著鈍圓半徑的增加而增加。主要原因為：刀尖鈍圓半徑的增加會使得切削曲線部分的長度和切削寬度增大，但切削厚度會減薄，導致各點的主偏角減小，最終表現為鈍圓半徑的增加使得主切削力和進給抗力增加，而進給抗力增加明顯。

表10 不同鈍圓半徑下仿真結果

圖9 鈍圓半徑對切削力的影響

3 切削力預測

通過分析切削工藝參數和刀具幾何參數對切削力的影響，得出進給量、切削深度、前角以及鈍圓半徑對切削力的影響最明顯，故而建立以切削深度、進給量、前角和鈍圓半徑為變量，分別以主切削力、進給抗力和切削合力為因變量的指數模型公式，即：

Fx=C1apa1fb1γc1rd1

(3)

Fy=C2apa2fb2γc2rd2

(4)

F=C3apa3fb3γc3rd3

(5)

式中，Fx、Fy和F分別表示進給抗力、主切削力和切削合力；ap、f、γ和r分別表示切削深度、進給量、前角和鈍圓半徑；ax、bx、cx、dx分別表示切削深度、進給量、前角和鈍圓半徑的指數，x=1、2、3；C1、C2、C3為常數。

通過SPSS軟件對仿真編號1～5、11～13、18～21、26～29共16組數據進行回歸分析，得到各變量的指數，并通過最小二乘法計算出C1、C2、C3后得到指數模型公式分別為：

Fx=5052.35×ap0.165×f0.421×γ-0.043r0.503

(6)

Fy=9657.05×ap0.151×f0.761×γ-0.019×r0.262

(7)

F=13296.15×ap0.157×f0.677×γ-0.024×r0.384

(8)

為了說明3個公式的顯著性，對3個建立的模型進行方差分析，分析結果見表11。

表11 方差分析

如上表所示，3個方差分析中回歸平方和的自由度均為4，殘差平方和的自由度均為16，通過查檢驗表得F0.01(4，16)=4.77，F0.05(4，16)=3.01，從表11可以看出幾個模型F值遠大于F0.01(4，16)，概率值p=0.00<α<0.01，故回歸模型擬合度很高，線性回歸效果為高度顯著。

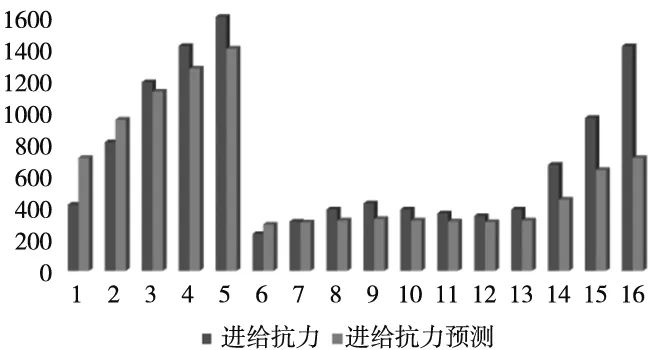
(a)進給抗力預測對比

(b) 主切削力預測對比

(c)切削合力預測對比 圖10 指數公式計算計算結果與仿真對比

通過計算結果和仿真結果進行對比可以發現，其相差很小，僅有極個別點會存在大誤差，故而在排除一些非人為影響因素后，該模型是具有一定可借鑒性的。

4 結論

本文基于AdvantEdge軟件進行有限元分析，通過29組在不同切削工藝參數和不同刀具幾何參數的條件下對工件材料Ti6Al4V合金進行切削仿真， 探究了各變量對切削力的影響，故而可得結論為：

(1)切削工藝參數：各方向切削力隨進給量的增加而增加，但非線性；各切削力隨切削速度的增加而增加；切削力隨切削深度的增加而增加且呈線性增長，其次切削深度對各個方向切削力的影響是比較大的，特別是對主切削力的影響；隨著工件初始溫度的增加，切削力減小。

(2)刀具幾何參數：各方向切削力隨前角的增大而逐漸減小，且越到后面越趨于平穩；在低速情況下后角對進給抗力幾乎沒有影響，對主切削力和切削合力有細微影響，主要表現為后角增加會使得切削力有細微的減小；鈍圓半徑對主切削力的影響相對于進給抗力的影響較小，但總的趨勢為隨著鈍圓半徑的增加而增加。

(3)通過SPSS對數據的回歸分析，擬合出進給抗力指數公式、主切削力指數公式和切削合力經驗公式。

基于上述結論得出在低速正交刨削時，和高速切削時會有些許一樣的結論，故而在加工時我們應該針對低速、中速和高速切削設定變化范圍，分段式的建立不同速度下的結論。