BAS-LSA混合算法在裝配序列規劃的應用*

任 云，劉 丹

(貴州大學現代制造技術教育部重點實驗室，貴陽 550025)

0 引言

裝配是生產制造的重要環節，直接關系到產品質量、性能、壽命和可維護性，裝配序列規劃是裝配工藝規劃的重要部分，序列的優劣直接影響裝配質量[1]。裝配序列規劃研究可以優化裝配順序，使企業獲得生產成本更低、裝配效率更高、質量更佳的裝配方案。裝配序列規劃是一個典型的非確定性多項式(Non deterministic polynomial,NP)組合優化問題[2]，產品的裝配序列數量與產品的零部件數量呈指數增長關系，越復雜的產品越容易遇到裝配序列組合爆炸問題[3]，這給裝配規劃問題帶來了很大的挑戰。

為了更好解決這一問題，研究者將各類智能優化算法如遺傳算法[4]、蟻群算法[5]、模擬退火算法[6]、神經網絡算法[7]等應用到裝配序列規劃中，這些算法在一定程度上克服以往方法中存在的組合爆炸問題及裝配的局限問題。遺傳算法是目前在裝配序列規劃中應用最為廣泛的算法，但遺傳算法要求初始種群為可行序列，且全局收斂速度慢和存在大量重疊迭代的問題；蟻群算法在裝配序列規劃問題中也有廣泛的應用，但它運算效率較低，且開始階段信息素積累較慢，容易陷入局部最優[8]，針對上述問題，論文根據裝配序列規劃問題的特點，提出將閃電搜索算法和天牛須算法運用于裝配序列規劃之中。

閃電搜索算法(Lightning Search Algorithm,LSA)是Shareef H等受自然天氣中閃電現象的啟發提出的一種優化算法[9]，Dorigo M等將其應用于函數優化和TSP(Traveling Salesman Problem)問題[10]，并取得了良好的優化效果, Islam M M等提出了一種基于二進制編碼的閃電搜索算法[11]，證明了該算法在搜索精度和收斂性方面性能表現良好。

由于LSA算法模擬閃電的快速傳播特性，因此收斂速度較快。但LSA算法本身存在求解精度不高、易陷于局部最優等缺點。

天牛須搜索算法(Bettle Antennate Search Algorithm,BAS)在2017年由Jiang X等根據天牛個體用左右觸須感受食物氣味的方向逐漸接近食物這一特點提出的[12]。研究表明BAS算法在搜索速率與搜索精度上均可達到理想的結果。BAS算法局部搜索能力很強，但全局搜索能力不足。因此，本文結合天牛須搜索算法和閃電搜索算法的優點，提出將天牛須搜索算法和閃電搜索算法混合的裝配序列規劃優化方法,以此來解決閃電搜索算法容易陷入局部最優的問題，提高跳出局部最優的能力和搜索精度。

1 BAS和LSA的基本原理

1.1 LSA算法的基本原理

閃電搜索算法(LSA)是對閃電這種自然現象的觀察而得到的新新算法，當閃電形成時，空氣中的“放電粒子”與空氣碰撞之后會產生一條電離路徑或通道，并形成一條梯級先導。LSA算法利用空間放電體、和引導放電體等概念建立分布函數模型來求解待解決的問題[13]，空間放電體試圖成為最優梯級先導，引導放電體代表種群中的最優個體[14]。

(1)在一個種群規模為N，初始種群的生成服從均勻分布，創建初始隨機種群，其概率密度函數f(xc)可以表示為：

(1)

式中，xc是一個候選解，a和b分別是“放電粒子”范圍的最小值和最大值。

(2)引導放電體表示為HL，由正態概率密度函數f(xk)來生成位置：

(2)

式中，μ為形狀參數，引導放電體HL在下一次迭代的位置為：

(3)

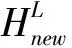
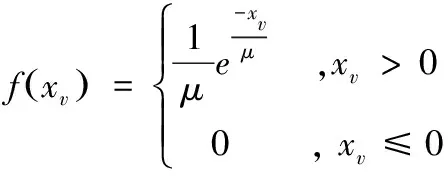
(4)

形狀參數μ會影響CS和HL之間的距離，CS在下一次迭代的位置為：

(5)

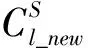
(4)分叉是放電體的另一特性，在LSA算法中分叉有兩種方式，首先分叉會形成兩個互相對稱的通道：

rl=e+g-rl

(6)

其中，e和g表示邊界，rl和rl分別表示原來的通道和分叉產生的對稱通道。為了保證種群大小不變，兩通道只保留一個。

1.2 BAS算法的基本原理

天牛須搜索算法(BAS)是一種新的啟發式算法，它的特點是僅有一個天牛個體，所以運算速度很快，計算量低。

BAS算法的基本原理為：天牛個體在尋找食物的過程中通過左右觸須來感受食物的強度，因為兩須的位置不一樣，所以兩須所探測的強度也不一樣，天牛最終朝強度更大的觸須所指的方向前進一步，不斷重復上述流程，直到找到食物的具體位置。其中食物氣味相當于尋優函數，食物的具體位置相當于尋優函數的最優解。根據天牛的覓食過程抽象出的BAS算法遵循如下原則[15]：①天牛在物理世界尋找食物的過程可以到虛擬天牛在任意維空間求解函數最優值的情形；②天牛左右兩觸須對稱；③天牛每次向前移動的距離與兩須之間的距離成比例；④天牛每次前進后身體的方向不確定[16]。

根據以上原則，BAS 算法的數學表達如下：

(1)假設隨機產生的天牛方向為d，質心位置為x，右邊觸須位置為xr，左須為xl，兩須之間的距離為m，mt表示天牛在t時刻的兩須之間的距離，根據天牛的方向可以計算出左須和右須的位置：

xr=xt+dtb

(7)

xl=xt-dtb

(8)

(2)計算適應度值f(xl)和f(xr)的大小，比較兩者的大小，再決定天牛下一步的走向：

xt=xt-1+δtbsign(f(xr)-f(xl))

(9)

其中，xt為t時天牛的位置，sign為符號函數；δ為搜索步長，其大小是一個隨時間t逐漸衰減的函數值。t時刻的m與δ可表示為：

dt=etad*dt-1+0.01

(10)

δt=etaδ*δt-1

(11)

其中，eta_m和eta_δ分別為兩須之間的距離和步長的遞減系數，通常小于1。

(3)判斷求解結果是否達到理想的精度或迭代次數超過最大迭代次數，滿足一個條件就完成迭代，否則重復式(7)～式(10)的步驟。

2 裝配關系模型的構建

由于機械產品的裝配具有多種裝配方案，零件裝配序列有多種選擇，這增加了產品的復雜性，影響裝配時間、裝配成本以及裝配質量的因素有很多種，其中零件的幾何可行性、裝配方向、裝配工具的改變次數、零件之間的穩定性是主要影響因素，所以本文將以上4個因素作為評價指標。

2.1 幾何可行性

在裝配體上裝配零件Pi時，須考慮當前零件的裝配可行性，即Pi從無窮遠處沿方向v裝配時，前i-1個零件對Pi是否干涉。須首先構建6個方向的干涉矩陣[17]，如式子(12)所示，其中Pij表示零件j在裝配時零件i對零件j的干涉，有干涉Pij=1，無干涉Pij=0。并根據式(13)、式(14)判斷零件的裝配可行性。

(12)

(13)

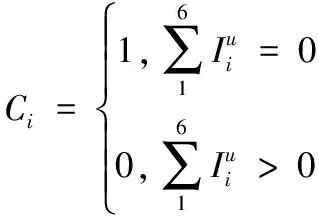
(14)

式中，n為裝配序列零件的個數，u為±X，±Y，±Z的一個方向，Ci=0表示零件pi裝配時會發生干涉，Ci=1中表示在某一方向上裝配是可行的。

2.2 連貫性

連貫性是指零件裝配過程中，相鄰零件Pi與Pi-1裝配方向是否相同。對于比較復雜的裝配體，裝配方向的改變會增加裝配難度，加大了對裝配工具的要求，同時還會明顯增加裝配時間和成本。由式(15)判斷零件pi與pi-1的裝配方向是否相同。

(15)

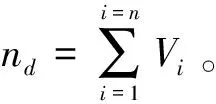
2.3 一致性

一致性是指裝配相鄰兩個零件時使用相同的裝配工具，如裝配零件的前后裝配工具不相同，中途還需更換裝配工具，這也增加了裝配的步驟，應盡量減少裝配過程工具的裝換次數，由式(16)判斷裝配工具的裝配次數。

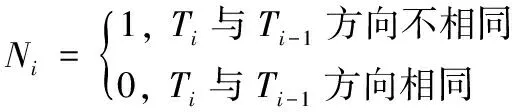
(16)

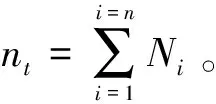
2.4 穩定性

穩定性是指裝配零件pi時，前一個零件pi-1對pi是否有支撐作用，如沒有支撐作用，則還需額外的支撐工具支撐pi的裝配，這就給裝配過程帶來額外的工作量，因此零件裝配過程需要考慮零件pi-1對pi的支撐作用，提高裝配效率，由式(17)評價裝配序列的穩定性。

(17)

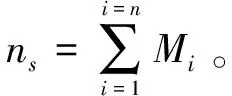
2.5 適應度函數

適應度函數通過從幾何可行性、連貫性、一致性、穩定性4個方面來評價序列。適應度函數如式(18)所示：

F(n)=w1*ng+w2*nd+w3*nt+w4*ns

(18)

其中，n為種群中第n個序列，ng為一條序列干涉次數之和，nd為裝配方向的改變次數，nt為裝配工具的改變次數，ns為無支撐作用的次數；w1、w2、w3、w4為權重系數；其中一條可行裝配序列的干涉次數應該為0，即ng=0，F越小表明這條序列越優。

3 LAS-BAS混合算法改進及步驟

LSA算法有求解精度低、容易陷入局部最優的缺點。BAS算法在全局的搜索能力較弱，且個體具有單一性，但局部搜索能力很強的特點，考慮將每一代經LSA求解的種群中不滿足幾何可行性的個體作為一個天牛須粒子以天牛須算法進行優化，提高LSA跳出局部最優的能力和搜索精度。

步驟1：設置算法的初始參數：最大迭代次數Nmax、種群規模N、梯級先導尖端能量El和最大通道時間T。

步驟2：生成隨機初始種群，計算放電體能量Ep和目標函數值大小。

步驟3：開始循環，更新梯級先導尖端能量El，找到最差、最優梯級先導。

步驟4：通道時間每次加一，如達到最大通道時間T，則淘汰適應度值最差的通道并重置通道時間。

步驟5：更新放電體方向和能量Ep，并計算引導放電體和空間放電體適應度值。

步驟6：計算放電體能量Ep，如果Ep>El，那么進入步驟6.1，否則進入步驟6.2；

步驟6.2：放電體的位置保持不變。

步驟7:計算種群中個體的幾何可行性，對于不滿足幾何可行性的個體，用天牛須搜索算法進行優化，并計算經優化后的個體適應度值，如果更優則替代當前個體，否則個體不變。

步驟8：如果迭代次數達到最大迭代次數，即結束迭代，進入步驟9，否則轉到步驟3，繼續增加迭代次數和通道時間，繼續迭代；

步驟9：得到最優先導，輸出最優解x。

根據上述步驟，LSA的基本流程如圖1所示。

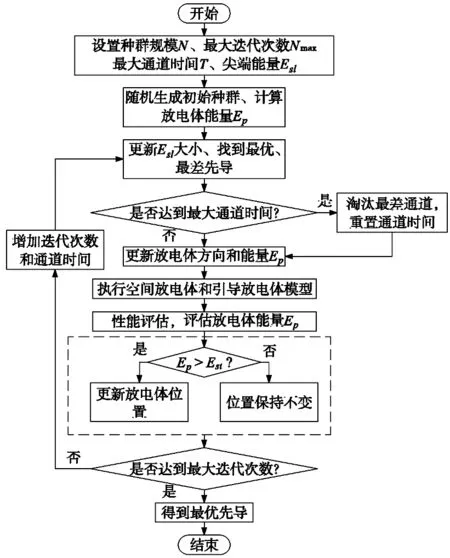
圖1 LSA-BAS算法流程圖

4 實例驗證及分析

如圖2所示，本文以蒸汽發動機引擎為例來進行算法驗證。該裝配體共包含18個零件。算法在MATLAB平臺上編寫，選擇的最大迭代次數Nmax為200，種群規模N為20。為了考察閃電搜索算法—天牛須搜索算法(LSA-BAS)的優化性能，將其與差分進化算法(DE)、粒子群算法(PSO)、閃電搜索算法(LSA)相比較，比較參數為最優適應度值、最優值迭代次數、跳出局部最優的能力等方面。

本文定義一個參數Q來描述各算法逃逸出局部最優的能力，Q的數值越小表明算法的逃脫局部最優的能力越強，其中L為最大迭代次數，ΔL表示找到最優適應度值前的所有局部最優區間，max(ΔL)表示其中所有局部區間的最大區間值，如式(19)所示：

(19)

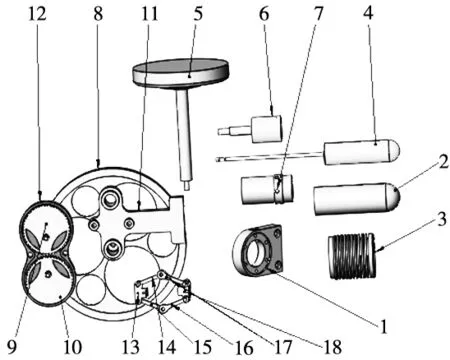
圖2 蒸汽發動機引擎裝配爆炸圖

表1為4種算法求出的最優序列，表2對4種算法求出的裝配序列幾個關鍵評價指標：干涉次數、無支持作用次數、裝配方向改變次數、裝配工具的改變次數進行比較。如表2所示，各算法干涉次數皆為0，這表明所有序列都是可行裝配序列，其中LSA-BAS混合算法的支撐方向、裝配方向、裝配工具的次數改變之和為30，是4種算法中最小的，其中差分進化算法(DE)為35，粒子群算法(PSO)為32，閃電搜索算法(LSA)為32；LSA-BAS支撐方向的改變次數為9，是4個算法中最小的，工具的改變次數為11，同樣也是最小的。

表1 算法最優序列表

表2 裝配序列及相關數值對比

表3對4種算法的性能進行了對比。如表所示，混合算法的最優適應度值為3.35，比其它3種算法的適應度值都小，找到最優值的迭代次數為109，也比其它3種算法的迭代次數小，這表明混合算法的收斂速度及搜索精度強于其它3種算法。

表4中L為最大迭代次數，圖3為算法收斂曲線，從中可以得到局部最優最大區間。從表4算法局部最優對比可看出，在找到最優值迭代次數之前，混合算法陷入局部最優的最大代數為38代，Q值為0.19，遠小于其它3個算法的Q值，這表明LSA-BAS混合算法逃逸處局部最優的能力遠大于其它3種算法，并且最終除LSA-BAS混合算法外其它算法未能跳出局部最優，綜上所述表明混合算法在求解過程中，在全局搜索能力、搜索精度及跳出局部最優方面有明顯優勢。

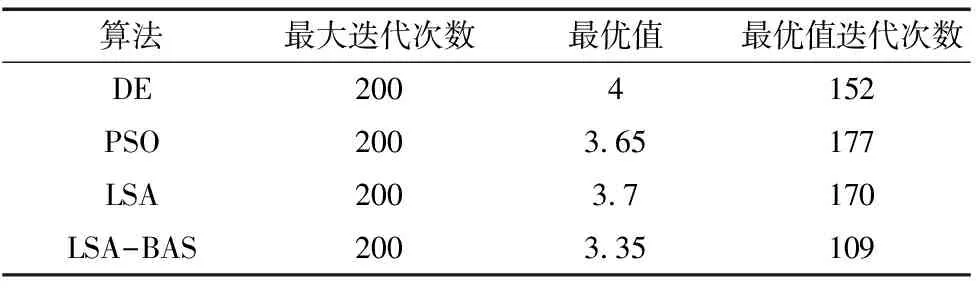
表3 算法結果對比表

圖3 算法收斂曲線

5 結論

LSA算法是一種新的元啟發式算法，LSA算法在求解過程中存在收斂速度較慢、容易陷于局部最優的缺點，針對LSA算法的不足，本文首次提出了把BAS算法中天牛個體的覓食過程融入閃電搜索算法的混合算法，該算法利用BAS算法局部搜索能力較強的特點，使天牛須的感知與閃電粒子的傳播過程相結合，有效的解決了閃電搜索算法易陷入局部最優的問題，加快了算法的收斂速度，提高了算法的搜索精度和全局搜索能力。通過實例驗證和算法對比，該算法在解決裝配序列規劃問題方面具有良好的收斂性能和跳出局部最優的能力。