別讓粗心成為借口

魏蘭

【摘? ? 要】在初中生學習數學的過程中，出現錯誤是不可避免的。因此，對錯誤的分析尤為重要，不能將每次的錯誤都歸結為學生的粗心。其實錯誤也是從另一個角度揭示了學生學習中的思維缺陷。

【關鍵詞】粗心;初中數學;錯誤淺析

中圖分類號：G633.6? ? ? ?文獻標識碼：A? ? ? 文章編號：1006-7485（2021）18-0187-02

Don't Let Carelessness Be an Excuse

——Analysis of Intuitive Errors in Junior Middle School Mathematics

（The Affiliated School of Yong'an No.1 Middle School，China） WEI Lan

【Abstract】In the process of junior high school students learning mathematics， mistakes are inevitable. Therefore， the analysis of errors is particularly important， and each error cannot be attributed to student carelessness. In fact， the error also reveals the thinking defects in students' learning from another angle.

【Keywords】Carelessness; Junior high school mathematics; Error analysis

一、對數學概念理解的膚淺性

由于學生在學習數學的過程中，對一些數學概念或數學原理沒有深刻的理解，僅僅停留在表面概括上，無法把握事物的本質。因此學生在分析和解決數學問題時，往往只善于處理一些直觀的或熟悉的數學問題，而對那些間接使用定理的數學問題，往往不能抓住其本質。

例題一：6a-a=6

對于剛從小學升上初中的學生來說，減去即等于消失，所以這樣的錯誤并不少見，他們沒有意識到6a是6個a，而只是簡單地讓字母a去除。同時，6a減a也涉及合并同類項的概念，正是由具有抽象性的字母計算來代替具體數字的一個重要概念。初中學生正處于經驗型思維到邏輯型思維轉換的過程，無法將抽象的概念運用于實際的題目中，往往做題時還是依賴自己的直觀感知。甚至到了初三，這樣的問題還會出現，個別學生會犯這樣的錯誤，6[2]-6=[2]。

二、僅憑直觀，粗淺判斷

在解決數學問題時，經常會產生一些直覺是正常的，有時還是很可貴的，但是數學是一門嚴謹的科學，產生直覺后還要周密地思考、嚴謹地推理、精密地計算，否則以眼睛的直覺代替理性的思維就很可能會出現錯誤。

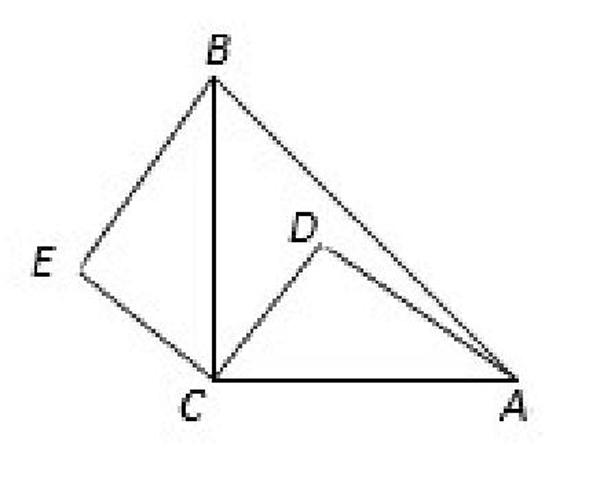
例題二：如圖，在等腰直角△ABC中，∠ACB=90°， D為△ABC內一點，將線段CD繞點C逆時針旋轉90°后得到CE，連接BE，若∠DAB=10°，則∠ABE是 A.75°B. 78° C. 80° D. 90°

因為其中說明了是旋轉線段CD，應該是得到△BEC全等于△ADC，從而得到∠EBC=∠DAC=40°，可是學生只是根據看到圖形，經過最簡單的直觀判斷，選D的人居多。天文學家開普勒曾經說過：“當知識通過感官被直接提供給心靈時，是模糊、混亂和矛盾的，從而也就不可靠的。”教師要時刻教育學生確定事物的本質，不能只靠感覺，應該多一些理性的思考。

三、受思維定式的影響

學生受先前形成的知識經驗、習慣的影響，容易形成認知的固定傾向，從而影響后來的分析判斷，形成思維定式。在環境不變的條件下，定式會使人能夠應用已掌握的方法，迅速解決問題，但是如果環境改變，也會影響人們的創造性。

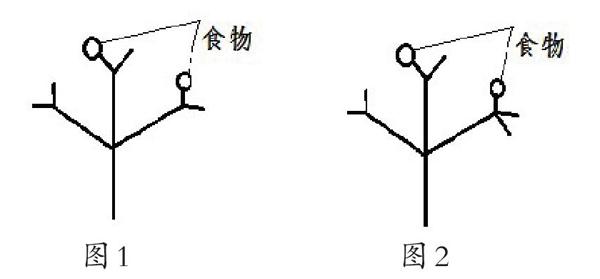
例題三：一只螞蟻在如圖所示的樹枝上尋覓食物，假定螞蟻在每個岔路口都會隨機選擇一條路徑，那么它獲得食物的概率是多少？

圖1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?圖2

圖1和圖2看上去圖形非常類似，只不過圖1有六個樹枝，而圖2有七個樹枝。但是他們的概率卻完全不一樣。圖1找到食物的概率是 [16+16=13]，而圖2找到食物的概率是 [16+19=518]。學生通常用求圖1的概率方法來做第二幅圖的題目，卻得出了[27]錯誤答案。沒有意識到圖1中每個樹枝是等可能性的，而圖2卻不是。學生常常尋求表面上相似的東西，而忽略結構上、本質上的差異，最終導致理解錯誤。因此作為教師要引導學生在學習時，首先應該明白對一個問題不要急于按原先的套路求解，應該從模仿的路子跳出來，避免按部就班，而要先仔細地觀察，學貴存疑，小疑則小進，大疑則大進，這才有可能讓學生針對性地解決問題。

四、知識的負遷移

知識的負遷移是學生形成思維障礙的重要原因，面對一個新的數學問題，學生首先是聯想與之形似或意似、且熟悉的問題，然后遷移解決問題的方法，將當前的問題與頭腦中已有的知識經驗之間建立起某種聯系。這種以類比、聯想為基礎的思維活動，如果伴隨著突破或者創新，那么就是課改所倡導的創新思維能力。如果只是一味地機械照搬，那么思維會呈現呆板，產生錯誤。如學習了有理數加法法則對乘法法則的學習會產生負遷移，學習同底數冪的乘法對冪的乘方產生負遷移。

五、分析問題不夠全面

由于初中學生的年齡小，知識面較為狹窄，邏輯思維能力較為薄弱，分析問題時通常不夠全面細致，而且通常在潛意識中容易出現臆斷，造成解題過程中常常出現顧此失彼的現象。在學生進入初中高年級以后，數學知識點的面加寬、難度明顯增大，而且有些問題已帶有開放性的特征，如果學生一味依靠模仿與死記硬背的學習方法就難以奏效。表現在數學習題的解題中，就是缺少開放性思維方法，思路較為狹窄，往往就是顧此失彼，或者是解答過程簡單化。

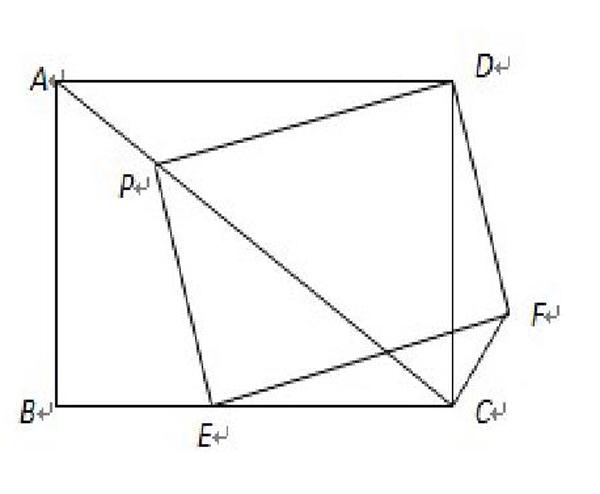
例題四：（17年福建）如圖，矩形[ABCD]中，[AB=6，AD=8] [P，E]分別是線段AC、BC上的點，且四邊形[PEFD]為矩形。

（Ⅰ）若[△PCD]是等腰三角形時，求[AP]的長;

[△PCD]是等腰三角形有三種情況[PC]=[PD]，[CP]=[CD]，[DP]=[DC]但是很多學生會被原題中給出的圖形固定住思維，負略了P、E是可以動的，只考慮了DP=DC。

數學是一門具有高度抽象性和精密邏輯性的科學，思維的嚴密性是學好數學的關鍵之一。教師在授課過程中應該有意識地強調和培養學生思維的嚴密性，不要受現有圖形和既定做法的影響。

六、將圖形當成已知條件

將圖形中出現的貌似的形狀當成條件來解答，這在初中，尤其低年級學生群體中更是屢見不鮮。由于年齡段的特征，初中學生的智力還處于較為低級的階段，對新生事物的認識、理解能力較差，而直觀感知的能力卻較強，他們常常會將圖形中出現的類似等邊三角形、直角三角形的圖形當成已知條件來應用，教師應該及時提醒、糾正，引導學生由形象思維向抽象思維過渡。

例題五：已知：AB是⊙O的直徑，AB=4，∠ABC=30°，D是BC中點且BD=4[3]，過點D作DE⊥AC。求證：DE與⊙O相切。

這道題學生做輔助線通常是連接AD，然后說明因為AB為直徑，所以∠ADB=90°，但是實際上題目沒有任何語句說明點D在圓上，這個結論是需要證明的。但是學生就是將圖中看到的當成了已知條件，想當然地認為，點D已經在圓上了，忽略了對它的證明過程。

上述這些錯誤在學生的數學學習過程中并不少見，學生經常僅靠直觀判斷犯想當然的錯誤，當代科學家波普爾認為：“錯誤中往往孕育著比正確更豐富的發現和創造因素?！币虼私處熢诮虒W過程中應不斷地分析教材、研究學生，將那些容易出錯的問題作為范例，認真上好錯例分析課，直擊要害，讓學生體驗錯誤，探究癥結所在。而且應力爭在課堂上給學生的不是一道題目的正確答案，而是一種思維方法，讓學生發現錯誤的所在以及錯誤發生的原因，從中吸取教訓，舉一反三。在辨析錯因、啟發糾錯的過程中，培養學生思維的嚴密性、廣闊性、深刻性和創造性，讓學生在錯誤中尋求正確的方向，反思錯誤的原因。然后對癥下藥，形成正確合理的認識，找到知識的薄弱環節并盡快彌補，力求在以后的解題中少出現錯誤或不出錯，這也是學生反思成長的過程。

教師應該盡量在教學過程中培養學生的科學理性思維。初中學生的理性思維發展是靠數學來完成的。特別是學生的思維正處于從直觀歸納向邏輯抽象思維轉變的階段。后續的高中數學學習對思維嚴謹性、邏輯性的要求更高，而且數學的理性思維方式遠遠超過了數學試題的本身，廣泛應用于自然科學甚至人文科學和社會科學中，也對學生今后生活長期發揮積極的作用。所以不能只靠眼睛看到的表面現象來直觀判斷事物的屬性，應該學會更深入理智地思考問題的本質，這才是學習數學帶給學生真正的意義。

參考文獻：

[1]王開珍. 初中數學解題錯誤淺析[J].宿州教育學院學報， 2002（02）.

（責編? 侯? 芳）