基于C-Vine Copula下 宏觀經濟指標的相關性研究

劉劍修 戴琳 楊濤

摘要：宏觀經濟指標的變動對我國居民的生活有著重要影響。文章選取1996～2020年的GDP、CPI、第三產業和M2的季度同比增長率數據，利用C-Vine Copula研究這4個指標間的相關性及其尾部依賴特性。研究發現，GDP與其它三個指標相關性最強，第三產業和其它三個指標的相關性次之，而M2和其它3個指標的相關性最弱。

關鍵詞：C-Vine ;Copula;相關性;宏觀經濟指標

一、引言

GDP、CPI是衡量經濟增長和通貨膨脹的重要指標，M2和第三產業是衡量貨幣供應和國家發展水平的重要指標。改革開放40年以來，我國GDP從1978年的3678.70億元增長到2019年的99.09萬億元，增長了近270倍，CPI同樣經歷了多輪漲幅。2013年3月我國M2首次突破百萬億元，僅僅過了7年時間，在2020年1月我國M2突破兩百萬億元。同樣是在2013年，我國第三產業比重首次超過第二產業。

近年來，研究GDP等宏觀經濟的文獻相對較多。王雙正（2009）基于VAR模型，得出通貨膨脹與經濟增長具有雙向的格蘭杰因果關系。周文和趙果慶（2012）利用1996～2009年GDP、CPI及M2增長率的季度數據，建立非線性動力系統模型，得出兩者長期均衡的非線性關系，存在同向變動關系。從現有的文獻來看，對于GDP的研究多數使用計量方法，但傳統的線性相關檢驗在解決非線性相關關系時存在一定的局限性。Copula作為一個“連接”函數，可用于描述變量間的非線性相關關系。王童和雷懷英（2017）用二維Gumbel Copula描述CPI與GDP間的相關關系，得出兩者多數時間保持協同運動。劉曉曉和何華等（2019）用三維Copula函數對CPI與GDP、M3進行相關性分析，得出三者具有正相關性。在Copula的框架下，描述高維變量的相關關系時，常以藤（Vine）的結構形式將高維Copula分解成二維Copula或者條件二維Copula，最常用的藤結構有C藤和D藤。基于以上研究，本文利用C-Vine研究GDP、CPI、M2和第三產業季度同比增速之間的關系。

二、模型的建立

（一）Copula函數

Sklar在1959年提出了Copula理論，該理論指出一個具有一元邊緣分布F1，…，FN的聯合分布函數F一定存在一個Copula函數 C：[0，1]n→[0，1]，且滿足：

F（x1，x2，…，xn）=C（F1（x1），F2（x2），…，Fn（xn））（1）

若（1）式中F1…Fn是連續的，那么C是唯一的。若C是一個Copula，F1…Fn是邊緣分布函數，則由上式定義的F（x1，x2，…，xn）是一個聯合分布函數。

Copula經歷了二維到高維的拓展，在高維的情形下，Bedford和Cooke利用圖形工具”Vine”提出正則藤，將高維Copula分解成二維Copula或者條件二維Copula。不同的分解方式對應著不同的藤結構，最常用的有C藤和D藤。根據其結構特點，本文基于C-Vine進行研究。

（二）C-Vine

一個有n個變量的C藤由n-1棵樹構成，記為T1，T2，…，Tn-1，第i棵樹的節點集記為Ni，邊集記為Ei（i=1，…n-1），它們需滿足以下條件：

1.樹T1的節點集N1={1，2，3…n}，邊集為E1;

2.第i棵樹的節點集和邊集的數量關系為：Ni=Ei-1（1，2，3…n-1）;

3.Ti（i=1，…，n-1）只有一個根節點連接到n-i條邊上。

由定義可知C藤中每棵樹都有一個根節點與其它所有節點相連接，這樣的結構適用于變量之間重要性的排序。本文以四維C藤為例，具體的連接結構如圖1所示：

Cooke提出對于連續分布的隨機向量X=（X1，…，Xd）T，其聯合概率密度函數f（·）可以用二元條件Copula函數和它的邊際密度函數來表示，通過C-vine的特殊結構，可以得到n元C-Vine的聯合密度函數為：

f（x1，x2，…，xn）=∏fk（xk）∏∏Cj，（i-j）|1：（j-1）（Fj|1：（j-1），Fi+j|1：（j-1））（2）

其中fk表示邊緣密度函數（k=1，2，…，n），Cj，i+j|1：（j-1）表示二元Copula密度函數，Fj|1：（j-1）表示條件分布函數Fj|1：（j-1）（xj|x1：（j-1））。

三、C-Vine中根結點及二元Copula的選擇

在C-Vine模型的構建中，每棵樹（Tree）都有一個根節點，因此根節點的選擇是至關重要的。本文采用Czado C提出的方法對根節點進行選擇，步驟如下：

1.假設有n個變量，每個變量有T個觀測值，估計所有觀測變量的相關測度Kendalls，將其記為子贊i，j，i，j=1，2，…n。

2.計算每個變量的Kendalls和，將有最大Kendalls和的變量定義為第一根節點，記為T，排列變量得到T1，Kendalls和的計算方法如下：

子贊i，sum=∑|子贊i，j|，i=1，…，n（3）

3.假設已對T1中的每條邊選擇了合適的Pair-Copula，估計的參數向量為茲贊。根據（3）式估計的參數向量，計算剩下n-1個變量的h函數如下：

ui+1 |1，t=h（ui+1，t|u1，k;茲贊），i=1，…，n-1;t=1，…，n（4）

4.估計n-1個變量的所有Kendalls和，找到使得（3）式最大的變量，定義為第二根節點，記為T。

5.重復以上步驟，直到依次確定所有C-Vine中的根節點。

在確定了每棵樹的根節點之后，本文利用 AIC準則選擇合適的二元Copula。

四、實證分析

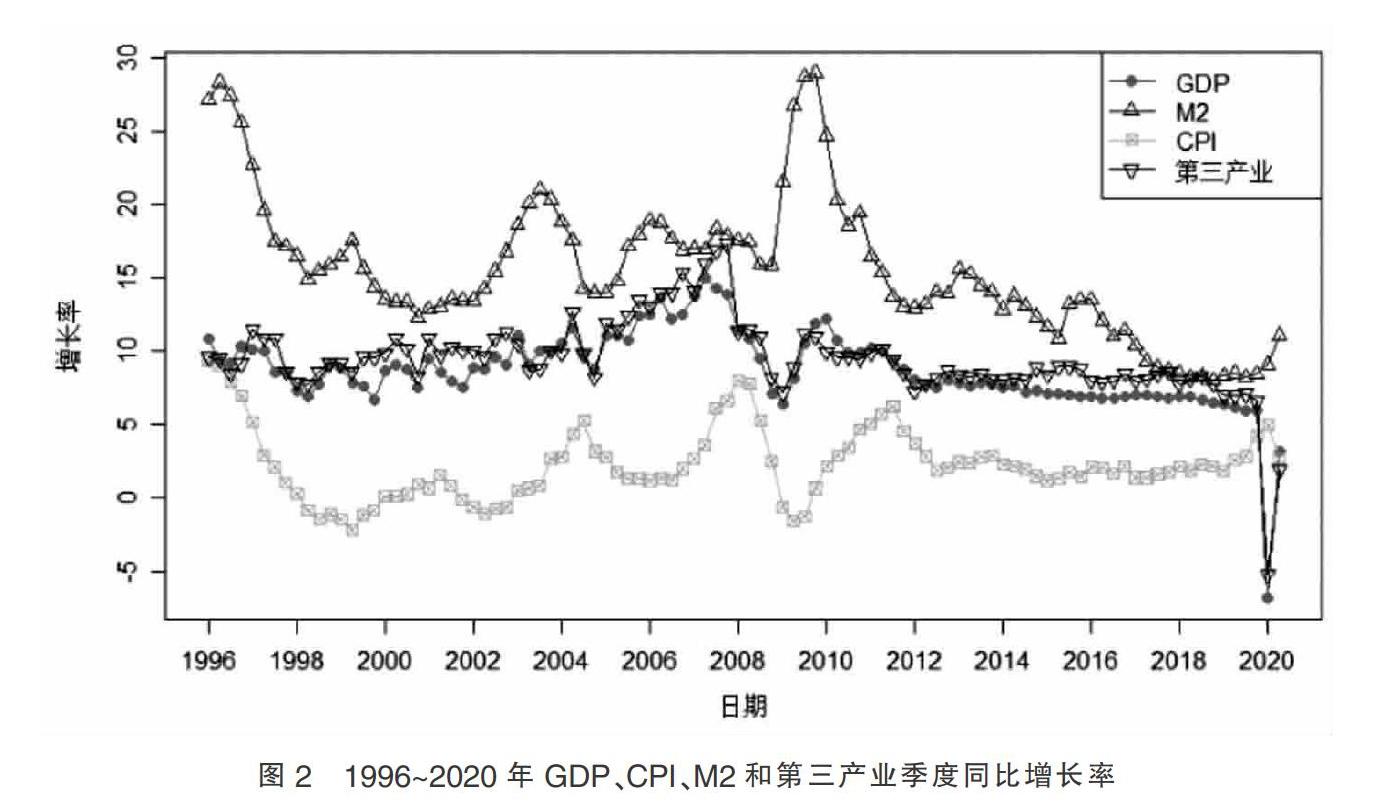
本文基于C-Vine Copula研究GDP、CPI、第三產業和M2季度同比增長率間的相關性及尾部特征，數據來自中經網統計數據庫和國家統計局，時間跨度為1996年1月到2020年6月。該4個指標的季度同比增長率如圖2所示。

從圖2中可以看出，1996～2010年GDP和第三產業的增長保持高度一致，2012～2019年第三產業的增長率明顯高于GDP的增長率，這說明我國的第三產業正快速發展。但在2020年第一季度，我國經濟受到了新冠肺炎的沖擊，GDP首次出現負增長。在國家有力的管控下，在第二季度，我國的GDP實現了正增長。在2008～2010年由于受到全球經濟危機的影響，CPI的增長率出現了較大的波動。從2011年至今，我國的CPI增長率維持較低的增長，處于一個“爬行式”的水平，這屬于正常的物價上升。相比于GDP的增長，廣義貨幣M2的增長處于一個較高的水平，2020年M2的余額已經突破了200萬億元。表1為4個指標增長率的統計特征。

從表中可以得出，1996～2020年GDP和第三產業具有一定程度的左偏，這和近幾年我國經濟的轉型有關，GDP的增速明顯放緩。M2和CPI具有一定程度的右偏，但數值較小。從p值來看，均拒絕正態分布的原假設。

本文的重點是研究GDP與CPI、M2和第三產業增長率間的關系，對數據的邊緣分布不做具體討論，利用累計分布函數將增長率數據轉換為Copula數據，然后用上文介紹的方法選擇合適的C-Vine結構以及二元Copula函數。表2給出了Copula數據的Kendalls和。

從表2中可以得出，GDP的增長率具有最大的子贊sum，因此GDP為C-Vine結構中第一棵樹的根節點。將GDP增長率序列變量記為T，表3給出了已知GDP增長率后的Kendalls和。

從表3中可知，第三產業增長率具有最大的Kendalls和，因此第三產業增長率為C-Vine結構中第二棵樹的根節點。同理，用同樣的方法可以得到CPI為第三棵樹的根節點。

本文對每棵樹每條邊對應的二元Copula進行選擇時，采用AIC準則進行選擇，表4為每條邊對應的Copula以及相應的參數值。

表4中的下標G、D、M、C分別代表GDP、第三產業、M2和CPI的季度同比增長率序列。T1中對應的Copula分別為Gumbel Copula和BB8 Copula。Gumbel Copula函數對變量上尾處分布變化較敏感，說明GDP和第三產業間增長率的分布在上尾處具有很強的相關關系。BB8 Copula為雙參數Copula，它能夠刻畫變量間非對稱的尾部相關關系。T2中對應的二元Copula為Frank Copula，說明在已知GDP增長率的序列后，第三產業與M2和CPI增長率之間具有對稱的尾部特征。T3中對應的二元Copula為Clayton Copula，說明變量間的下尾處具有較強的相關性。根據C-Vine的分解形式，可以得到這4個指標增長率的C-Vine模型為：

C（uG，uD，uC，uM）=CGD·CGC·CGM·CDC|G·CCM|DG（5）

從C-Vine結構可以得出，T1中的根節點為GDP，T2中的根節點為第三產業，T3中的根節點為CPI，CGD為Gumbel Copula;CGC和CGM為BB8 Copula;CDC|G和CDM|G為Frank Copula，CCM|DG為Clayton Copula。因此在這4個宏觀經濟指標中，GDP與其它3個指標的相關性最強，第三產業與其它3個指標的相關性次之，M2與其它3個指標的相關性最弱。

五、結語

本文在Copula的框架下，利用C-Vine結構去捕捉GDP、第三產業、M2和CPI間的相關關系，基于Kendalls和的最大值，對C-Vine的結構進行分解。通過C-Vine的分解形式，可以得到T1中每條邊對應的Copula分別為Gumbel Copula，BB8 Copula，T2中對應的二元Copula均為Frank Copula，T3中對應的二元Copula為Clayton Copula。同時得到M2、CPI、第三產業、GDP與其它3個指標的相關性依次增強。將C-Vine結構的建模方法運用到宏觀經濟指標的相關性研究中，能更好的刻畫變量間的相關性及尾部特征。

參考文獻：

[1]王雙正.基于VAR模型的通貨膨脹與經濟增長關系研究[J].經濟理論與經濟管理，2009（01）：21-27.

[2]周文，趙果慶.中國GDP增長與CPI：關系、均衡與“十二五”預期目標調控[J].經濟研究，2012（05）：5-18.

[3]王童，雷懷英.基于Copula函數的CPI與GDP相關性研究[J].統計與決策，2017（17）：18-21.

[4]劉曉曉，何華，張建.基于三維Copula函數的CPI與GDP、M3相關性研究[J].河北工業大學學報，2019，48（01）：13-17.

[5]戴琳，許東旭，劉慧敏.基于動態Copula-CoVaR系統性風險的評估[J].中國集體經濟，2020（06）：87-92.

[6]Bedford T， Cooke R M. Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines[J].Annals of Mathematics and Artificial Intelligence，2001，32（01）：245-268.

[7]Czado C， Schepsmeier U， Min A. Maximum likelihood estimation of mixed C-vines with application to exchange rates[J].Statistical Modelling，2012，12（03）：229-255.

（作者單位：昆明理工大學理學院。戴琳為通訊作者）