基于應用意識的閩南紅磚拼花中的數學教學思考

陳梅瓊

[摘? 要] 文章結合國家課程標準，以《鋪磚問題》為例，從培養學生應用意識的視角研究閩南紅磚拼花中的數學教學的三大策略：創設生活情境，培養應用意識;探索建構模型，增強應用意識;巧設變式練習，深化應用意識。

[關鍵詞] 應用意識;應用意識培養;紅磚拼花;數學教學

紅磚拼花作為閩南傳統建筑的特色之一，備受閩南人民的喜愛。紅磚拼花中蘊含的數學元素也成為教師積極探索的主題。但閩南紅磚拼花中的數學教學是一個全新的領域，國內外對此領域的研究還是一片空白。我校也是第一次研究此課題，沒有前人的經驗借鑒，研究難度大。因此，在這樣的研究背景下，我們確立了新的視角，探尋新的路徑，對閩南紅磚拼花中的數學注入新的思考，尋找新的著力點，創新教學策略。

數學意識就是指人們以數學為工具對問題進行說明、解釋時，所表現出來的主動性。2011年版課程標準中提出了十個核心概念，應用意識是其中之一，并對應用意識的內涵作了說明：既指能夠運用數學到生活，也指能夠從生活中抽象出數學。在學生的數學素養中，應用意識是重要的內容。應用意識主要體現在：第一，要認識到數學在生活中的應用;第二，能運用數學解決實際問題;第三，能為新的數學知識尋找實際背景。

因此，在應用意識指導下的閩南紅磚拼花中的數學教學，讓學生認識到了紅磚拼花中蘊藏的大量的數學知識，覺得數學知識不再是枯燥無味的，而是如此生動。同時，引導學生運用所學數學知識解決閩南傳統建筑中的問題，培養了學生的數學應用意識。

那么，如何從培養學生應用意識的視角進行閩南紅磚拼花中的數學教學呢？本文將以《鋪磚問題》為例來分析討論其教學策略。

■一、創設生活情境，培養應用意識

數學源于生活，用于生活，高于生活。數學知識是從生活情境中產生的。教學時，教師如果脫離生活情境只教學數學知識，學生可能就只會死背數學公式或數學性質，不明白其中的數學道理，不會靈活運用，更不會運用數學知識解決生活中的問題。因此，教師應創設生活情境展開教學，讓學生在熟悉的生活情境中學習知識，理解數學，體會數學與生活的緊密聯系。這樣，學生對數學學習產生濃厚的興趣，有助于培養學生的數學應用意識。

例如，《義務教育教科書數學》人教版三年級下冊教材第72頁例8《解決問題》一課，是在學生認識了面積的含義，會計算長方形、正方形的面積的基礎上進行教學的。本節課主要是運用面積的含義和除法含義來解決問題。然而，面積的含義對于三年級的孩子來說是非常抽象的。只有結合生活中常見的鋪地磚情境進行教學，讓學生經歷解決問題的過程，感悟利用圖形描述和分析數學問題的方法，積累畫圖幫助理解的學習經驗，才能體會幾何直觀的價值，培養學生的應用意識和實踐能力。

因此，教學時我們巧妙地重組創新教材內容，把閩南傳統建筑中的紅磚文化融入數學課堂，鋪地磚貫穿整節課，課題也改為《鋪磚問題》。在課的導入環節創設這樣的生活情境：

先視頻播放閩南語啟蒙讀物《千金譜》中的童謠：“石條油面磚，石珠石柱雁子磚，瓦壁瓦筒六角磚，六角磚下好花園”。引出紅磚厝最大的特色就是紅磚拼花了，大多數的墻面、地面都采用紅磚拼成的。其實，在閩南建筑鋪磚過程中，還藏著很多數學問題了！

接著課件出示學校的建筑物，向學生介紹：這是我們學校具有歷史意義的老房子，現在學校想把它翻修成校史館，工人叔叔正在給地面作翻修，他們用的地磚就是我們閩南的紅磚。

最后出示主題圖（如圖1）：他們在長是6米，寬是3米的長方形地面，用邊長是3米的正方形地磚鋪地面，一共要用多少塊地磚？

在這樣與生活高度結合的真實情境中，學生更能讀懂題目的意思，更能掌握解決問題的方法。創設這樣的生活情境，不僅激發了學生的學習興趣，而且培養了學生的應用意識。

■二、探索建構模型，增強應用意識

模型思想是數學思想之一，它將數學與現實連接起來。而數學建模就是抽象問題——表示關系——求解結果的過程，貫徹于數學學習的過程中。通過數學模型的建立，可以促進學生理解解決鋪磚問題的方法。教師通過聯系生活，培養學生有意識地將數學模型應用于實際生活問題的解決之中，進一步增強學生的數學應用意識。

在《鋪磚問題》教學中，教師提供了學生最熟悉的生活素材——鋪磚問題，幫助學生尋找數學知識的生活原型，讓學生感受到數學知識在生活中的應用。接著引導學生通過畫圖、思辨、區分解決問題的兩種策略，把知識與生活相聯系，讓學生在感受、學習和理解數學中，感悟數學的魅力，體會了數學的應用價值，增強了學生的應用意識。

【案例再現】

1. 畫簡單的示意圖理解題意。

2. 思考：要求“鋪地面一共需要用多少塊地磚？”要先求什么，再求什么呢？

3. 全班交流算法：

方法一：先算出地面的面積：6×3=18（平方米），再求出地磚的面積3×3=9（平方分米），再求鋪地面一共要用多少塊地磚，用除法：1800÷9=200（塊）。

方法二：先分別算出地面的長和寬可以鋪多少塊地磚：60÷3=20（塊），30÷3=10（塊），再用乘法計算出要用地磚的塊數：20×10=200（塊）。

4. 播放課件：動畫演示兩種方法的鋪地磚過程。

5. 對比兩種方法的異同點。師：上述兩種方法有什么不同？學生比較，找出兩種方法的不同思路與解題步驟。

6. 總結方法，建構模型。

師：請同學們思考一下：解決這一類問題的方法有哪些呢？

學生小組討論，總結出兩種方法：①地面面積÷一塊磚的面積=鋪磚塊數;②長邊鋪的塊數×寬邊鋪的塊數=鋪磚塊數。

教學中，教師將面積問題與實際生活中工人鋪磚的情境完美融合，將數學問題生活化，引導學生用數學的眼光進行思考分析，而后引導學生建立數學模型，培養學生建構數學模型的能力，增強了學生的應用意識。

■三、巧設變式練習，深化應用意識

數學練習不能只關注解題的結果是否正確，更應該重視數學的應用。教師在設計練習時要與學生的生活緊密聯系，注重練習的變式，讓學生靈活運用知識解決問題，深化學生的應用意識。

例如，《鋪磚問題》在新課探究教學后，教師可以設計以下三道變式練習：

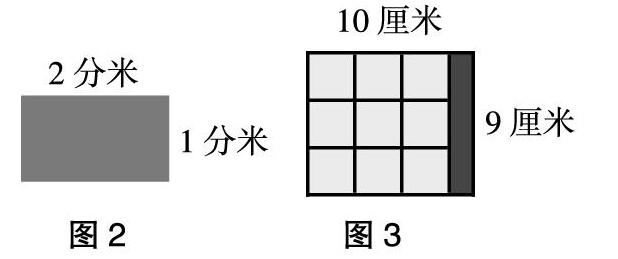
變式練習1：在閩南建筑中，鋪的紅磚不但有正方形地磚，還有其他各式各樣的地磚，這是雁子磚，它是長方形的（如圖2），換成小長方形地磚去鋪地面，地面長8米，寬6米。用長是2分米，寬是1分米的小長方形地磚鋪地面，一共需要多少塊？

變式練習2：在一張長10厘米，寬9厘米的長方形紙上剪邊長為3米的正方形拼花圖案，最多能剪出多少個？

學生解決問題的過程中出現了兩種不同的答案：①大長方形面積是10×9=90（平方厘米），小正方形面積是3×3=9（平方厘米），90÷9=10（個）。②答案是9個，長邊只能剪3個，寬邊正好剪3個，3×3=9（個）。

當學生出現爭議時，教師進一步引導學生討論：到底哪種解法合理呢？學生通過辯論明白了：實際生活中，剩下的小長方形不能剪出一個正方形。通過這道練習題，學生明白了解決問題應該聯系生活實際，對應用意識有了更深刻的理解。

變式練習3：長90米，寬2米的長方形上鋪長為2分米，寬1分米的長方形拼花圖案，鋪這條道路一共需要多少塊？

這里的三道變式練習，學生運用相關的數學知識解決鋪磚問題，既深化了數學知識的應用意識，也更好地鞏固了所學知識，加深了對新知識的理解，讓學生積累了數學學習的成就感。

總之，挖掘閩南紅磚拼花的數學資源進行教學是培養學生應用意識的有效途徑，而加強數學應用又是閩南紅磚拼花教學的最終目的。在閩南紅磚拼花的數學教學中，要創設真實的生活情境，以解決現實的生活問題為依托，引導學生畫圖、探索、思考、辨析、構建數學模型，最后巧妙設計變式練習，運用數學知識解決實際問題，逐步培養學生的數學應用意識。