概括：揭示概念的形成過程

周楊

[摘 ?要] 數(shù)學(xué)概念是教學(xué)的核心，概念教學(xué)要在概念發(fā)生和發(fā)展的過程中揭示其“本來面目”，讓學(xué)生參與概念本質(zhì)特征的概括過程，感悟概念形成的必要性、必然性、合理性.

[關(guān)鍵詞] 概念教學(xué);概括;形成過程;方差

多次觀摩“方差”的教學(xué)，看到的大多是沉悶的課堂，教師往往將方差的概念及計算方式直接告知學(xué)生，教師講得乏味，學(xué)生學(xué)得無趣. 這樣的做法，學(xué)生雖然比較容易掌握方差的概念及其計算方法，但是學(xué)生難以理解為什么要用方差來描述數(shù)據(jù)的離散程度. 這樣的做法體現(xiàn)得更多的是一種記憶認(rèn)識，學(xué)生不會真正掌握日后研究其他描述數(shù)據(jù)的一般方法;這樣的做法生硬、教條，機(jī)械的訓(xùn)練不會讓學(xué)生感受到學(xué)習(xí)的樂趣，不會讓學(xué)生認(rèn)識到探索問題的方法和策略. 概念教學(xué)的關(guān)鍵就是要讓學(xué)生深知建立這個概念的必要性. 方差的教學(xué)價值，就是讓學(xué)生發(fā)現(xiàn)用方差來描述數(shù)據(jù)的離散程度的必要性、必然性、合理性.

內(nèi)容及內(nèi)容解析

1. 內(nèi)容

本節(jié)課為蘇科版九年級數(shù)學(xué)上冊“3.4 方差”的新授課.

2. 內(nèi)容解析

一組數(shù)據(jù)主要描述其集中趨勢和離散程度. 離散程度，即觀測變量各個取值之間的差異程度. 通過對隨機(jī)變量取值之間離散程度的測定，可以反映各個觀測個體之間的差異大小，從而也就可以反映分布中心的指標(biāo)對各個觀測變量值代表性的高低;通過對隨機(jī)變量取值之間離散程度的測定，可以反映隨機(jī)變量次數(shù)分布密度曲線的瘦俏或矮胖程度. 學(xué)生已學(xué)過用平均數(shù)、中位數(shù)、眾數(shù)描述一組數(shù)據(jù)的集中趨勢，本節(jié)課將學(xué)習(xí)如何描述一組數(shù)據(jù)的離散程度. 方差是描述一組數(shù)據(jù)離散程度的重要特征數(shù)，方差越大，數(shù)據(jù)越不穩(wěn)定;它全面、平均地表示一組數(shù)據(jù)的離散程度，是最常用的描述數(shù)據(jù)離散程度的統(tǒng)計量之一，廣泛應(yīng)用于比較實際事物的整體性、均勻性和過程的穩(wěn)定性、均衡性. 方差對學(xué)生統(tǒng)計觀念的形成有著重要的作用.

本節(jié)課的教學(xué)重點是理解方差的概念，會計算簡單數(shù)據(jù)的方差. 為了引導(dǎo)學(xué)生學(xué)習(xí)方差，逐步了解方差產(chǎn)生的必要性與形成過程，理解方差的概念，通過三個層次讓學(xué)生不斷產(chǎn)生認(rèn)知沖突，在認(rèn)知沖突中理解方差. 當(dāng)多組數(shù)據(jù)的平均數(shù)、中位數(shù)、眾數(shù)都相同時，學(xué)生會感受到統(tǒng)計量不夠用，從而形成第一次認(rèn)知沖突，激發(fā)學(xué)生猜想到最大值與最小值的差，即極差. 在原有數(shù)據(jù)的基礎(chǔ)上修改數(shù)據(jù)，當(dāng)平均數(shù)、中位數(shù)、眾數(shù)、極差都相同時，形成第二次認(rèn)知沖突，學(xué)生通過畫圖觀察，得到數(shù)據(jù)波動的大小;為了量化數(shù)據(jù)波動的大小，計算各個數(shù)據(jù)與平均數(shù)的差，當(dāng)發(fā)現(xiàn)差的和為零時，學(xué)生會進(jìn)一步修正為差的絕對值的平均數(shù)，也就是平均差. 繼續(xù)修改數(shù)據(jù)，當(dāng)多組數(shù)據(jù)的平均差也相同時，形成第三次認(rèn)知沖突，此時將絕對值修正為平方，也就是各個數(shù)據(jù)與平均數(shù)之差的平方的平均數(shù)，這樣方差的公式就自然合理地產(chǎn)生了.

在上述整個方差學(xué)習(xí)的過程中，學(xué)生經(jīng)歷了觀察、猜測、計算、驗證等活動過程，充分感悟方差的形成過程，深入理解方差的概念，了解方差產(chǎn)生的必要性. 概念教學(xué)的關(guān)鍵就是要讓學(xué)生深知建立這個概念的必要性，讓學(xué)生掌握研究其他描述數(shù)據(jù)的一般方法，認(rèn)識到探索問題的方法和策略.

目標(biāo)及目標(biāo)解析

1. 目標(biāo)

（1）經(jīng)歷刻畫數(shù)據(jù)離散程度的探索過程，體會方差的統(tǒng)計意義;

（2）掌握方差的概念，會計算簡單數(shù)據(jù)的方差;

（3）了解方差是刻畫數(shù)據(jù)離散程度的一個常用的統(tǒng)計量，并在具體情境中加以應(yīng)用.

2. 目標(biāo)解析

達(dá)成目標(biāo)（1）的標(biāo)志是：在經(jīng)歷畫圖、觀察、探索及量化數(shù)據(jù)離散程度的過程中，體驗方差可以反映數(shù)據(jù)的波動狀況，刻畫數(shù)據(jù)的離散程度，增進(jìn)對方差意義的了解，體會方差的作用.

達(dá)成目標(biāo)（2）的標(biāo)志是：會計算一組數(shù)據(jù)的方差，用方差來描述數(shù)據(jù)的波動程度，進(jìn)一步理解方差的概念.

達(dá)成目標(biāo)（3）的標(biāo)志是：根據(jù)統(tǒng)計的結(jié)果，對具體數(shù)據(jù)的集中趨勢、離散程度做出簡單的判斷，對事例數(shù)據(jù)的發(fā)展變化做出簡單的預(yù)測.

3. 教學(xué)問題診斷

由于學(xué)生剛剛學(xué)習(xí)了數(shù)據(jù)的集中趨勢，學(xué)生可能會習(xí)慣于用所學(xué)的平均數(shù)、中位數(shù)、眾數(shù)去解決生活中的統(tǒng)計問題，所以研究數(shù)據(jù)波動的必要性需要學(xué)生充分體會. 由于方差的計算公式較復(fù)雜，學(xué)生難以記憶，而且為什么要這么算、方差公式的合理性也使得學(xué)生疑惑不解. 正是理解的困難造成記憶、計算和應(yīng)用的困難，這些都需要教師在遵循學(xué)生的認(rèn)知規(guī)律的基礎(chǔ)上借助典型實例加以說明. 在具體的實例中，若數(shù)據(jù)較多較大，則會影響學(xué)生的探究樂趣，故在選取實例時不宜選用數(shù)據(jù)較多較大的實例. 在對統(tǒng)計的結(jié)果進(jìn)行解釋時，受以前數(shù)學(xué)學(xué)習(xí)結(jié)果的是非判斷原則的影響，學(xué)生容易將統(tǒng)計的結(jié)果以簡單的“對錯”為判斷標(biāo)準(zhǔn). 因此在實際情境中，不能合理選擇統(tǒng)計量進(jìn)行分析，對于統(tǒng)計結(jié)果不會有合理的解釋. 基于以上分析，確定本節(jié)課的教學(xué)難點是了解方差產(chǎn)生的必要性和形成過程，體會方差算法的合理性.

教學(xué)過程設(shè)計

1. 創(chuàng)設(shè)情境，引入極差

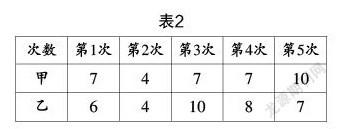
甲、乙兩位運動員在射擊選拔比賽中，各射擊了5次，成績?nèi)绫?所示（單位：環(huán)）.

問題1 ?現(xiàn)在要選派一位運動員去參加比賽，如果你是教練，你準(zhǔn)備怎么辦？用數(shù)據(jù)表達(dá)你的觀點.

追問 ?我們發(fā)現(xiàn)平均數(shù)、中位數(shù)、眾數(shù)都一樣，無法選擇. 為了穩(wěn)中求勝，我們要研究兩位運動員的穩(wěn)定性. 你能看出誰更加穩(wěn)定嗎？用數(shù)據(jù)表達(dá)你的觀點.

師生活動 ?教師提出問題并引導(dǎo)學(xué)生思考，用數(shù)據(jù)闡明自己的看法. 學(xué)生計算兩組數(shù)據(jù)的平均數(shù)、中位數(shù)、眾數(shù)后，發(fā)現(xiàn)這三個量都是一樣的，此時產(chǎn)生了認(rèn)知沖突，由此激發(fā)學(xué)生去尋找另一種量來描述甲、乙兩位運動員射擊成績的優(yōu)劣. 學(xué)生經(jīng)過小組合作交流，想到用最大值減去最小值，也就是用極差來描述，由此引出本節(jié)課的主題：描述數(shù)據(jù)離散程度的量.

設(shè)計意圖 ?聯(lián)系生活實際，激發(fā)學(xué)生的學(xué)習(xí)興趣. 以兩名運動員的射擊成績創(chuàng)設(shè)情境——兩組數(shù)據(jù)的平均數(shù)、中位數(shù)、眾數(shù)都相同，設(shè)置為5次成績，簡化計算，易于探究. “問題1”復(fù)習(xí)了平均數(shù)、中位數(shù)、眾數(shù)在生活中的應(yīng)用，“追問”讓學(xué)生理解僅用平均數(shù)、中位數(shù)、眾數(shù)不能解決射擊問題，它需要更多的描述數(shù)據(jù)的統(tǒng)計量，讓學(xué)生感受到研究數(shù)據(jù)的必要性.

2. 問題探究，引入方差

問題2 ?如果改變數(shù)據(jù)，平均數(shù)、極差都相同，還可以用什么量來描述數(shù)據(jù)的離散程度？

追問1 ?以射擊次數(shù)為橫坐標(biāo)，對應(yīng)成績?yōu)榭v坐標(biāo)，在平面直角坐標(biāo)系中描點. 觀察圖像，你能發(fā)現(xiàn)什么特征？

追問2 ?每次成績相對于平均數(shù)的波動大小是多少？可以用什么量來描述？

追問3 ?兩組數(shù)據(jù)的個數(shù)不一樣，怎么辦？

師生活動 ?教師提出問題并引導(dǎo)學(xué)生思考，若還是不能解決問題，再通過追問引導(dǎo)學(xué)生思考，既然從數(shù)的角度無法研究，可以借助形來研究. 通過“追問1”的引導(dǎo)，學(xué)生很容易描出對應(yīng)的點，實際教學(xué)中大多數(shù)學(xué)生會將這些點連成折線圖. 學(xué)生觀察折線圖后會發(fā)現(xiàn)點的上下波動，此時引導(dǎo)學(xué)生觀察這些點在幾環(huán)附近波動，并通過“追問2”讓學(xué)生用一個統(tǒng)計量量化每個數(shù)據(jù)波動的大小. 學(xué)生由此會想到每個數(shù)據(jù)波動大小的和. 通過“追問3”——如果兩組數(shù)據(jù)的個數(shù)不同，由此激發(fā)學(xué)生想到平均差.

設(shè)計意圖 ?改變數(shù)據(jù)，在平均數(shù)、極差都相同的情況下，激發(fā)學(xué)生思考描述數(shù)據(jù)離散程度的其他量. 通過“追問1”引導(dǎo)學(xué)生在動手畫圖中集思廣益，用圖直觀研究成績分布情況，為下一步定量的研究做好準(zhǔn)備. 通過“追問2”引導(dǎo)學(xué)生思考畫圖除了能直觀反映數(shù)據(jù)的波動外，還能將其量化，體現(xiàn)定性到定量的分析過程.

問題3 ?如果改變數(shù)據(jù)，平均數(shù)、極差、平均差都相同，還可以用什么量來描述數(shù)據(jù)的離散程度？

追問 ?與絕對值功能類似的是什么量？

師生活動 ?此時學(xué)生已經(jīng)得到描述數(shù)據(jù)離散程度的一個量（平均差），為了引導(dǎo)學(xué)生想到方差，繼續(xù)改變數(shù)據(jù)，使得平均數(shù)、極差、平均差都相同，激發(fā)學(xué)生在得到平均差的基礎(chǔ)上再次優(yōu)化描述數(shù)據(jù)離散程度的表示方法，通過“追問1”引導(dǎo)學(xué)生想到平方，由此引出方差的概念.

設(shè)計意圖 ?改變數(shù)據(jù)，在平均數(shù)、極差、平均差也都相同的情況下，進(jìn)一步激發(fā)學(xué)生思考描述數(shù)據(jù)離散程度的其他量，通過“追問”引導(dǎo)學(xué)生發(fā)現(xiàn)與絕對值功能類似的平方，進(jìn)而得到方差. 進(jìn)一步感受并理解用方差描述數(shù)據(jù)波動大小的合理性.

3. 回顧反思，形成概念

回顧以上探索過程：①一組數(shù)據(jù)中每個數(shù)據(jù)與平均數(shù)的差;②差的平方和;③差的平方的平均數(shù). 將上述過程歸納呈現(xiàn)：

用途：方差是描述數(shù)據(jù)離散程度的一個量. 一組數(shù)據(jù)方差越小，數(shù)據(jù)波動越小;方差越大，數(shù)據(jù)波動越大.

設(shè)計意圖 ?讓學(xué)生在教師的引導(dǎo)下感受新知，通過合作交流，得到方差的本質(zhì)特征，獲取新知，體會方差的統(tǒng)計思想.

4. 應(yīng)用概念，解決問題

例 某市2018年、2019年3月前5日的日最高氣溫（單位：℃）如下（見表4）：

該市這兩年中，哪一年3月前5日的日最高氣溫比較穩(wěn)定？為什么？

師生活動 ?學(xué)生獨立思考、計算、判斷，解決問題;教師展示學(xué)生的解答過程，引導(dǎo)學(xué)生分析題意、規(guī)范書寫. ?重點要理清以下幾個問題：①題目中“穩(wěn)定”的含義是什么？說明在這個題目中要研究一組數(shù)據(jù)的什么特征？②在求方差之前先要求哪個統(tǒng)計量？總結(jié)用方差估計數(shù)據(jù)離散（波動）程度的步驟.

設(shè)計意圖 ?鞏固方差公式，再一次體驗方差在生活中的應(yīng)用，結(jié)合實例理解方差的意義，熟悉公式的計算過程——先計算平均數(shù)，再求差，平方后再求平均數(shù)，進(jìn)而規(guī)范解題格式.

練習(xí)1 ?某地某日最高氣溫為12 ℃，最低氣溫為-7 ℃，該日氣溫的極差是______.

練習(xí)2 ?為了從小明和小剛兩人中選拔一人參加射擊比賽，現(xiàn)對他們的射擊成績進(jìn)行了測試，5次打靶命中的環(huán)數(shù)如下：小明是7，8，7，8，10;小剛是10，4，10，6，10.

（1）填寫表5：

（2）根據(jù)以上信息，若教練選擇小明參加射擊比賽，理由可能是什么？

（3）若小剛再射擊2次，分別命中7環(huán)、9環(huán)，則小剛這7次的射擊成績的方差_________. （填“變大”“不變”或“變小”）

（4）根據(jù)以上信息，若教練選擇小剛參加射擊比賽，理由可能是什么？

師生活動 ?教師呈現(xiàn)練習(xí)題，學(xué)生獨立完成. “練習(xí)2”的第（2）問要強(qiáng)調(diào)平均數(shù)相同，可舉例進(jìn)一步讓學(xué)生理解為什么要平均數(shù)相同. 如甲的5次射擊成績是6，6，6，6，6，方差為0;乙的5次射擊成績是6，7，8，9，10，方差為2. 甲的方差小，但成績明顯不如乙. 本節(jié)課主要研究方差這種在統(tǒng)計中常用的刻畫數(shù)據(jù)離散（波動）程度的統(tǒng)計量，在用方差分析數(shù)據(jù)的波動程度時，只適用于在平均數(shù)相同或相近的情況. “練習(xí)2”的第（3）問引導(dǎo)學(xué)生思考，除了直接計算小剛7次成績的方差，還可以怎么算;“練習(xí)2”的第（4）問引導(dǎo)學(xué)生發(fā)現(xiàn)，有的時候并不是數(shù)據(jù)的方差越小越好，應(yīng)該根據(jù)情況而定，教師可以舉出適當(dāng)、簡單的例子來說明.

設(shè)計意圖 ?“練習(xí)1”是鞏固極差;“練習(xí)2”的第（1）問是計算平均數(shù)與方差，進(jìn)一步鞏固方差的計算方法;“練習(xí)2”的第（2）問是體驗方差在生活中的應(yīng)用，進(jìn)一步體會用方差刻畫數(shù)據(jù)的波動程度;“練習(xí)2”的第（3）問結(jié)合實例進(jìn)一步理解方差的本質(zhì);“練習(xí)2”的第（4）問表示在實際問題中，不一定是數(shù)據(jù)的波動程度越小越好.

5. 小結(jié)思考，深化認(rèn)識

（1）什么是方差？

（2）方差有什么作用？

（3）如果兩組數(shù)據(jù)的平均數(shù)、極差、平均差、方差都一樣，又用什么量來描述數(shù)據(jù)的離散程度？

設(shè)計意圖 ?“問題（1）”引導(dǎo)學(xué)生回顧方差的計算公式;“問題（2）”引導(dǎo)學(xué)生思考方差的統(tǒng)計意義;“問題（3）”激發(fā)學(xué)生繼續(xù)探索描述數(shù)據(jù)離散程度的統(tǒng)計量.

教學(xué)反思

概念教學(xué)要在概念發(fā)生和發(fā)展的過程中揭示它的“本來面目”，讓學(xué)生參與概念本質(zhì)特征的概括過程，感悟概念形成的必要性、必然性、合理性. 本節(jié)課似乎沒什么內(nèi)容可講，也沒什么難點，很容易完成教學(xué)任務(wù)，但這只是知識目標(biāo)的實現(xiàn). 方差概念的重要性不言而喻，要讓學(xué)生感受到數(shù)學(xué)概念產(chǎn)生和發(fā)展的基本過程，體會到研究數(shù)學(xué)問題的基本套路，進(jìn)而提高提出問題、研究問題的能力，才算體現(xiàn)方差概念的教學(xué)價值.

1. 讓概念在沖突中產(chǎn)生

概念的形成過程充滿了矛盾和沖突，這是激發(fā)學(xué)生學(xué)習(xí)興趣與熱情的內(nèi)在條件. 本節(jié)課中，刻畫數(shù)據(jù)波動程度的統(tǒng)計量常有極差、方差、標(biāo)準(zhǔn)差、平均差、四分位差等. 方差是描述一組數(shù)據(jù)離散程度的重要特征數(shù)，而學(xué)生已經(jīng)學(xué)習(xí)過描述集中趨勢的特征數(shù)有平均數(shù)、中位數(shù)、眾數(shù)，這些都是統(tǒng)計分析中重要的參考數(shù)據(jù)，所以學(xué)生在分析一組數(shù)據(jù)時會很自然地以上述三個特征數(shù)作為切入點. 在初始階段，教師給出兩組平均數(shù)、中位數(shù)、眾數(shù)都相同的數(shù)據(jù)，讓學(xué)生分析數(shù)據(jù)并做出合理決策，此時學(xué)生會產(chǎn)生第一次認(rèn)知沖突. 在問題分析階段，教師通過改變數(shù)據(jù)，使得兩組數(shù)據(jù)的平均數(shù)、極差都相同，營造第二次認(rèn)知沖突. 在問題解決階段，教師繼續(xù)改變數(shù)據(jù)，使得兩組數(shù)據(jù)的平均數(shù)、極差、平均差也都相同，營造第三次認(rèn)知沖突. 每次認(rèn)知沖突使得尋找另一種統(tǒng)計量成為進(jìn)一步研究的方向，由此自然地引入方差，這是一種無聲的數(shù)學(xué)交流. 學(xué)生在層層深入的問題的引領(lǐng)下，很快會對問題理解得更加透徹. 在這三個階段中，不斷營造認(rèn)知沖突，讓概念在解決問題的有沖突的過程中產(chǎn)生.

2. 讓概念在概括中形成

使概念課生動活潑、優(yōu) 質(zhì)高效的關(guān)鍵之一是讓學(xué)生參與概念本質(zhì)特征的概括過程. 這就要求我們充分利用新舊知識蘊含的矛盾，激發(fā)認(rèn)知沖突，把學(xué)生卷入其中，讓學(xué)生有參與的時間和機(jī)會，特別是要有實質(zhì)性思維的參與. 讓概念在沖突中產(chǎn)生，目的是給學(xué)生參與概括概念本質(zhì)特征的機(jī)會，實實在在地經(jīng)歷概念的形成過程. 如本節(jié)課的探究過程，必然要從數(shù)和形兩個方面展開思考，于是差就很容易被概括了出來，平均差、方差等概念的產(chǎn)生也比較自然. 教師適時介入，強(qiáng)化本質(zhì)特征，規(guī)范概念的表達(dá)，與學(xué)生一起完成概念的定義. 課堂小結(jié)構(gòu)建了一個新的問題，學(xué)生可以從中學(xué)習(xí)如何獲得研究的對象、如何提出研究的問題、如何找到研究的方法. 這些都是課本中找不到的，需要學(xué)生具有一定的概括能力.

3. 讓概念形成過程自然

概念課就應(yīng)該使概念形成得自然、應(yīng)然、必然. 本節(jié)課的教學(xué)，力求使學(xué)生了解方差概念的背景和形成過程，了解為什么要引入這個概念，怎樣定義這個概念，怎樣入手研究一個新的課題. 從課堂教學(xué)的要求來看，概念教學(xué)的自然、應(yīng)然、必然包括兩方面：一是知識的邏輯順序，二是學(xué)生的心理邏輯，主要是思維過程. 在引導(dǎo)學(xué)生展開對相關(guān)概念進(jìn)行學(xué)習(xí)的過程中，要讓學(xué)生參與概念的概括活動，不輕易打斷學(xué)生的思維和行動，恰時恰點地以問題引導(dǎo)學(xué)生在“追問—反思”的過程中深化對概念的理解，使學(xué)生對概念的理解成為他們主動思維的結(jié)果. 因此，本節(jié)課對方差概念的教學(xué)，為學(xué)生勾勒了研究框架和總體思路，使學(xué)生知道往哪里走，引導(dǎo)學(xué)生在不斷的認(rèn)知沖突中理解方差的定義、方差的表示. 概念教學(xué)要返璞歸真，在概念發(fā)生和發(fā)展的過程中要揭示它的“本來面目”;要讓學(xué)生參與概念本質(zhì)特征的概括過程，這是概念教學(xué)中培養(yǎng)學(xué)生的創(chuàng)新精神和實踐能力的必由之路.

3123501908212