“再創造”范式下的一題一課復習

胡柳青

[摘 ?要] 學習數學的唯一正確方法是實行“再創造”，也就是學生要學習的東西由自己去發現或創造出來. 教師的任務是引導和幫助學生進行這種“再創造”的工作，而不是把現成的知識灌輸給學生. 文章以“反比例函數k的幾何意義”為例，結合一題一課復習詳盡地展現了這一范式操作的可行性和科學性，闡述實際操作中如何謀篇布局，提質促效.

[關鍵詞] 再創造;一題一課;數學復習

問題提出

弗賴登塔爾反復強調：學習數學的唯一正確方法是實行“再創造”，也就是學生要學習的東西由自己去發現或創造出來. 教師的任務是引導和幫助進行“再創造”的工作，而不是把現成的知識灌輸給學生. 因此，進行有指導的“再創造”無可非議是每個數學教育工作者必須領會和遵循的教學思想.

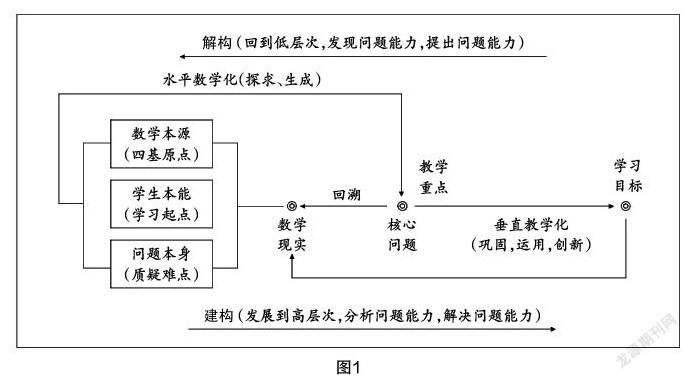
省特級教師、正高級教師盛志軍于2017年成立桐廬縣、富陽區杭州市農村名師工作室. 工作室以弗賴登塔爾的“再創造”理論為指導，開展《再創造：基于核心素養的初中數學課堂范式研究》的課題研究（浙江省教研規劃課題G2019028）. “再創造”教學范式顯著特征就是強調學生再創造者的地位，經歷知識的再創造過程，注重與生活的聯系和應用. 根據弗氏相關理論，我們把“再創造”教學的基本理念描述如下（如圖1）：

（1）確定處于學術狀態的“現成數學”中的核心內容作為教學材料;

（2）把核心問題回溯到學生的現成數學狀態中去，進而發現問題、提出問題、理解問題;

（3）引領學生數學認知聯結（尋求興趣點、生長點和疑難點等），通過“水平數學化”分析問題，初步解決核心問題;

（4）鞏固核心內容，并以此為起點，“垂直數學化”，拓展探索，發現新的問題，水平探索……螺旋上升，循環往復.

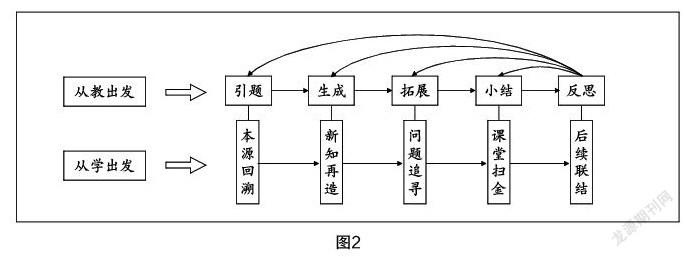
三年來，工作室開展了豐富多彩的實踐活動，就如何實施“再創造”教學進行有益探索并構建基本范式（如圖2）. 《反比例函數k的幾何意義》為工作室成員盧老師的一堂示范課，現摘錄如下，以饗同仁.

課例展示

1. 復習課題

反比例函數k的幾何意義.

2. 復習目標

（1）經歷從函數圖像上任意一點向x、y軸作垂線所得三角形（矩形）面積的探索過程，進一步理解函數系數k的幾何意義.

（2）通過探究函數系數k的幾何意義，感受數形結合和轉化等數學思想、數學方法.

（3）能夠靈活運用函數系數k的幾何意義，解決一些比較綜合的問題，理解函數系數k的本質.

3. 學情分析

浙教版教材中，學生在八上學習函數、一次函數，在八下學習反比例函數，在九上學習二次函數，在九下學習三角函數等. 反比例函數學習，可以促進學生進一步理解函數概念，熟悉研究過程與思考方法，為后續學習奠定基礎. 在學習中，學生對于函數解析式等理解相對透徹，對幾何意義的理解尚顯不足. 反比例函數的問題解決，通常會與圖形面積交匯一起，通過對應關系滲透數形結合思想，從而理解函數系數k、函數解析式和函數圖形的內在聯系，建立“數”“式”“形”的一一對應關系. 為此，本節課將在原有模型基礎上構建新模型，通過水平數學化和垂直數學化，激發學生更深層次的思維活動，實現反比例函數k的幾何意義的“再創造”學習. 本節課確定如下幾點.

中心：反比例函數k的幾何意義;

重心：反比例函數k的幾何意義的綜合問題探究;

核心：反比例函數中數形結合思想的運用.

4.思考方向

函數背景考點多. 反比例函數知識繁雜，需要熟練掌握概念、圖像、性質與應用等. 知識間不是獨立存在的，往往相互聯系，綜合程度比較高. 反比例函數已然成為中考的常考內容，形式越來越新穎，探索性越來越強. 本節課以反比例函數系數k為突破口，探究其與矩形、三角形面積的內在聯系，將知識進行整理、融合、提升，對學生分析和解決問題的能力提出更高要求.

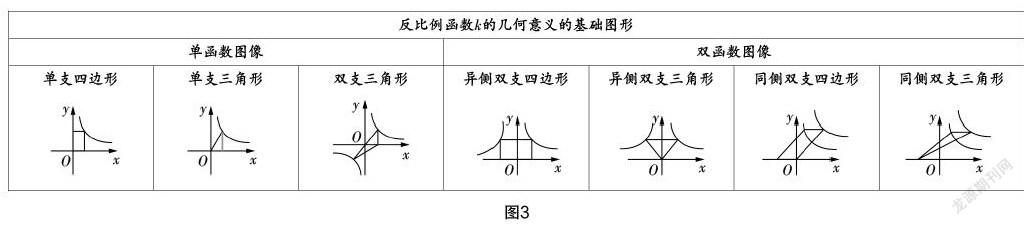
圖像變化種類多. 利用k的幾何意義解決反比例函數與面積的綜合問題，通常會在基礎圖形（見圖3）上變化延伸，從而產生更多圖形. 如何在眾多變形中找出內在聯系，進而有效解決，就需要他們熟練掌握基礎圖形，概括歸納尋求共性，進而找出通解通法.

思維提升阻礙多. 反比例函數是最基本的初等函數，是學習二次函數、三角函數乃至對數與指數函數的基礎，系數k與生俱來的代數意義和幾何意義，完美體現了“數形結合”. 已知系數k，就應該聯想到相關圖形面積，考慮系數k的幾何意義;反之，如果知道相關面積信息，就應該考慮系數k的代數意義. 學習時，學生們往往會割裂其聯系，顧此失彼. 這就需要教師引導學生打破原有的知識壁壘，從復雜圖形中抽絲剝繭地找出基礎模型，尋找解決問題的鑰匙，實現“再創造”的學習.

基于以上分析，本節課將通過模型來研究題型，依托一題多解和多題一解，對反比例函數系數k的幾何意義進行再次理解和歸納，從而實現知識、技能和思想方法上的“再創造”.

5. 設計思路

環節一 ?本源回溯

（1）我們已經學過一次函數、反比例函數和二次函數等知識，請思考：

問題1：平面直角坐標系上有一點A（1，6），你能得到過點A的函數嗎？如果有點A（1，6）和點B（2，3），你能得到過點A，B的函數嗎？如果有點A（1，6）、點B（2，3）、點C（-1，-6），你能得到過點A，B，C的函數嗎？

問題2：①如圖4，如果有點A（1，6）、點B（2，3）、點C（-1，-6）和點D（-2，-3），你能得到過點A，B，C，D的函數嗎？你能找出圖像上的其他點嗎？

②如圖5，在函數圖像上，過點B向x，y軸作垂線，垂足為E，F，則OEBF面積為多少？若P（x，y）是圖像上任意一點，過點P向x，y軸作垂線，垂足為M，N，則OMPN面積為多少？

③如圖6，過點A，B，C，D作x軸（或y軸）垂線，該點、垂足與點O構成四個三角形，求三角形面積. 如果P是函數圖像上任意點，作x軸（或y軸）垂線，求垂足、點P、點O所構三角形面積.

設計說明：本源回溯是整個課堂教學的基礎，務須符合認知需求，強調知識銜接. 教師從經過一個、兩個、三個、四個點的解析式入手，從本源上引導學生回溯系數k與幾何面積的聯系，關注k的代數意義與幾何意義. 只有本源回溯精準，才能從學生實際出發，開展適合學生認知的學習，以此來加強教學活動設計的實效性，為“再創造”提供可行條件.

環節二 ?新知再造

設計說明：新知再造要引導學生梳理知識網絡，在整體結構中理解數學本質. 學生認知結構、活動經驗等均有不同，有獨特“數學現實”. 教師課堂教學“再創造”，要根植學生的“數學現實”和“思維水平”，創設豐富的學習活動，分別經歷知識的水平數學化和垂直數學化，完成“再創造”，達成知識建構. 拓展一，先求出點A，B，延長BO交另一支于點C，如圖14，利用對稱性得BO=CO，△AOB與△AOC面積相等，求得△AOB面積. 拓展二，由一支曲線上兩點轉化為兩支曲線的特殊點，如圖16，連接OA，OB，得S△APB=S△AOB，利用模型求得S△APB=S△AOB=S△AOC-S△BOC=2. 拓展三，將特殊點又轉化為一般點（如圖18），將同一象限的兩點轉化為不同象限的兩點（如圖20、22），仍可用類似方法求解：問題1，如圖19，過A，B作x軸垂線AM，BN，轉化為四邊形與三角形面積的和（差）：S△AOB=S△AOM+S四邊形AMNB-S△OBN，與例題不同的地方是：由于點在不同函數上，故兩個三角形面積不相等;問題2則與拓展一完全相同，可利用中心對稱性，如圖21，延長BO交雙曲線另一支于點C，得S△ABO=S△ACO;問題3則與前兩問題的解法相似，如圖23，轉化為四邊形與三角形面積的和（差）. 教師逐步引導下，找出問題共性，一題多解，多題一解，體會利用基礎模型解決復雜問題的便利，最終實現數學知識和思想方法的“再創造”.

設計說明：后續聯結是整節課的知識回顧，也可以是下節課的本源回溯，但不能和預習與復習混淆. 后續聯結是鞏固所學知識、形成技能方法、培養良好思維、發展核心素養的重要途徑. 問題選擇時也要適當提升難度，培養發散思維，提升創新思維，在持續發展中不斷“再創造”. 上述題目均選自2020年中考真題，著重考查學生是否掌握了反比例系數k的幾何意義，起到課后檢測的作用.

反思跟進

“再創造”范式下的一題一課復習，是一個讓學生在更高視野下的構建知識的過程，也是一個讓學生在更深思維下的感受生長的過程，還是一個讓學生在更精文化下的發展自我的過程. 本節課從一個主問題開始，以點帶面、由淺入深地復習整章知識，通過反比例函數k的幾何意義串聯形成一條主線，不同的知識又由這條主線關聯在一起，從而使得復習教學走向簡約而高效.

1. “再創造”范例下的一題一課，要選準一個好題

數學復習應該有一定的廣度和深度. 廣度是橫向上的容量與范圍，深度則是縱向上的數學思考. 一題一課，知識的掌握、方法的提升、思想的領悟都凝聚于題，一題的選擇就尤其關鍵. 首先，知識內容應該是主干知識、重要思想，而不能旁枝逸出，輕重不分;其次，知識含量應該充足，或者可供拓展，能進行豐富和必要的發散提升;最后，知識種類應該豐富，是多種類、多樣化的，既要有知識、技能，又要有思想、方法和活動體驗. 教學時還要對所選例題進行充分的、必要的、精細的打磨，要將所選問題與教學目標進行關聯，弱化無關知識，強化核心思想，從而保證最終解決的問題具有很高的價值.

2. “再創造”范例下的一題一課，要突出一個主體

《義務教育數學課程標準》指出“有效的教學活動是學生學與教師教的統一，學生是學習的主體，教師是學習的組織者、引導者與合作者”. “再創造”范例下的一題一課就是要強調“學生之本位”，還“課堂之本色”. 教學中，要始終以學生為主體，嘗試引導學生參與變式、擬題活動，提出一些富有探究價值的問題，在問題中提升，使得學生對知識理解更為全面、更加透徹，讓不同層次學生有不同程度的理解深度，讓個性相異學生表達自主獨特的思考路徑，還要讓學生的疑惑引發教師的思考，將被動灌輸轉變為主動探究，從而將復習教學轉化為生動有趣、學知育人的有效課堂.

3. “再創造”范例下的一題一課，要經歷一次生長

教育的出發點和落腳點就是讓學生經歷成長、見證成長、完成成長. “再創造”范例下的一題一課復習秉承的是一種讓學生在復習課中成長的理念，講究的是一種讓學生在復習課中成長的策略. 具體地講，“再創造”范例下的一題一課，正是通過創設問題情境、獨立自主探究、生生合作交流、師生成果展示等過程，讓學生充分經歷觀察、類比、猜想、思考、驗證、推理、轉化等過程，讓他們感受到數學可以如此有趣、輕松地學，而且能夠理解與掌握研究數學、解決問題的常用思路和一般方法. 唯有如此，才能讓核心知識、重要思想的真正價值落到實處，也只有這樣，才能確保教學方向的準確無誤，學習成效的顯著提升，才能真正激發學生的數學學習興趣，啟迪數學智慧，開拓思維能力，培養創新意識，提高數學素養.

以往，在浩瀚的圖書館中尋找多日的資料，今天，借助百度、知乎可以信手拈來;以往，“知識就是力量”，未來，“思維才是力量”;以往，在職場中穩操勝券的是“有知識的人”，未來，在職場中獨領風騷的將是“會學習的人”……“再創造”就是讓學生參與發現、探索、創造知識的全過程. 只有教師“再創造”地教才能為學生“再創造”地學提供肥沃土壤，才能使學生的“再創造”能力不斷地得到發展.