基于MKT理論的初中數學教學設計新探

杜曉婷

【摘要】MKT理論是由美國密歇根州立大學教授鮑爾及其團隊提出的，該理論立足于數學學科，從數學的角度做數學教育研究.本文基于MKT理論在初中數學教學設計中的應用，探索和思考如何培養學生的數學核心素養.基于MKT理論的教學設計分析有助于教師厘清教材思路，有效把握教學內容;有助于學生對知識的深度理解，符合學生的認知規律.

【關鍵詞】初中數學;教學設計;MKT理論

一、MKT理論的內涵

MKT理論（Mathematical Knowledge for Teaching），意為面向教學的數學知識，是由美國密歇根州立大學教授鮑爾及其團隊提出的，該理論認為數學教師不僅應具備學科知識，而且應具備和學科教學相關的知識.該理論分為兩大類：學科知識（SMK）與學科教學知識（PCK）.其中學科知識又由一般內容知識（CCK）、專門內容知識（SCK）、數學水準知識（HCK）三部分組成;而學科教學知識則由內容與學生的知識（KCS）、內容與教學的知識（KCT）以及內容與課程的知識（KCC）組成.筆者認為MKT理論很好地解釋了教師有效教學需要的知識結構，六個成分全面涵蓋了教學設計所需的教材分析、學情分析、教法分析等，對課堂教學設計有很好的指導作用.

二、基于MKT理論的初中數學教學的價值

基于MKT理論的數學教學設計對于當前在學科核心素養培養的背景下

的初中數學教學來說，有比較重要的意義.一是有助于教師厘清教材思路，有效把握教學內容.教師通過對所教授內容進行MKT理論的CCK、HCK、KCC的成分分析，分別從單純的數學知識、內容與相關知識點的聯系、內容與課程的聯系這三方面考慮，弄清有關知識在教材體系中的編排，理解這樣編排的原因，認真去揣摩和欣賞，從而整體把握教材，在課堂教學中分階段落實.二是有助于學生對知識的深度理解，符合學生的認知規律.

三、對教學內容的MKT成分分析

筆者以“平面直角坐標系”這部分內容為例，對教學內容進行MKT成分分析，從而探索教學設計的新路徑.

1.一般內容知識（CCK）

CCK是指初中階段對學生普遍要求的數學知識和技能，它是一種“純”的數學知識.《上海市初中數學學科教學基本要求》對本節內容的具體要求：懂得平面直角坐標系的概念和構成;懂得平面直角坐標系內點的坐標;懂得點與坐標之間的一一對應關系.

根據成分分析，筆者在教學設計中安排了如下練習作為概念應用：

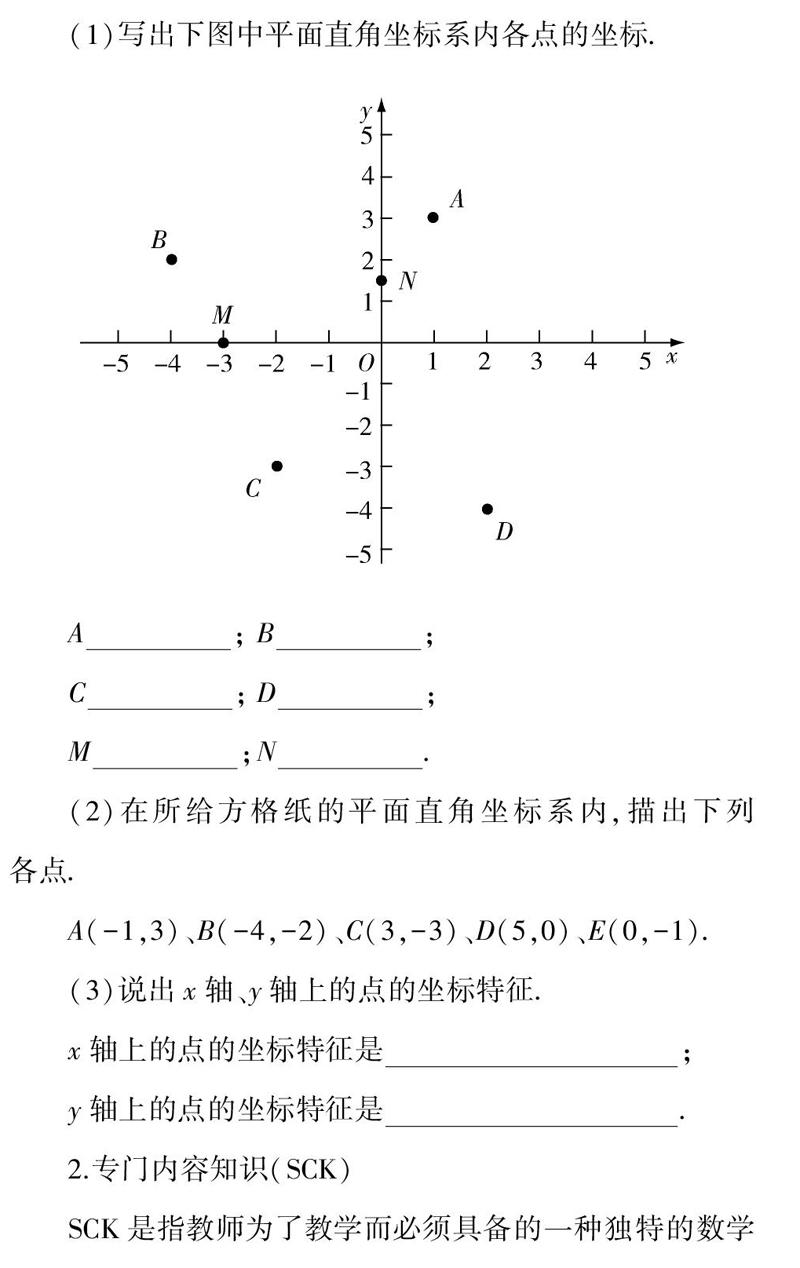
（1）寫出下圖中平面直角坐標系內各點的坐標.

（2）在所給方格紙的

平面

直角坐標系內，描出下列各點.

A（-1，3）、B（-4，-2）、C（3，-3）、D（5，0）、E（0，-1）.

（3）說出x軸、y軸上的點的坐標特征.

x軸上的點的坐標特征是????????? ;

y軸上的點的坐標特征是????????? .

2.專門內容知識（SCK）

SCK是指教師為了教學而必須具備的一種獨特的數學知識，教師有了它才能準確地表達數學概念.如數學知識、方法和思想的發生、發展和形成過程等知識.教師對教學內容進行SCK分析，厘清平面直角坐標系這一知識的發展形成過程，使學生在課堂上沿著數學家的足跡探索新知，發展數學思維，關注數學學科本質.

平面直角坐標系的發展的經歷了三個階段：單軸的確定，負坐標的出現，坐標系的出現.教師借鑒平面直角坐標系發展的歷史設計問題串，引發認知沖突，從而引入情境，讓學生探究如何表達平面上的點的位置，激發學生的學習動機，促進學生對平面直角坐標系概念建構的深入理解.具體引入環節設計如下：

有一天，笛卡爾生病臥床，但他頭腦一直沒有休息，在反復思考一個問題：通過什么樣的辦法才能把“點”和“數”聯系起來，突然，他看見屋頂角上的一只蜘蛛，在天花板上爬，蜘蛛在天花板上一會兒上下拉絲，一會兒左右拉絲.蜘蛛的“表演”使笛卡爾的思路豁然開朗.請你想一想，笛卡爾是如何表示蜘蛛在天花板上的位置的呢？

（1）如果這只蜘蛛向左爬了4米，我們可以怎么用數來表示它的位置？如果向右爬了3米呢？

（2）如果這只蜘蛛向左爬了4米，又向上爬了3米，我們可以怎么用數來表示它的位置？

3.數學水準知識（HCK）

HCK既包括關于不同的數學專題在課程中有著怎樣的聯系的知識，也包括關于某一數學專題與后面出現的概念間的聯系的知識.平面直角坐標系的知識需要結合數軸、數軸上的點與實數一一對應、相交線與平行線的相關知識.平面直角坐標系的學習是學生今后學習函數圖像和平面解析幾何的必要基礎.

根據上述分析，教師在教學設計中建立模型時，從數軸上的點與實數一一對應這個知識點引導學生構造兩條數軸，使得平面上的點與有序實數對一一對應，從一維過渡到二維.這樣的教學方式符合學生的認知規律，使學生易于理解模型的建立.

4.內容與學生的知識（KCS）

KCS指學生對教學內容的思考方式.教師應分析本節課中學生可能存在的困惑：一是對平面直角坐標系價值、作用的認識模糊，不知道為什么要引入這一概念;二是對平面直角坐標系的概念停留在記憶層面，不理解它的本質.存在上述現象是因為課堂教學脫離了數學背景，教師缺乏對數學背景的了解，不關注思維發展規律，這樣去情境化的數學教學不利于學生對數學學科本質的理解.

5.內容與教學的知識（KCT）

KCT綜合了內容和教學兩個方面的知識.具體指教師為了達成教學目標，依據學情分析、教學內容選擇有效的呈現手段設計教學過程.

筆者認為體驗、揭示知識的發生、發展過程，突破知識生成的瓶頸，合理有序地構建認識體系是本節課關鍵.本節課設計的基本流程：

由此設計五個環節：（1）創設情境，啟發思考;（2）建立模型，建構概念;（3）學習歷史，理解概念;（4）應用概念，正確辨析;（5）課堂小結，促進提升.

6.內容與課程的知識（KCC）

KCC是指關于課程的知識，這類知識陳述教學框架和課程從預設到實施再到達成的轉化過程.

四、基于MKT理論的教學設計實踐的思考

對教學內容進行MKT成分分析，這些成分從學科內容知識和教師具備的教學知識兩大方面全面涵蓋了教學設計的前期分析，分析的對象涉及學生、教材、教師.在實踐的過程中，筆者獲得了如下的思考.

1.教學嘗試新路徑：從內蘊于學科背后的認識視角出發.數學知識的產生是一個推陳出新的過程.在教學設計中，教師如果能從知識的形成和發展角度進行分析，通過歷史上知識形成過程中產生的認知沖突來預測學生在學習時的困難，就可以更好地找準難點.

2.教育現代化新要求：提升自身的專門內容知識.專門內容知識（SCK）是教師從事教學任務所需要的數學知識.教師擁有SCK才能準確表達數學概念、解釋數學法則等.教師在教學時要引導學生從數學學科的視角看世界，這就要求教師有豐富的數學學科知識，SCK能使教師著眼于數學學科的整體結構.

【參考文獻】

[1]徐章韜.面向教學的數學知識——基于數學發生發展的視角[M].北京：科學出版社，2013.

[2]徐章韜，顧泠沅.面向教學的數學知識[J].教育發展研究，2011（6）：53-57.

[3]龐雅麗.美國MKT研究的緣起、發展及啟示[J].外國中小學教育，2013（6）：36-40.