在比較中探索算理 在實踐中深化算法

屠明杰

摘要：“除數(shù)是一位數(shù)的筆算除法”是多位數(shù)除法的基礎(chǔ)，在日常生活中有廣泛的應(yīng)用。筆算除法與筆算加、減、乘法有很大的差異。算理是計算過程中的道理，解決“為什么這樣算”的問題，算法是計算的方法，解決“怎樣算”的問題。如何在多種方法的比較溝通中，幫助學(xué)生深入理解筆算除法的算理，掌握筆算除法的算法，筆者對本課進(jìn)行了實踐和思考。

關(guān)鍵詞：筆算除法;算理;算法;小學(xué)數(shù)學(xué)

“筆算除法”是人教版小學(xué)數(shù)學(xué)三年級下冊第二單元《除數(shù)是一位數(shù)的除法》的內(nèi)容。本單元主要包括口算除法、筆算除法和用估算解決問題三部分，其中“筆算除法”是本單元的教學(xué)重點。本課是在學(xué)生已經(jīng)掌握表內(nèi)乘法，能正確地口算100以內(nèi)加、減法及有余數(shù)除法的口算基礎(chǔ)上進(jìn)行學(xué)習(xí)的。它既是表內(nèi)乘法及口算除法的進(jìn)一步發(fā)展，又是進(jìn)一步學(xué)習(xí)除數(shù)是兩位數(shù)、多位數(shù)除法的重要基礎(chǔ)，起著承上啟下的作用。本課的教學(xué)目標(biāo)為：讓學(xué)生經(jīng)歷一位數(shù)除多位數(shù)筆算的探索過程，掌握一般的筆算方法，能正確地計算一位數(shù)除多位數(shù)，并能用乘法驗算。使學(xué)生能夠積極參與探索算法和解決問題的活動，同時培養(yǎng)學(xué)生認(rèn)真計算、書寫工整的習(xí)慣。

一、嘗試解答，參與探究

學(xué)生的學(xué)習(xí)過程是一個認(rèn)知的過程，也是一個探索的過程。有效的數(shù)學(xué)活動是學(xué)生學(xué)和教師教的統(tǒng)一，學(xué)生是學(xué)習(xí)的主體。本單元從一開始就用具體熟悉的情境（分書）人手，在對情境中數(shù)學(xué)信息的分析的基礎(chǔ)上引出問題，讓學(xué)生理解計算是解決問題的方法，產(chǎn)生計算的需要，從而形成學(xué)習(xí)的內(nèi)部動機(jī)。

師：這里有8本美術(shù)書要平均分給4個班，每個班可以得到幾本？

生：2本。

師：那如果是80本書平均分給4個班呢？

生：20本，因為8÷4=2，所以80÷4=20n

師：那我們在分80本書的時候是一本一本分嗎？

生：不是。我們可以十本十本分，每個班級分到2個十本。

師板書：8個十除以4是2個十，就是20。

接著讓學(xué)生分800本書。

生：一百一百地分，8個百除以4，每個班得到2個百，就是200。

接著讓學(xué)生分120本書。

生：如果要一百一百地分，只有1個百不夠分，就把120看作12個十，12個十除以4等于3個十，就是30。

學(xué)生有了分書的感受，對口算除法中為什么可以先不看被除數(shù)后面的0有所感受，從而在探究過程中逐漸理清事物的本質(zhì)。然后，學(xué)生展示自己的想法，全班交流，使他們在民主寬松的情境下自我檢查反思，逐步體驗成功，增強(qiáng)自信心。

二、比較聯(lián)系，理解算理

本單元的計算教學(xué)多是在學(xué)生原有的知識基礎(chǔ)上進(jìn)行的，數(shù)學(xué)知識在內(nèi)容上包含了深刻的思維和豐富的知識，在學(xué)習(xí)過程中學(xué)生會出現(xiàn)思維斷層。因此要找準(zhǔn)新舊知識之間的聯(lián)系，多采用對比的方式促進(jìn)知識的遷移類推，促進(jìn)學(xué)生的有效發(fā)展。在講授筆算除法第一個例題時，繼續(xù)沿用分書的情境：42本書平均分給2個班，每個班可以分到幾本？讓學(xué)生先獨立思考，并用自己的方法把答案算出來。課堂展示的四種方法是逐漸遞進(jìn)、不斷上升的。

（一）對比：方法一與方法三

師：看看它們之間有什么聯(lián)系和相同的地方？

（師指方法一中的“21”，是怎么算出來的）

生：二二得四，一二得二，我能想到2乘21會得到42。

師：方法三里下面一個42怎么得來的？

生：2×21。

師：它們都表示什么意思？

生：2個21。

（二）對比：方法二與方法四

這兩種方法是新舊知識之間的跨越，從橫式出發(fā)引導(dǎo)學(xué)生尋求豎式中的對應(yīng)數(shù)位。學(xué)生質(zhì)疑“20在除法豎式中的哪兒？”使得溝通不再停留于表面，而是將溝通融人一個整體，“2在十位上，表示2個十”體現(xiàn)的是豎式中位值制的原則，“2個十乘2就是4個十，所以是40，在對應(yīng)的數(shù)位下面寫好4，表示分掉4個十。”可見口算與豎式算理是一樣的，只是形式不同。這樣指引學(xué)生感悟橫豎式之間的內(nèi)在聯(lián)系，將其延伸至思維深處。

（三）對比：方法三與方法四

師：仔細(xì)觀察，比一比這兩個豎式一樣嗎？哪里不一樣？

生：少了一層樓。

師：為什么方法四還要多蓋一層樓呢？

生：方法四體現(xiàn)了分的過程，方法三其實是直接想到了答案寫在上面，和口算沒什么區(qū)別。

師：我們能不能把方法四直接簡寫成方法三的形式？

生：不可以，如果遇到復(fù)雜的，不能直接想出答案，就不能一層樓解決了。

師：是的，在我們以后學(xué)到被除數(shù)、除數(shù)的位數(shù)更多的除法時，會更加體會到這一點，需要我們一步步除，一步步分，最后求出答案。

師：像這樣用豎式計算的除法，就是我們今天要學(xué)習(xí)的筆算除法。（揭題）

這兩種豎式方法，學(xué)生很清楚地發(fā)現(xiàn)少了一層樓的步驟，那么關(guān)鍵問題“下面一層能省去嗎？”揭示了問題的本質(zhì)，這是除法算理的體現(xiàn)，適用于每一道筆算除法的通用的規(guī)范格式。

相對于加法、減法和乘法，筆算除法總顯得比較另類，前者的筆算都是從個位算起，而除法卻要從高位算起。這是對學(xué)生先前學(xué)習(xí)經(jīng)驗的挑戰(zhàn)，這個教學(xué)過程中不僅要讓學(xué)生掌握筆算除法的過程、理解每個步驟的算理，還要體會到規(guī)范豎式的優(yōu)勢。

三、循理入法，明確算法

（一）強(qiáng)化算法，規(guī)范語言

教師帶領(lǐng)學(xué)生規(guī)范書寫，規(guī)范的書寫格式可以表達(dá)學(xué)生的運算思路和計算方法、步驟，防止錯寫漏寫數(shù)字和運算符號，同時引導(dǎo)學(xué)生完整敘述筆算過程。先讓幾個語言表達(dá)能力強(qiáng)、思維敏捷的學(xué)生說，接著同桌相互說，這樣多次敘述算法，避免了豎式計算開始就出錯的現(xiàn)象，很好地強(qiáng)化了算法。

（二）知識遷移，類推算法

在完成兩位數(shù)除以一位數(shù)的基礎(chǔ)上，出示三位數(shù)除以一位數(shù)的筆算，讓學(xué)生獨立嘗試解決。這樣在原有兩位數(shù)除以一位數(shù)除法的基礎(chǔ)上，推動新知識的學(xué)習(xí)，不僅可以取得事半功倍的教學(xué)效果，還能調(diào)動學(xué)生學(xué)習(xí)的積極性，讓他們學(xué)會如何探究，形成遷移類推的思想和方法。

（三）歸納提升，形成模型

組織學(xué)生回顧用豎式計算的步驟、方法，討論交流“筆算除法要怎么算？”。學(xué)生發(fā)現(xiàn)在除任意一位的時候，都要經(jīng)歷“除、乘、減”這三步，并且完成這三步以后要把被除數(shù)的下一個數(shù)“落”下來，繼續(xù)除。學(xué)生整理出了“除、乘、減、落”這樣的步驟以后，每算一層都按這樣的順序重復(fù)去做，思路就比較清晰了。教材并未給出文本法則，意味著教學(xué)時無須學(xué)生機(jī)械記憶，而要把重點放在引導(dǎo)學(xué)生基于個體經(jīng)驗進(jìn)行適當(dāng)?shù)臍w納總結(jié)，使得原有的計算經(jīng)驗更加清晰。

四、強(qiáng)化練習(xí)，提高質(zhì)量

教師要遵循學(xué)生的認(rèn)知規(guī)律，適當(dāng)?shù)剡\用基本練習(xí)、改錯練習(xí)、綜合練習(xí)等，滿足各層次學(xué)生的需要，使每個層次的學(xué)生都有事可做。

（一）抓住易錯知識，突出針對性

針對學(xué)生易錯的或者預(yù)測學(xué)生可能會錯的的題設(shè)計針對性練習(xí)，幫助學(xué)生真正掌握算法。在小結(jié)注意點時，提醒學(xué)生如果有余數(shù)要余著繼續(xù)算，如果不能整除，要想最大能商幾，這樣才能保證余數(shù)要比除數(shù)小，每一步要算清楚算完整。通過這樣針對性的練習(xí)，幫助學(xué)生掌握“筆算除法”的算法，避免學(xué)生在算法上出現(xiàn)的錯誤，使教學(xué)獲得較好的效果。

（二）訓(xùn)練計算速度，關(guān)注開放性

在基本練習(xí)的基礎(chǔ)上，設(shè)計答案不唯一的開放題，學(xué)生自主探索不同的除法豎式，有利于開拓學(xué)生思路，展開發(fā)散思維，培養(yǎng)學(xué)生的創(chuàng)新意識。同時也有利于訓(xùn)練計算的速度，比比看，誰編得又多又對。

（三）加強(qiáng)理法聯(lián)系，重視應(yīng)用性

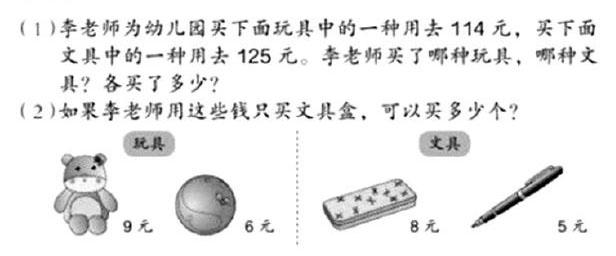
這道題需要綜合運用一位數(shù)的乘、除法知識，第（1）小題學(xué)生一般會用逐一嘗試的方法，由能否正好除盡得到整數(shù)商來判斷。教師可引導(dǎo)學(xué)有余力的學(xué)生觀察題目中數(shù)據(jù)的特點，應(yīng)用基本的乘、除法口算做出判斷。例如，根據(jù)125的個位數(shù)是5，判斷出文具的單價不可能是8元，然后通過筆算進(jìn)行驗證。讓學(xué)生體會這種先通過口算或估算找到解題思路，最后用筆算來驗證的解題方法，提高學(xué)生解決問題的能力。

算理為計算提供正確的思維方式，保證計算的合理性和正確性，算法為計算提供快捷的操作方法，提高計算的速度。算理往往是隱性的，算法往往是顯性的，它們相輔相成，算理的探析有助于學(xué)生探索算法、掌握算法。在小學(xué)數(shù)學(xué)課程中，計算教學(xué)占據(jù)著較大的比重。新課程視野下的計算教學(xué)雖然在具體的要求與處理上有了一些實質(zhì)性的變化，但只要把握好“算理”和“算法”這兩條主線，努力踐行新課程的教學(xué)理念，就會達(dá)到筆算除法教學(xué)的理想狀態(tài)。