數形結合思想在高中數學解題中的有效滲透

伊斯馬依力·吾吉艾麥提

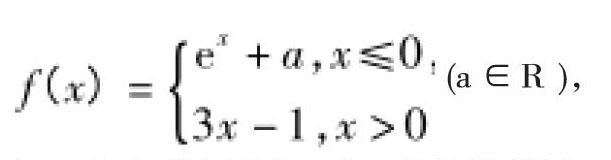
摘要：在高中數學教學中，數學知識的學習與解題技巧受到越來越多人們的關注，為了構建高效課堂、促進教學實踐活動的順利開展，許多老師開始重新調整教學策略和教學方向，既堅持學生的主體地位，又十分關注教學策略和教學手段的穩定革新，在引導和鼓勵學生的基礎上豐富課堂教學內容和形式，保證學生在一個自由寬松的學習氛圍下實現個人的良性成長和發展。

關鍵詞：數形結合;高中數學教學;解題應用

引言

高中數學在很大程度上決定著高考成績的高低，高中數學知識的學習對于很多同學來說存在一定的困難，因為需要對大量的數學概念進行記憶和應用，而數形結合的滲透，會幫助大家更好地掌握基礎知識，為同學們高考成績的提升提供保障。下面就來探討數學學習中如何使用數形結合思想。

1數形結合思想方法

數與形是高中數學教學的重點和難點，老師需要了解不同的數量關系和空間圖形分析要求之間的內在邏輯聯系，結合學生的學習能力和學習背景，積極闡述數量關系與圖形之間的轉化關系。其中空間圖形能夠轉變為數量關系，數量關系也可以直接轉變為不同的空間圖形，兩者的聯系和互動非常頻繁。要想保證學生掌握高中數學學習的核心，老師必須要關注數與形之間的融合和轉化，有效應用數形結合思想彌補學生在想象力和邏輯思維判斷力上的不足，營造一個更加生動直觀的學習氛圍，讓學生在自主學習的過程中，主動利用所學知識解決生活實際中的相關問題，將抽象困難的問題轉化為簡易的題目，通過不斷的自主分析和獨立思考提高學習積極性，產生源源不斷的學習動力。

2數形結合思想方法在高中數學教學中的應用

2.1數形結合，簡化習題結構

在高中數學中，“數”與“形”是學生在三年學習中的主要研究對象，只要找準二者之間在固定情境下的對應關系，就可以對二者進行任意轉換。在高中數學解題過程中，數形結合這一數學思想的應用可以幫助學生簡化實體條件。在很多情況下，原本很復雜、很抽象的題設條件用圖像的形式表現出來，一下子就變得一目了然了，在這種前提條件下，以形助數可以幫助學生節省很大一部分的題目解析時間，提高學生的解題效率，而且，借助圖像來輔助解題，有助于學生對數學概念的深層次理解。因此，在日常教學，教師就應該有意識地鍛煉學生借助圖形來分析題目的能力，讓學生在短時間內抓住題干條件的重點，把題目中的隱含信息清晰地在圖形上表現出來，借助圖形去輔助簡化遇到的問題。同時，教師在日常授課過程中，要著重注意對一些數學規律以及數學定理的證明，能用圖形進行輔助證明時一定不要放過這次機會，讓學生在一點一滴的積累中內化數形結合的思想。

2.2在方程問題中采用數形結合思想方法

方程問題是高中數學的核心模塊之一。這一模塊對學生的邏輯思維能力要求更高，老師可以著眼于數形結合思想方法，通過繪制數軸的形式，讓學生對不同的方程有一個客觀的認知。數形結合思想方法能夠確定坐標軸之中拋物線的開口方向和焦點，學生可以在老師的引導下，在圖形紙上畫出不同的方程式，然后結合個人的社會生活實踐經驗和所學習的數學知識進行分析和遷移。這種教學策略能夠加深學生的認知和理解，幫助學生梳理知識脈絡和框架，從整體上提高學生的學習能力。

2.3利用數形結合解集合問題

在解答集合問題時，學生要完成答題需要一定的空間構思能力，也會有一定的難度。在集合問題中應用數形結合思想，可以讓問題變得更加直觀，提高學生解題效率，降低錯誤率。集合問題在運用數形結合的方法時，一般把圓視作一個集合，通過兩圓相交、兩圓相離的情況，可以直觀地看出集合之間有沒有公共的數集，對集合之間的關系可以有準確的把握。用畫圖的形式可以降低演算量，把計算簡單化。在解不等式的取值范圍問題時，可以利用畫數軸圖形的方式來解決問題，讓問題變得簡單。

2.4嚴謹清晰推理、強化解題能力

教師在數學解題中滲透數形結合思想，要注重對學生探究、批判、反思能力的綜合培養，讓學生在解題過程中能對數學語言進行細致入微的觀察，通過周到、全面的自主構圖進行嚴謹準確的分析思考，借助數形結合思想得出準確結論. 因此，為了進一步強化學生數形結合解題思想，教師可以組織學生運用常規解題思路，對比數形結合進行思考，讓學生在對比、觀察、歸納的分析中，能深刻感受到數形結合的價值優勢，從而有效提高學生的解題意識和解題能力.

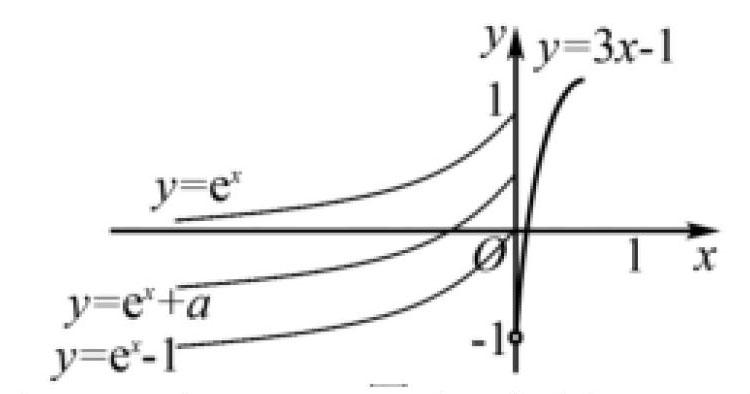
例如，已知函數（a∈R），若f（x）在 R 上有兩個零點，求 a 的取值范圍. 在學生進行推理和構圖的過程中，教師要遵循循序漸進的教學原則，讓學生利用圖形來揭示數學知識概念，通過感性到理性的認知，巧妙運用數形結合加深對數學知識的掌握理解. 如圖所示：

當 x >0 時，f（x） =3x -1 有一個零點 x =1/3，因此，當x≤0，f（x） = e x + a =0 只有一實根。結合圖形可知- 1≤a<0. 促使學生在解題過程中交叉靈活地融合抽象與形象思維，提高自身數學解題能力。

結語

綜上所述，教師在數學課堂中滲透數形結合思想，要注重對學生發散性思維和直觀思維的綜合培養，引導學生在解題過程中靈活運用多向思維對問題進行分析、推理、聯想，促使學生可以從整體角度，對數學問題結構本質進行識別判斷，提高解決問題的效率和靈活性。同時，教師要為學生提供充足的思考空間，讓學生在自主探索、討論交流解題過程中，大跨度地遷移思路和方法，通過數與形的巧妙結合，創造性地解決問題。

參考文獻

[1]王小峰.探析高中數學教學過程中常用的思想方法[J].數學學習與研究，2018，（9）：41.

[2]蘇心怡.數形結合思想在高中數學解題中的應用淺析[J].考試周刊，2019（15）：104.

[3]李曉明.高中數學教學與解題中數形結合思想方法的應用分析[J].中國新通信，2018，20（07）：209.