變式訓練突破中考壓軸題

廣東省恩平市年樂夫人學校

1 原題呈現(xiàn)

題目如圖,拋物線y=ax2+bx+x與x軸的交點為A(-6,0),與y軸的交點為C(0,3),且經(jīng)過點G(-2,3).

(1)求拋物線的表達式;

(2)點P是線段OA上一動點,過點P作平行于y軸的直線與AC交于點Q,設ΔCPQ的面積為S,求S的最大值;

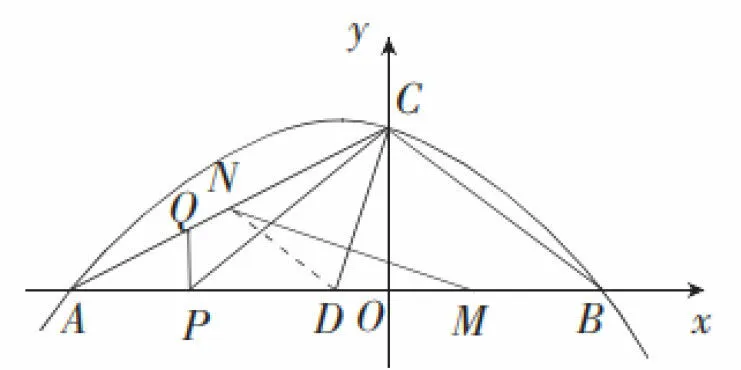
圖1

(3)若點B是拋物線與x軸的另一交點,點D、M在線段AB上,點N在線段AC上,∠DCB=∠CDB,CD是MN的垂直平分線,求點M的坐標.

2 題目分析

本題考查的知識主要有,待定系數(shù)法求函數(shù)解析式、二次函數(shù)的基本性質(zhì)和綜合應用,三角形中位線、等腰三角形的性質(zhì)、線段垂直平分線的性質(zhì)、平行線的判定和性質(zhì)等知識點.在(2)中設出P點坐標,用代數(shù)式表示出PQ的長,然后引導學生求ΔCPQ的面積,實際上就是求S梯形QP OC與SΔP OC的差.同時注意函數(shù)性質(zhì)的應用.在(3)中推算出DM=DN=12BC是解題的突破口.

3 題目解答

(1)把A、C、G三點坐標代入拋物線解析式,可得

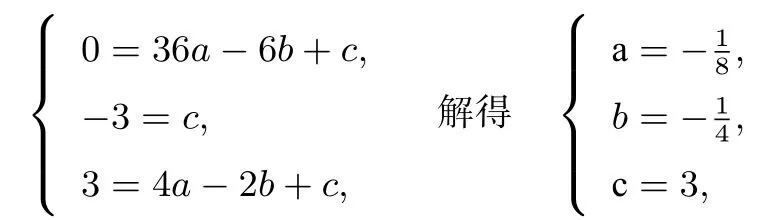
點評本題考查知識點較多,綜合性質(zhì)很強.在解題時,先利用待定系數(shù)法,把A、C、G三點坐標代入可求得拋物線解析式.

(2)因為C(0,3),所以,可設直線AC解析式為y=kx+3.把A點坐標代入,可得0=-6k+3,解得所以直線AC解析式為

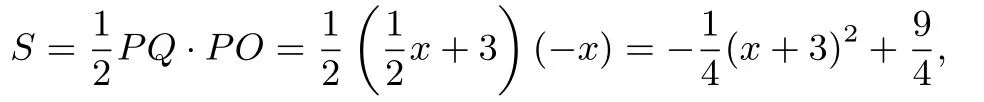
點評在(2)中設出P點坐標,用代數(shù)式表示出PQ的長,然后引導學生求ΔCPQ的面積,實際上就是求S梯形QP OC 與SΔPOC的差.再結合二次函數(shù)的性質(zhì)可求得S的最大值.

點評第(3)問由條件可求得可求得點D為AB的中點及坐標有∠DCB = ∠CDB和CD是MN的垂直平分線,可證明DN//BC 得出DN為ΔABC的中位線,所以從而得點M的坐標.

4 變式訓練

變式訓練1在(2)的條件下,延長直線PQ 交拋物線于點M,線段MQ 會不會存在最大值,若存在,請把它求出來;若不存在,請說明理……