幾何中角度最值問題的另法探析

廣東省深圳市華強職業技術學校

廣東省惠州市博羅中學(516100)易 敏

1 常見的角度最值問題

例1點A 與點B的坐標分別是(1,0),(5,0),點P是在該直角坐標系內的一個動點.當點P 在y軸上移動時,∠APB是否有最大值？若有,求點P的坐標,并說明此時∠APB最大的理由;若沒有,也請說明理由.

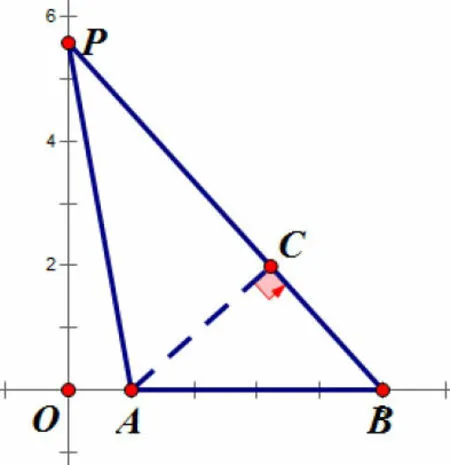
圖1

如圖1,過點A作AC⊥ PB,垂足為C,設P(0,y),則OP = y,因為∠CBA = ∠OBP,∠BCA = ∠BOP,所以ΔBCA ∽ΔBOP,所以在RtΔACP中,

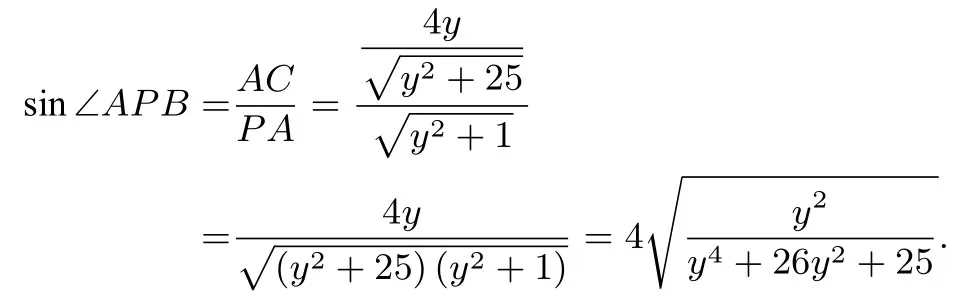
該題是中學常見的角度最值問題,我們可以發現幾何中角度的最值問題往往不是直接用角度進行描述的,通常要利用三角函數進行轉化.通過三角函數的解析式分析,求出三角函數的最值,再利用角度與三角函數的關系,從而達到求解角度最值的目的,這種方法我們稱為三角函數解析法.三角函數解析法的優點是方向很明確,分析所求角的三角函數解析式的最值,利用三角函數的單調性,從而分析出角的最值.但其難點和關鍵就在于三角函數解析式的求解和分析,當三角函數解析式較為復雜時,就難以判斷三角函數的最值了.

另法探析既然三角函數解析式的求解和分析是一個難點,那么我們是否可以繞開求解三角函數解析式？那角度的描述還有什么途徑呢？在平面幾何中,我們還學習過相關角.只要我們找到相關角以及確定的相關關系,那么求解相關角的最值,進而就能夠分析出所求角的最值了.問題的關鍵就轉化為求解相關角了,而不用三角函數解析法又如何描述相關角的最值呢？下面我們先了解兩個結論……