例談幾何題的命制方法

江蘇省泰州市第二中學附屬初中

命制試題的方法之一就是命題者從原有試題得到啟發,對原有試題進行深度的改造,再加工,使之形式上有所改變、在原有考查知識點上進行拓展變化而編制成的創新題.由于是對原有試題的深挖掘,所以命制的試題一般都帶有一定的新穎性和創造性.創新的方法很多,例如:改變設問角度、改變已知條件、改變考查目標、轉換題型、題目重組等,一道好的創新題應當是既考查知識和能力又滲透數學思想,其核心是能夠培養學生的核心素養.源自經典,傳承創新是試題命制的常用途徑.下面筆者從一道經典的幾何問題出發,通過對近年來中考中出現的有關試題的分析,來了解其命題思路,感悟幾何題的命制方法.

1 典型例題

如圖1,正方形ABCD中,以A為頂點作∠EAF=45°,其兩邊分別交BC,DC于點E,F.求證:EF=BE+DF.

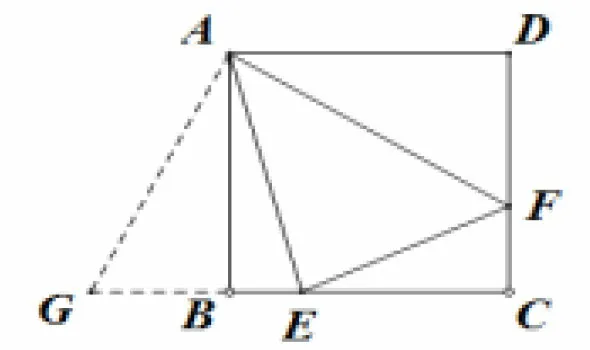
圖1

分析:只要將ΔADF繞A點順時針旋轉90°,或用“補短”法在CB的延長線上取BG=DF即可.

1.1 引申結論

解題的過 程中,我 們 得 到 ΔABG∽= ΔADF,ΔAEG∽= ΔAEF.于是有

下面以此題為例,介紹幾種常用的命制方法.

2 互換因果

把原題中的∠EAF= 45°與結論“EF=BE+DF”或結論1○之一,或2○,或3○,或4○互換得到五個新的命題.可以證明它們都是成立的.即上述六個性質中,只要其中一個成立,其余五個都成立.

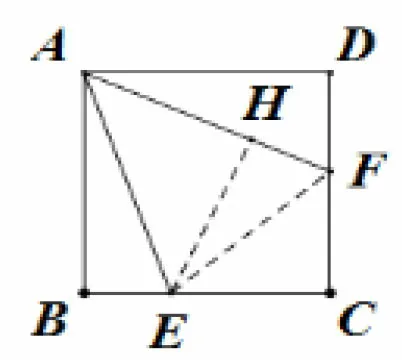
圖2

例1如圖2,正方形ABCD中,E為BC上一點,BE=為CD的中點.求證:∠EAF=45°.

思路(1)連結EF,設正方形邊長為1,由勾股定理算得EF=再運用原題的分析中的方法.

思路(2)再作EH⊥AF,H為垂足,先算出EF,AF和AE的長,分別為再算出AH的長度.由可得.AH的長可通過如下方法得到……