激活思維,方得奧妙—-一堂向量典型問題習題課設計

安徽省安慶市懷寧縣新安中學

1 創設情境,引入問題

教師:同學們,之前我們學習了平面向量基本定理,平面向量基本定理告訴我們,平面內任意一個向量都可以用兩個不共線的向量量化,這為我們研究問題帶來極大的方便.同時,平面向量基本定理也是整個向量理論的基礎,所以我們一定要學好這個基礎,為后面的學習做好準備,今天我們繼續學習有關平面向量基本定理的一些應用.

例1如圖1,平面內有三個向量其中與的夾角為120°,的夾角為30°,且若則λ+μ的值為___

圖1

圖2

教師:大家回顧平面向量基本定理的推導過程,中間作了一條什么樣的輔助線? 你能用類似的方法解決這道題嗎?

學生1:如圖2,過終點C作其中一個基底的平行線交另一個基底OA于點D,則于是λ=4,μ=2,λ+μ=6.

教師:很好,這位同學用了作基底平行線的方法得出了正確答案,而且計算量也不大.請大家積極思考,還有其它的方法嗎?

學生3:我用的是建立坐標系的方法,以O為坐標原點,OA為x軸建立平面直角坐標系,寫出向量的坐標,代入得到兩個關于λ,μ的兩個方程,從而解出λ,μ.

教師:非常棒.這道題現在我們有3 種解法,但在實際運用時大家還要注意選擇合適的方法.

練習選擇合適的方法解答下面這道題:向量a,b,c在正方形網格中的位置如圖3所示,若c=λa+μb(λ,μ ∈R),則

圖3

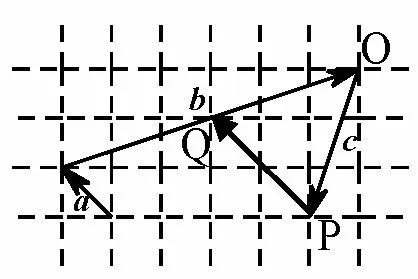
圖4

圖5

教師:讓學生思考題中的向量a,b,c是如何給出的? 結合網格的特點,選擇適當的方法.

學生4:我用的作基底的平行線法,因為在網格中可以很方便的看出長……