解析基本圖形 樹立模型意識—-一道三角形全等問題的教學反思

廣東省東莞市常平中學初中部

基本圖形一般是指在教材中描述圖形定義、公理、定理的圖形,以及一些具有代表性的例題和習題中的圖形.解析基本圖形,能夠幫助學生快速找到幾何綜合題的解題突破口,攻破教學難點,提升解題效率,發展學生的幾何直觀和邏輯推理能力.

1 提出問題

1.1 題目呈現

問題1如圖1,正方形ABCD中,E是對角線BD上一點,連接CE,過點E作EF⊥CE交AB于點F,求證:EF =EC.

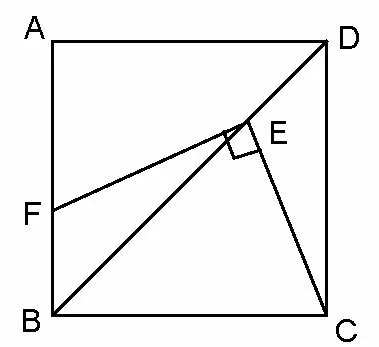
圖1

這是八年級下冊《平行四邊形》期末復習中的一道練習題,在規定時間里全班48名學生僅有3人成功解答.其實本題的證明過程不算復雜,只要學生對正方形的軸對稱性有一定的感知,對此前學習正方形的性質時解決過的一些基本圖形有所印象,比較容易想到的是添加一條輔助線構造一對軸對稱的全等基本圖形的解題思路,如圖2,圖3.

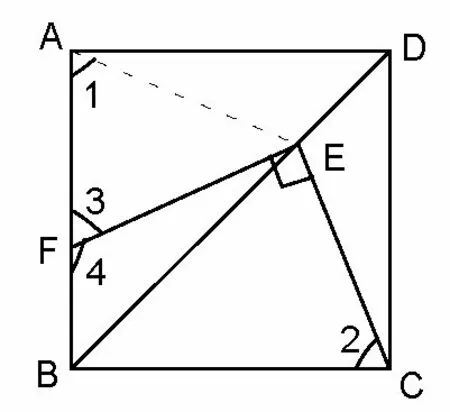
圖2

圖3

以圖2為例,連接AE,易證ΔABE∽= ΔCBE(或ΔDEA∽= ΔDEC),得到EA=EC,∠1=∠2,然后由四邊形EFBC內角和得出∠4+∠3 = 180°,再轉化出∠1 = ∠3,進而EA=EF,最后等量代換證得EF=EC.

1.2 障礙分析

通過交流發現,最初多數學生陷入了證明“ΔBFE∽= ΔDEC”的誤區,找不齊全等的條件,一部分學生想到了添加輔助線,嘗試“連接FC,然后努力證等角對等邊”,朝這兩個方向努力的學生都感到條件“EF⊥EC”難以利用.說明學生對這類需要添加輔助線構造全等三角形的問題缺乏解題經驗,對題目中隱含的基本圖形(如圖4,圖5)表征的識別存在較大困難,無法利用過往經驗,造成解題效率低下.

圖4

圖5

2 利用基本圖形分析法的解題教學

解析基本圖形是中考壓軸幾何綜……