培養學生幾何直觀能力的策略

陳炎秀

摘 要：幾何直觀主要指利用圖形描述和分析問題。《全日制義務教育數學課程標準（2011年版）》（以下簡稱《數學課程標準》）將“幾何直觀”正式列為十個核心概念之一。通過幾何直觀能夠把抽象、深奧的數學知識變得具體、直觀，簡單明了，學生容易理解掌握，同時可以發展學生的空間思維觀念。文章從幾何直觀的教學價值以及培養學生幾何直觀能力的教學方法這兩個方面進行闡述、論證。

關鍵詞：幾何直觀;直觀感知;數形結合

中圖分類號：G623.56 文獻標識碼：A 收稿日期：2019-01-10 文章編號：1674-120X（2019）10-0073-02

一、幾何直觀的教學價值

《數學課程標準》首次指出在義務教育階段應當重視培養學生的幾何直觀能力，將“幾何直觀”正式列為十個核心概念之一。這凸顯了幾何直觀在學生數學學習過程中的地位和作用，彰顯了幾何直觀的教學價值。

二、培養學生幾何直觀能力的教學方法

（一）模型表征，建立表象

幾何直觀的形式主要有兩大類：一類是規范的直觀模型，如數尺、數軸、小方塊等，一類是個性化的示意圖。直觀模型在學生學習數學的過程中起非常大的作用，可以讓學生直接接觸到數學的本質。根據教學任務，教師要靈活地選擇所需的教學材料，在教學中根據實際情況合理地利用直觀模型，幫助學生從直觀模型中觀察、探索出更多數學信息。培養學生空間觀念離不開觀察與想象。通過全面、有序的觀察活動，學生對所觀察的物體有了整體的認識，會在頭腦中形成表象。

在幾何教學中，教師準備多個直觀模型，可以讓學生看、摸、玩、拼、畫， 讓學生親歷過程。學生通過觀察感知，能夠了解幾何圖形的特點，為今后的學習奠定基礎。這樣既發展了學生的觀察能力，也提升了學生的空間觀念。

如我對人教版四年級下冊《觀察物體》進行的教學設計：

師：請同學們仔細觀察屏幕上的圖形，三個小朋友站在不同的方位觀察，請說出他們是站在哪里觀察的。

生：文文站在上面看的，紅紅站在正面看的，明明站在左面看。

師：是不是這樣呢？請同學們拿出自己帶來的小正方體，和同桌一起搭一搭，從不同方位看一看，驗證跟他們看到的是否一樣。

教材首先出示直觀模型，引發學生想象;其次是學生通過實際觀察親手搭的立體圖形，驗證自己所搭的立體圖形與看到的是不是相同，形成圖形的表征，發展空間觀念。

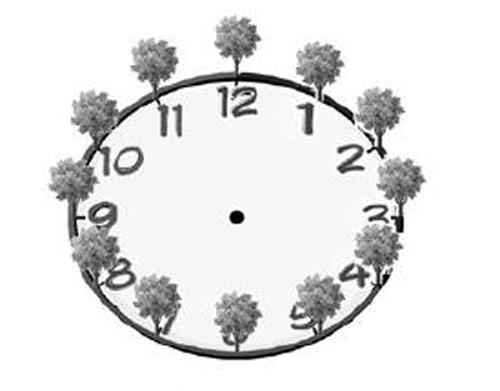
又如我在教學人教版五年級《植樹問題》這一課時，通過時鐘花圃圖片這一個性化的示意圖，把4種植樹情況串成一個情境：工人叔叔要在這個花圃植樹，每個數字邊種一棵數，第一天從數字12種到數字4，第二天接下去種到數字8，第三天種剩下的。通過花圃圖片，學生可直觀地理解只栽一端、兩端都栽、兩端不栽和封閉圖形的4種植樹情況，以及各種植樹情況的點與間隔之間的關系。

直觀模型是培養學生幾何直觀能力的有效載體，借助直觀模型可以促進學生從幾何直觀的角度去思考、分析問題，并在不斷的成功體驗、合理運用中形成幾何直觀的能力。教師經常在課堂上使用直觀模型，能夠潛移默化地讓學生認識到它們的重要作用，積累幾何直觀的經驗。

（二）操作表征，形成直觀

小學生年齡小，他們的思維發展主要以具體形象思維為主，并且伴隨著一定的直觀動作思維，逐漸過渡到抽象思維。在進行數學教學時，教師應讓學生多動手實踐，同時通過“數、擺、畫、量、折、拼”等操作活動，將知識展示給學生，把抽象知識具體化、直觀化。這不僅能有效地提高學生的學習興趣，使學生建立正確而清晰的概念，而且有助于其直觀思維能力的發展。學生們經過自己動手操作，可提升幾何直觀能力。

如我在教學《11～20 各數的認識》時，首先拿出11 根小棒，讓學生先動腦思考，如何擺能很快看出是 11 根。然后給學生展示不同擺法： ① 一邊放 6根，另一邊放5 根; ②一邊放5 根，另一邊放 6 根; ③一邊放 10 根，另一邊放 1 根; ④一邊放 2 個 5 根，另一邊放 1 根; ⑤一邊放5 個 2 根，另一邊放 1 根……學生先觀察、討論，然后歸納出：第 ③ 種和⑤種想法是一樣的，都是先擺 10 根（ 10 根為一捆），再擺 1 根。接著擺一擺 11～ 20 各數，學生先拿出一捆，再加上幾根。通過這樣的活動，學生親身經歷數概念的產生。由于形成過程清晰明確，學生們體驗到了成功的喜悅，學習熱情高漲，注意力集中，有效地理解和掌握了知識，創新意識與實踐能力也得到了培養。

學生在動手操作的過程中，通過觀察、比較、分析、綜合，既可以發展思維能力，又能夠增強感知體驗。從這里開始，學生的幾何直觀能力逐漸萌芽，他們在操作中主動探索、豐富感知、形成表象，建立空間觀念，培養幾何直觀和推理能力。

（三）數形結合，發展直觀

我國著名的數學家華羅庚說：“形缺數時難入微，數缺形時少直觀。”“數形結合”思想是重要的數學思想。數形結合的思想方法，就要讓形象思維和抽象思維相互作用，實現圖形性質與數量關系的相互轉化，把直觀的圖形和抽象的數量關系結合起來研究數學問題，使學生了解正確畫圖、借圖分析和體驗畫圖解決問題的好處。我們用得最多的是畫線段圖，借助線段圖把復雜的數學問題直觀化，這利于學生理解問題、分析問題、解決問題，突破難點。