如何培養(yǎng)高中學生的數(shù)學直觀想象能力

賀煥華

【摘 要】 隨著新課程改革的深化和推進，主要基于學生數(shù)學核心素養(yǎng)的數(shù)學課堂改革是教師們熱議的話題。文章針對如何培養(yǎng)高中學生數(shù)學核心素養(yǎng)中的直觀想象能力進行了分析和研究。并在實際教學的過程中，對理論教學活動進行教學實踐，力求進一步促進學生對數(shù)學直觀想象能力的理解和識記運用能力的提升。

【關(guān)鍵詞】 直觀想象能力? 高中數(shù)學? 想象能力

一般來說，直觀想象主要是基于當前的幾何模型的視覺直觀加以學生的空間抽象思維能力來進行科學合理的想象，是利用學生對圖形理解和想象來解決生活中的數(shù)學問題的思路過程。近幾年來我國有關(guān)高中生直觀想象能力教學的研究相對較多，本文主要針對當前的實際教學活動探究如何培養(yǎng)高中學生的數(shù)學直觀想象能力。

一、用幾何模型培養(yǎng)學生的直觀想象能力

在數(shù)學教學的過程中，教師不但要對學生進行相關(guān)練習來對習題來進行掌握，教師除了要讓學生對相關(guān)練習題進行深入的解決，同時還要對學生的直觀想象能力進行提升。其次教師還要通過相關(guān)的組織應用來對知識進行掌握，教師還可以使用比較合適的教學活動來對學生進行培養(yǎng)和鍛煉。從而更好的讓學生的直觀想象能力進行加強，讓學生對空間位置關(guān)系以及圖形描述來對數(shù)學問題進行深入分析，為學生學習質(zhì)量的提升奠定相應的基礎。在當前的高中教材中，對于立體幾何圖形設計過程中，教材內(nèi)容和實際模型有著直接的關(guān)系。

二、用三視圖培養(yǎng)學生的直觀想象能力

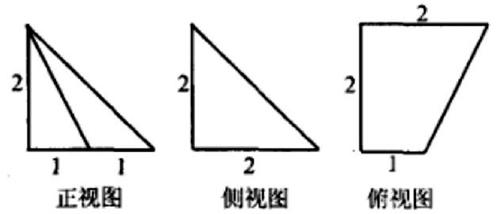
三視圖是高中階段學生學習的主要組成部分，這也是對學生直觀想象能力進行培養(yǎng)的關(guān)鍵內(nèi)容。因此，在進行這類數(shù)學題目的解決過程中，教師不能直接為學生明確答案，還要對學生加以正確引導，讓學生展開相應的想象，可以讓學生小組合作學習，自主思考后進行討論。教師還可以對學生進行輔助，幫助學生形成相應的直觀想象能力，讓學生可以在三視圖的觀察中促進學生直觀想象能力的提升。例如，當前該三視圖是一個五面體的三視圖，同時其正視圖和側(cè)視圖是等腰直角三角形，俯視是一個直角梯形，一些邊長都在圖形中進行標記，求當前五面體的實際體積是多少？

在對這個題目解答的過程中，數(shù)學教師需要對學生進行正確引導，讓學生可以將自身的直觀想象能力充分發(fā)揮。教師還可以讓學生將當前的三視圖進行相應的整合，使其形成一個相對完整的五面體。其次還可以基于當前現(xiàn)有的實際數(shù)據(jù)來進行五面體的計算，從而為學生直觀想象能力的提升奠定相應的基礎。充分利用當前的已知條件來選擇相關(guān)的三視圖，同時也是對學生直觀能力進行鍛煉的有效教學活動。因此在進行教學的過程中，需要通過相對合理的教學手段和教學方式促使學生的課堂主體性充分發(fā)揮。用最適當?shù)慕虒W活動組織形式促進教學質(zhì)量的提升和教學效率的提升。讓學生可以在提升直觀想象能力的同時，提升自身的數(shù)學基本素養(yǎng)。

三、圖形結(jié)合培養(yǎng)學生的直觀想象能力

學生的直觀想象能力主要是源于對相應的直觀感知和空間思維，要培養(yǎng)學生學會感知事物形態(tài)上的變化，利用圖形結(jié)合來對學生的直觀想象力來發(fā)展直觀想象能力。對相關(guān)數(shù)學概念進行分析和判斷，用具體的數(shù)學問題來促進學生的數(shù)學學習問題解決能力進行提升。例如，已知空間四邊形ABCD，且AB≠AC，AE是三角形ABC的邊BC的高，DF是三角形BCD的邊BC上的中線，因此求AE和DF是異面直線。這屬于一道比較簡單的習題，但是在對問題解決的過程中，相關(guān)人員想要通過合理的方式來對學生直觀想象能力進行培養(yǎng)。同時也可以讓學生在進行問題探究和知識解決的過程中對其進行深入的分析，要學會對數(shù)學題目和要素內(nèi)容來進行圖形的繪制。尋找到已知量和未知量之間的關(guān)系，再根據(jù)學習過的相關(guān)數(shù)學概念，在頭腦中進行合理的推理和驗證，突破平面圖形的束縛，想象在空間中這一數(shù)學模型的具體形象，這樣便于學生進行題目的解決，也就無形間發(fā)展了學生的直觀想象能力。

四、利用圖形變換提升直觀想象能力

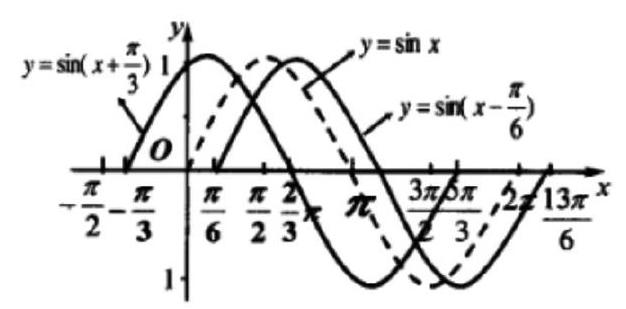
在圖形加工和變換的過程中，教師可以抓住重要因素來對有難度的題型進行簡化，這對于學生數(shù)學轉(zhuǎn)化思想的形成也有著非常重要的作用。因此在高中數(shù)學教學的過程中，教師可以根據(jù)看到的圖形變化讓學生結(jié)合手動畫圖來增強學生的直觀想象能力。例如：如圖，當前是一道三角函數(shù)的圖形，教師在對學生進行引導的過程中讓學生基于圖形變化來對一些問題進行思考。y=sin（x-）是由y=sinx的圖象怎樣變換得到的，y=sin（x+）是由y=sinx的圖象怎樣變換得到的。數(shù)學教師在引導學生對圖形進行觀察的過程中，需要對當前圖形的觀察和分析中形成的基本直觀想象能力進行構(gòu)建，其次，教師也可以讓學生對圖形自主制作的過程中發(fā)展學生的數(shù)學直觀想象能力。

總之，高中數(shù)學教師需要提升對數(shù)學教學過程中學生直觀想象能力的培養(yǎng)，可以通過相應的數(shù)形結(jié)合和圖形變化來形成相對直觀想象能力，其次教師也需要對自身的教學能力進行有效的提升，為提升學生直觀想象能力奠定基礎。其次數(shù)學教師也可以對自身的教學設計和教學過程進行進一步實踐，在不斷優(yōu)化和創(chuàng)新中培養(yǎng)和發(fā)展學生數(shù)學直觀思維能力。

參考文獻

[1] 顧建華.如何在高中數(shù)學教學中培養(yǎng)學生的直觀想象能力[J].數(shù)理化解題研究，2018（24）：12-13.

[2] 徐解清.數(shù)學核心素養(yǎng)：從內(nèi)隱走向外顯——《直線和平面平行的判定》的教學思考[J].數(shù)學通報，2017，56（7）：24-27.