幾何直觀：思維可視化的有效路徑

吳靜

摘要：幾何直觀是《義務教育數學課程標準（2011年版）》中提出的十大核心概念之一。幾何直觀能使數學問題形象化、可視化，有助于發現數量之間的關系，探索解題思路或預測結果。教師要厘清幾何直觀的內涵，基于學生已有的圖形經驗和數學問題的特點，通過選圖、構圖、析圖等方面的訓練，探尋培養小學生幾何直觀能力的有效路徑。

關鍵詞：幾何直觀;思維可視化;小學數學教學

中圖分類號：G623.5 文獻標志碼：A 文章編號：1673-9094（2019）12B-0030-04

幾何直觀是《義務教育數學課程標準（2011年版）》中提出的十大核心概念之一，也是培育數學核心素養的重要內容。借助幾何直觀能使數學問題變得簡明、形象，有助于發現數量之間的關系，增進數學理解，探索解題思路或預測結果。幾何直觀是思維可視化的有效路徑。教學中，教師要引導學生利用幾何直觀解決數學問題，不斷提升學生解決問題的能力。

一、幾何直觀的內涵和價值

（一）幾何直觀的內涵

幾何直觀可以幫助學生直觀地理解數學，在推進數學問題的研究、數學發展等方面有著重要的作用。著名數學家徐利治先生指出：“幾何直觀是借助見到的或想到的幾何圖形的形象關系產生對數量關系的直接感知。”[1]孔凡哲、史寧中先生把幾何直觀看作一種數學感知能力，認為：“幾何直觀是指借助見到的（或想象出來的）幾何圖形的形象關系，對數學的研究對象（空間形式和數量關系）進行直接感知、整體把握的能力。”[2] 《義務教育數學課程標準（2011年版）》具體闡述了幾何直觀的過程和意義，明確指出：“幾何直觀是指利用圖形描述和分析問題，借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。”[3]

綜合各家觀點，幾何直觀是為了解決抽象的數學問題，利用幾何圖形描述和分析問題，以獲得對數量關系的直接感知和整體把握的能力。幾何直觀的本質是思維的直觀化、可視化，即將抽象的“數”轉換為直觀的“形”，通過對“形”的感知和心理操作，獲得數學理解，形成解題思路。

幾何直觀與數形結合是兩個不同的概念。從研究的內容而言，數形結合的思想包含著兩個方面的內涵：一方面由“數”轉化為“形”，直觀把握數量關系;另一方面由“形”轉化為“數”，利用數的精確性和算法化的優勢，探討、揭示幾何圖形的特征。幾何直觀側重體現由“數”化“形”的內容，主要解決數學問題抽象化的問題。從研究對象而言，幾何直觀解決的數學問題包括代數問題和幾何問題，文字表述的幾何問題也是幾何直觀研究的內容。

（二）幾何直觀的教學價值

幾何直觀是借助圖形直觀感知數學本質、把握數學關系的一種有效方式，是思維可視化的有效途徑，有豐富的教學價值。

1.有助于發展數學思考

數學活動的目的是促進學生思維的發展。幾何直觀通過“圖形表征”和“圖形分析”增進數學理解，促進對數學問題的思考，從而提升數學思維能力。借助幾何直觀解題時，不能只停留在對幾何圖形淺表化的感知，而要深入到數學問題本身進行圖形的選擇和分析，找到隱蔽的條件和解決問題的線索，建立數量之間的關系，獲得對問題深層思考。

2.有助于提升解題能力

幾何直觀指向數學問題的解決，對于豐富學生的解題策略、提升解題能力有積極的作用。在學生遇到抽象數學問題而止步不前時，幾何直觀能夠有效縮短數學知識的抽象性與學生思維形象性之間的距離，密切溝通“形”與“數”之間的關系，依托“形”直觀性、可視化的特點發現隱蔽的數量關系，從而解決抽象的數學問題。

3.有助于培育創新思維

幾何直觀對于培養學生的創造思維有著重要的意義。一方面，幾何直觀是對幾何圖形特征和關系的整體把握，有利于發展學生的直覺思維能力，使學生獲得解題靈感，創生新的想法;另一方面，學生在幾何直觀中的各種差異，為創造性學習提供了機會，使問題思考的方式由“單一”走向“多元”，探索路徑從“封閉”走向“開放”。

二、幾何直觀能力的培養策略與路徑

幾何直觀能力的形成不是一蹴而就的，需要經過長期的實踐積累。在日常教學中，教師要積極運用幾何直觀分析問題，幫助學生形成幾何直觀的意識，更要通過選圖、構圖和看圖的策略指導，幫助學生積累幾何直觀經驗，培育和發展學生幾何直觀的能力。

（一）選圖——多角度考量，選取恰當的幾何圖形

幾何圖形是幾何直觀的對象，適切的圖形能有效促進學生理解數學問題、探明解題思路。教學時，教師要引導學生謹慎選擇幾何圖形表征問題，凸顯數學知識的本質。

1.關注圖形與學生經驗的“匹配度”

幾何圖形內容十分豐富，包括線、面、體在內的一切形體。受圖形學習經驗的制約，不同學段的學生對幾何圖形有著不同的選擇取向。學生的圖形認知經驗是幾何直觀的基礎，只有基于學生已有的圖形經驗選圖，才能發揮幾何直觀的價值。如，低年級學生處于幾何圖形的初步感知階段，適合畫集合圖和條狀圖等半抽象的示意圖來表示數量和數量關系。中年級學生了解了線、面圖形的基本特征，中年級是發展學生幾何直觀能力的最佳時期，可選線段圖和基本平面圖形表示問題。高年級學生可以在已有的基礎上，適當選用立體圖形表征問題。

2.關注圖形與數學知識的“契合度”

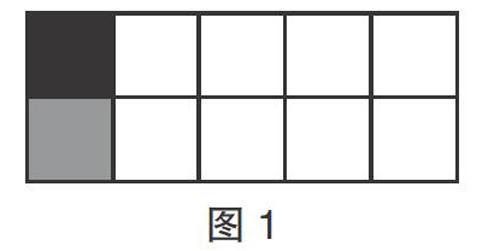
選圖表征問題時，教師要考慮與數學知識的“契合度”，直觀呈現數學知識的本質，為學生進一步分析和思考問題提供有效的支撐。如，教學除法性質時，教師可選擇長方形作為直觀載體，幫助學生理解性質背后的原理。以210÷5÷2=210÷（5×2）為例，教師借助圖1不僅能幫助學生明了先將210平均分成5分后，再將每一份平均分成2份，就是將210平均分成了（5×2）份，還能基于此圖進一步類化，幫助學生建立除法性質的幾何模型，使學生獲得對性質的一般化理解。

3.關注圖形與思維路徑的“聯結度”

選擇的圖形要與問題的思考路徑一致，能直觀啟發學生進行數學思考。教師要注意數與運算、探索規律等內容中的圖形選擇，不僅要選擇典型幾何模型，還要針對特殊解法選擇適合的直觀圖形，幫助學生克服思維定式，靈活選擇方法解題。如，計算1+3+5+7+9+11時，除了借助梯形圖將算式轉化為（1+11）×6÷2求和，還可以借助正方形圖將算式轉化為62，簡化計算方法。

4.關注圖形與表征習慣的“延續度”

圖形選擇既要考慮圖形的多樣性和靈活性，還要考慮圖形的針對性和普適性。教學時，教師要根據數學知識之間內在的聯系選圖，用同一類型的圖形描述相同性質的問題，幫助學生形成表征習慣。畫線段圖是表征倍數關系、相差關系以及行程問題等的重要方式，圖形題也不例外，可以解決如“一個等腰三角形，頂角是底角的2倍，這個三角形的底角和頂角各是多少度？”等問題。長方形、正方形示意圖適用于解決與乘法運算相關的問題，包括解釋積的變化規律和乘法結合律等。

（二）構圖——多層面切入，用幾何圖形表征數學問題

在選定合適的幾何圖形后，根據問題的特點構造圖形是培養幾何直觀能力的關鍵。教師在平時的教學中要有意識地將內隱的構圖策略顯性化，幫助學生積累構圖經驗，掌握構圖技巧，進而發展構圖能力。

1.豐富構圖經驗

很多學生無法借助幾何圖形正確表征數學問題，究其原因是缺乏相應的構圖經驗。學生的構圖經驗來源于日常的生活經驗和圖形的學習經驗，兩者缺一不可。教師要積極滲透畫圖技巧，幫助學生獲得構圖的間接經驗，也要及時發現生活經驗的不足并增補相關內容。如面對“一個正方形菜地，邊長增加3米，面積增加39平方米。原來長方形菜地面積是多少平方米？”時，教師要通過再現實際情境，幫助學生彌補生活經驗的缺失，形成正確畫圖的方法。

2.把握構圖要素

為了能使復雜的數學問題變得簡明、形象，促進學生的數學理解，教師需要對學生構圖進行指導，包括數與形的結合、關鍵信息的標示以及隱蔽條件的呈示等。一要精準刻畫、如實描述題目的有效條件及問題;二要在圖上標示出題中的每個數據，特別是解決非圖形問題時，要做到“有形必見數”，養成數形結合共同表征問題的習慣;三要關注隱蔽條件的表征，學會將隱蔽的關系外顯。如用圖表示“一個等腰三角形頂角比底角大20°，求頂角和底角的度數”時，學生要清楚標出“三角形內角和180度”這個隱藏著的信息。

3.明晰構圖順序

構圖過程實際上是梳理題目信息，再次明確題意的過程。構圖的順序能反映學生的思維狀態和水平。通常，構圖能力較差的學生只關注“細節描畫”而忽略“整體構造”，按部就班表征問題信息，導致陷入“只見樹木不見森林”的迷局。教學中，教師要引導學生按先“整體”再“局部”的順序構圖，建立各個數量之間的層級關系。如用長方形描述“一個長方形操場長100米、寬80米，長增加3米，寬增加2米，面積增加了多少平方米？”等問題時，學生要先明確長、寬變化后仍然是一個長方形，再根據長、寬的增減變化確定變化后長方形的長和寬，最后再勾畫出整個圖形。同理，用線段圖描述“行程問題”時，學生要在明確對象運動時間、地點和方向的情況下，著重表征行走的路程，確立路程和距離之間的關系。

4.變換構圖方式

不同的構圖方式在啟迪學生思維方面有著不同的價值。在學生無法借助幾何圖形直觀理解數量關系時，教師要突破常規思路的限制，根據題目特點靈活調整構圖方式，幫助學生理清關系。如教學“一筐梨，小紅第一次吃了一半多2個，第二次吃了剩下的一半少2個，最后剩下5個，原來一筐梨有多少個？”，由于題目中的信息多、關系復雜，僅用一條線段表征問題中所有的信息，很難發現數量之間的關系。如果換成多條線段表征信息（如圖2 ），并將“一半”、每次“拿走”的信息用長虛線、大括號凸顯，就能使關系明朗化，幫助學生順利解題。

（三）析圖——多路徑探索，借圖形關系把握數量關系

“并非畫出幾何圖形就可以稱為借助幾何直觀，而是需要借助幾何圖形發現所研究圖形的本質、關系或規律。”[4]幾何直觀不僅要借助圖形表征數學問題，還要利用對圖形的觀察和分析，尋求解決問題的思路和方法，直至獲得結論。教學中，教師要引導學生利用幾何直覺，結合圖形特征運用圖形變換和幾何推理等方式，幫助學生獲得看圖分析問題的能力。

1.利用幾何直覺探明方向

借助于幾何圖形的形象直接感知數學研究對象，能獲得對數量關系的直觀感知和直覺判斷，以及對結果的預測。教師要重視幾何直覺在直觀中的作用，鼓勵學生根據現有的圖形信息大膽猜測數量關系，把握研究方向并預測結果。如教學圓面積時，教師可在學生明確圓面積和圓的半徑r有關的基礎上，出示邊長為r的正方形，讓學生猜測圓面積和正方形面積之間的關系，以此確定圓面積的范圍在2r2～4r2之間，再以此為研究起點將圓無限等分后轉化成近似長方形，推導出圓面積計算公式。

2.根據圖形特征探尋關系

幾何圖形具有過程和概念的意義，更利于學生探索解題思路。在借助幾何直觀解決問題時，教師不僅要確認學生對圖形特征有準確、清晰的認知，還要引導學生基于已有圖形信息，根據圖形特征進行聯想和推測，發現隱蔽的數量關系，獲得解決問題的線索。在圖形教學時，教師就要有意識地讓學生根據圖形特征聯想關系。如，在認識圓時，教師就可以讓學生進行“根據給出的數據，你還想到了什么”的信息聯想訓練（如圖3 ），溝通長方形長、寬與圓的半徑、直徑之間的關系以及正方形邊長和圓的直徑之間的關系，為看圖分析并解決稍復雜的圓的實際問題積累思維經驗。

3.結合圖形運動探索思路

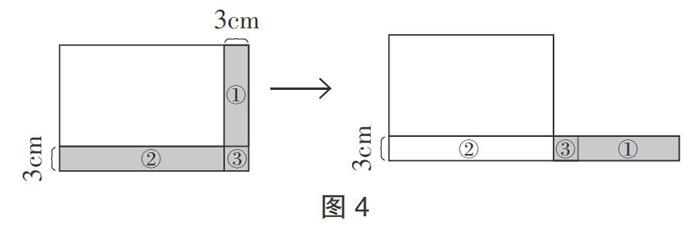
利用圖形的運動進行圖形轉化，常常能“化腐朽為神奇”，瞬間使復雜的數學關系變得簡單明了。教師要引導學生用運動的眼光看待數學問題，發現更加簡單、有效的解題路徑，發展空間想象力。如，解決“一塊長方形菜地，長和寬都增加3米后，面積增加69平方米，原來長方形菜地的周長是多少米？”（見圖4 ），在用長方形示意圖描述問題，將增加部分面積分成3個部分后，學生就需要借助圖形的旋轉，將①部分旋轉至②部分的右側，與②部分拼成一個寬為3米的大長方形，先求出長方形的長（原長方形的長與寬的和），進一步求出原長方形的周長。在解決立體圖形問題時，學生也需要通過圖形的運動，將三維立體圖形問題轉化成二維平面圖問題，從而找到解決問題的最優策略。

借助幾何圖形“看”出數量關系是一種智慧，更是一種能力。教師要加強幾何直觀的策略指導，讓學生掌握用圖表征問題的一些基本技巧，獲得畫圖的基本技能;還要通過創設適當的問題情境，幫助學生主動產生幾何直觀的意識;更要提供利用幾何直觀表達和交流數學問題的機會，讓學生在嘗試開展圖形表征、分析的過程中，在對比辨析中，不斷提升幾何直觀水平。

參考文獻：

[1]徐利治.談談我的一些數學治學經驗[J].數學通報， 2000（5）：2.

[2]孔凡哲，史寧中.關于幾何直觀的含義與表現形式——對《義務教育數學課程標準（2011年版）》的一點認識[J].課程·教材·教法， 2012（7）：93.

[3]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社， 2012：6.

[4]史寧中.例說小學數學中的幾何直觀[J].小學數學， 2017（10下）：4.

責任編輯：石萍

Geometric Intuition： An Effective Way of Thinking Visualization

WU Jing

（Jiangyin Chengjiang Central Primary School， Jiangyin 214400，China）

Abstract：? Geometric intuition is one of ten core concepts proposed by Mathematics Curriculum Criterion in Compulsory Education （2011 version）， which can make mathematic problems concrete and visualized， helping students discover the relationships between quantities， explore solutions and anticipate results. Teachers should clarify the connotations of geometric intuition and train students ability of selecting， structuring and analyzing graphs on the basis of students previous? experience and the features of mathematic problems， trying to find the effective ways of cultivating students competence of geometric intuition.

Key words： geometric intuition; thinking visualization; primary school mathematics teaching