淺談幾何畫板在中職數學教學中的應用

于升平

【摘要】隨著科學技術的發展，現代科學技術正在改變中職學生的課堂.幾何畫板作為重要的數學應用軟件，能夠清晰展示和探索數學知識.然而目前的應用并沒有得到很好的推廣及應用，筆者認為主要原因是一線教師對幾何畫板的應用模式了解不足，筆者認為幾何畫板在中職數學教學中主要的應用模式有認知模式和技能模式.

【關鍵詞】幾何畫板；中職數學；應用模式

一、幾何畫板在中職數學教學中的應用現狀

2009年頒布的《中等職業學校數學教學大綱》的“教學方法建議”中提出：要根據不同的數學知識內容，結合實際地充分利用各種教學媒體，進行多種教學方法探索和實驗.隨著電教化的發展，信息技術已經逐步進入數學教學課堂，并且正在改變著我們的課堂.目前數學教師較熟悉的課件制作軟件有word、PowerPoint、幾何畫板和Z+Z智能教育平臺，其中在數學課堂上應當發揮主要作用的幾何畫板，從數學教師的熟悉程度到應用程度上，都沒有發揮出其應有的水平.筆者指出：這與很多教育專家的期望——幾何畫板應是數學教學的主力軍，相差甚遠.這表明數學教師的一些簡單的數學教學軟件的培訓工作亟待深入.

二、應用方式

幾何畫板是一個通用的數學、物理教學環境，提供豐富而方便的創造功能使用戶可以隨心所欲地編寫出自己需要的教學課件.軟件的特點有學習容易，操作簡單，無須編程，具有一定的互動性，為幫助一線教師實現其教學思想提供了可能.根據布盧姆教學目標分類理論，依據幾何畫板在教學過程中提供的作用，筆者認為幾何畫板在中職數學教學中主要的應用模式有認知模式和技能模式.

（一）認知模式

幾何畫板是以數學邏輯為基礎的數學軟件，能夠動靜結合地展現知識的生成過程.對于理解難度較大的數學知識有很好的輔助作用.中職學生數學素養不高，對于函數的理解特別是圖像的理解難度較大.幾何畫板可以改變原有課堂中有限個點的困擾，向學生演示出無限個點的特征，從而便于學生理解.

例1 畫出正弦函數y=sinx的圖像.

分析 對于曲線的形成，由有限的點很難得出其圖像的特征，而幾何畫板可以實現曲線的形成，同時也能幫助學生理解正弦函數的定義.

教師操作：（1）打開幾何畫板，“繪圖”——“定義坐標系”，建立平面直角坐標系；

（2）打開“繪圖”——“繪制點”，繪制點O（-2，0），A（-1，0）；

（3）依次選中點O，點A，打開“構造”——“以圓心和圓周上的點繪圓”，得到單位圓O；

（4）選中圓O，打開“構造”——“圓上的點”，得到圓上一動點B；

（5）依次選中橫軸和點B，打開“構造”——“垂線”，選中垂線和橫軸，打開“構造”——“交點”，得交點C；

（6）選中垂線，打開“顯示”——“隱藏對象”，選中點B和點C，打開“構造”——“線段”；得線段BC，根據正弦函數定義，此時∠AOB的大小等于弧AB的長，∠AOB的正弦值等于點B的縱坐標；

下面在平面直角坐標系中以∠AOB的大小為橫坐標，以∠AOB的正弦值為縱坐標，構造無數多點顯示出正弦函數的圖像；

（7）依次選中點A、圓O和點B，打開“構造”——“圓上的弧”；選中弧AB，打開“度量”——“弧長”；

（8）選中弧AB的長，打開“變換”——“標記距離”，選中原點，打開“變換”——“平移”，得點D，此時OD=弧AB的長；

（9）依次選中C，D兩點，打開“變換”——“標記向量”，選中線段BC和點B，打開“變換”——“平移”，得點B′；

（10）選中B′，打開“顯示”——“追蹤點”，此時移動點B就能得到無數多個B′的圖像，從而得到正弦函數的圖像，同時也便于理解運動軌跡和圖像的關系.

（二）技能模式

美國教育家杜威提出“從做中學”的教學理念，提倡學生通過實踐獲得知識.現代數學教育理論認為，學數學就是做數學.所謂，做數學，即把數學課堂教學設置成一種活動，強調學習數學是一個現實的體驗、理解和反思的過程，強調以學生為主體的學習活動對學生理解數學的重要性，認為學生的實踐、探索與思考是學生理解數學的重要條件.因此，我們的數學教學應注重讓學生“在做中學數學，讓學生在做中感悟，做中理解，做中解決，做中發展”.同時，《中等職業學校數學教學大綱》中“課程教學目標”指出：培養學生的計算技能、計算工具使用技能和數據處理技能，培養學生的觀察能力、空間想象能力、分析與解決問題能力和數學思維能力.幾何畫板為教師和學生提供了一個理想的實驗空間，讓學生能夠通過簡單的操作體驗數學經驗的獲得.比如，通過實驗再對性質進行歸納總結，更加直觀，同時也方便總結.

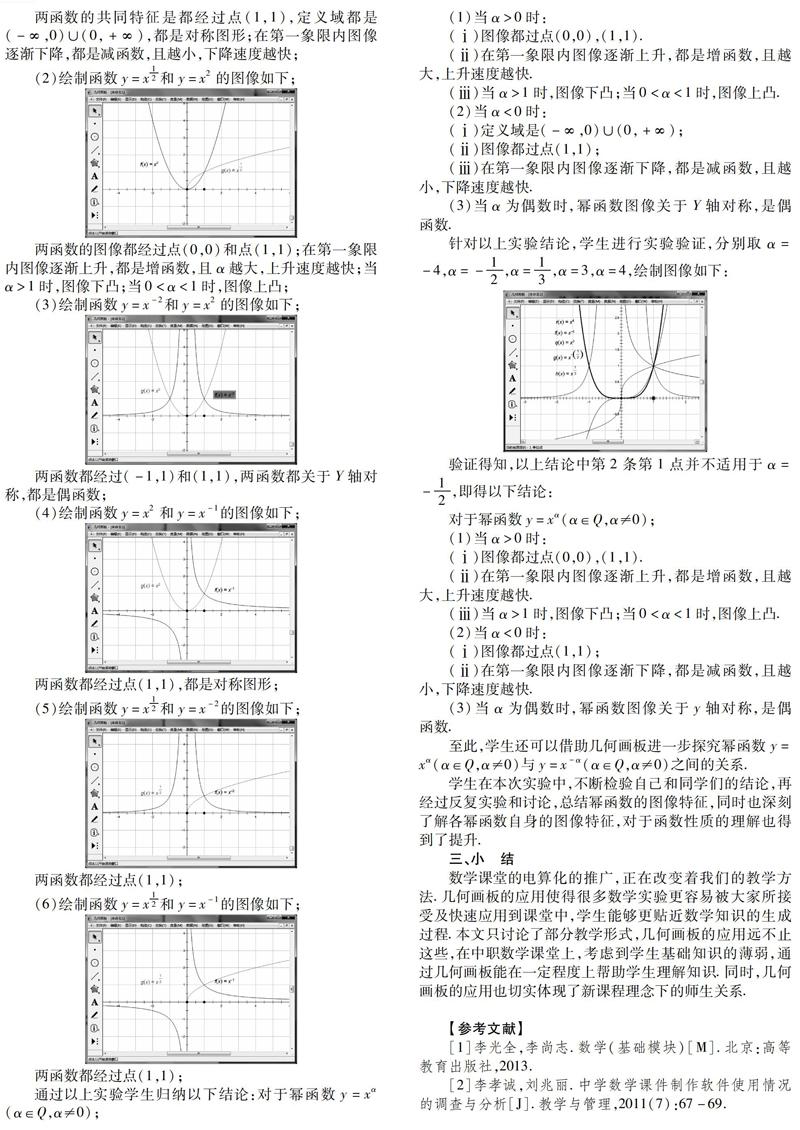
學生在本次實驗中，不斷檢驗自己和同學們的結論，再經過反復實驗和討論，總結冪函數的圖像特征，同時也深刻了解各冪函數自身的圖像特征，對于函數性質的理解也得到了提升.

三、小 結

數學課堂的電算化的推廣，正在改變著我們的教學方法.幾何畫板的應用使得很多數學實驗更容易被大家所接受及快速應用到課堂中，學生能夠更貼近數學知識的生成過程.本文只討論了部分教學形式，幾何畫板的應用遠不止這些，在中職數學課堂上，考慮到學生基礎知識的薄弱，通過幾何畫板能在一定程度上幫助學生理解知識.同時，幾何畫板的應用也切實體現了新課程理念下的師生關系.

【參考文獻】

[1]李光全，李尚志.數學（基礎模塊）[M].北京：高等教育出版社，2013.

[2]李孝誠，劉兆麗.中學數學課件制作軟件使用情況的調查與分析[J].教學與管理，2011（7）：67-69.