挖掘“數(shù)列”探究價值，促進學(xué)生思維發(fā)展

邵漢民

【摘 要】“數(shù)列”是引導(dǎo)學(xué)生研究數(shù)的變化特征，培養(yǎng)學(xué)生數(shù)感，促進學(xué)生思維發(fā)展的一種學(xué)習(xí)材料。等差數(shù)列、等比數(shù)列和裴波那契數(shù)列是比較常見的三種數(shù)列。教師以文化視角進行教學(xué)實踐，可以讓學(xué)生經(jīng)歷數(shù)列規(guī)律的探究過程，有層次地促進學(xué)生的思維發(fā)展。

【關(guān)鍵詞】數(shù)列；數(shù)學(xué)文化；探究價值；思維發(fā)展

等差數(shù)列、等比數(shù)列和裴波那契數(shù)列是三種常見的數(shù)列，在生活中可以找到它們的現(xiàn)實原型，如堆成三角形或梯形的圓木堆可以看作等差數(shù)列的原型，做拉面時師傅不斷地對折拉面的過程中，拉面根數(shù)增加的情況就是一個等比數(shù)列，而大自然中大多數(shù)花朵的花瓣數(shù)，如果從少到多排列起來，居然會是一組裴波那契數(shù)列。同時，關(guān)于這三個數(shù)列，都有一些數(shù)學(xué)故事，等差數(shù)列有高斯求和的故事，等比數(shù)列有達依爾的麥粒故事，裴波那契數(shù)列有兔子繁殖的故事。如何利用好這些現(xiàn)實原型，并充分挖掘這些故事的數(shù)學(xué)內(nèi)涵，讓學(xué)生經(jīng)歷這些數(shù)列的抽象過程，促進學(xué)生的思維發(fā)展？對此，筆者進行了教學(xué)思考與實踐。

一、等差數(shù)列——初步感受數(shù)學(xué)化的過程

利用等差數(shù)列求和這一數(shù)學(xué)知識培養(yǎng)學(xué)生良好的數(shù)感，是“等差數(shù)列”學(xué)習(xí)價值的體現(xiàn)。但是，作為小學(xué)生，如果我們單純地讓學(xué)生求等差數(shù)列的和，掌握它的計算公式：和=（首項+末項）×項數(shù)÷2，似乎還沒有真正挖掘出“等差數(shù)列”的教學(xué)價值。如何通過找尋“等差數(shù)列”與現(xiàn)實模型、圖式模型之間的聯(lián)系，體驗數(shù)學(xué)與現(xiàn)實之間的內(nèi)容聯(lián)系？如何通過“等差數(shù)列求和”的簡便算法的探究與圖式變換之間的比較，形成數(shù)形結(jié)合的思維習(xí)慣？如何淡化數(shù)學(xué)形式化思維，讓學(xué)生從數(shù)學(xué)的本質(zhì)出發(fā)理解解題的思路？出于對以上問題的思考，我們基于二下年級學(xué)生的學(xué)習(xí)基礎(chǔ)，開展把等差數(shù)列求和轉(zhuǎn)化為三角形點子圖的研究。具體安排以下三個教學(xué)環(huán)節(jié)。

（一）經(jīng)歷從“等差數(shù)列”的現(xiàn)實模型到圖式模型再到數(shù)學(xué)表達的過程

1.引入主題：看照片回憶周日愉快的親子活動（掰玉米、摘黃瓜）。然后出示下面圖片。

2.引導(dǎo)觀察：說一說它們是怎么擺放的？

3.指導(dǎo)概括：能用最簡潔的符號把這些形狀描述下來嗎？

通過以上三個層次的引導(dǎo)，形成以下數(shù)學(xué)抽象的過程。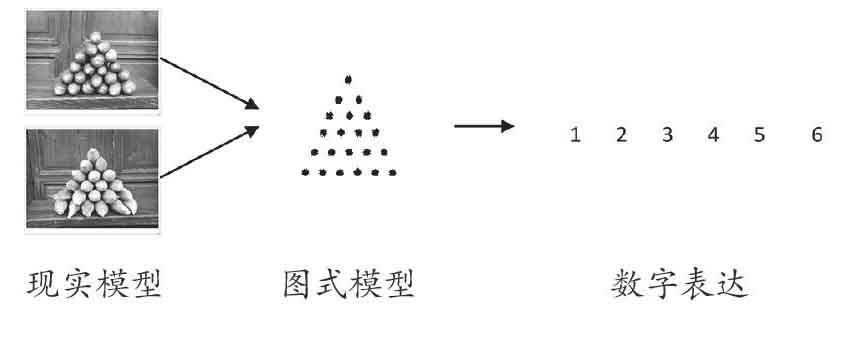

（二）探索從數(shù)學(xué)計算到圖式變換再到數(shù)形結(jié)合的歷程

1.提出問題，自主探究：一共有多少個點子？

2.交流匯報，理清思路。

1+2+3+4+5+6=（1+6）+（2+5）+（3+4）=7×3=21

（三）經(jīng)歷從變式練習(xí)到特征比較再到拓展練習(xí)的進程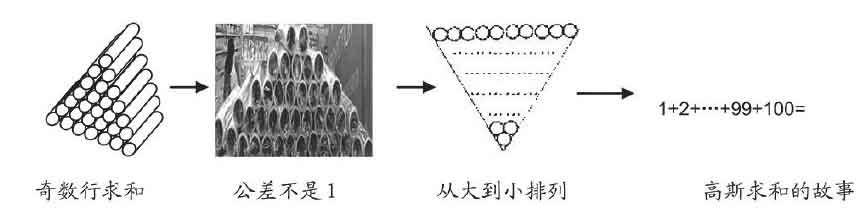

弗賴登塔爾曾明確指出：“毫無疑問學(xué)生也應(yīng)該學(xué)習(xí)數(shù)學(xué)化，當(dāng)然從最低的層次開始，也就是先從非數(shù)學(xué)內(nèi)容進行數(shù)學(xué)化，以保證數(shù)學(xué)的應(yīng)用性，同時還應(yīng)該進到下一層次，即至少能對數(shù)學(xué)內(nèi)容進行局部組織。”以上三個環(huán)節(jié)的教學(xué)設(shè)計，體現(xiàn)了弗賴登塔爾的這一數(shù)學(xué)教學(xué)思想。由此，我們在對如“數(shù)列”這樣一些高度抽象的數(shù)學(xué)化材料的處理上，不能只囿于數(shù)學(xué)公式的推理，而應(yīng)該從更普遍意義上來理解，即如何讓學(xué)生經(jīng)歷數(shù)學(xué)思維的全過程。

二、等比數(shù)列——進一步感受數(shù)學(xué)化的過程

不熟悉“幾何級數(shù)”的變化特點，茫然地做出承諾，就會釀成大錯，這樣的事例，我們可以從一些數(shù)學(xué)科普讀物中找到，如下面列舉的“達依爾的麥子”就是一個很好的教學(xué)材料。

相傳古印度人達依爾發(fā)明了國際象棋而使當(dāng)朝的國王十分開心，國王便決定重賞他。

“我不要您的重賞，陛下。”達依爾接著說，“我只要您能在我的棋盤上賞些麥子：在第一格放一粒，第二格放2粒，第三格放4粒，以后每格放的麥粒都比它前面一格多一倍，我只求能放滿64格就行了。”

“區(qū)區(qū)小數(shù)，幾粒麥子，這有何難，……”國王未加思考立即允道。

有句話叫作“君無戲言”。如果國王的賞賜真的要實現(xiàn)，那么就算國王傾全國的財富，也滿足不了對達依爾的賞賜。

對于這樣一則數(shù)學(xué)故事，如果將其轉(zhuǎn)化成教學(xué)過程，把目標(biāo)停留于求解，那么就變得太難了，對于六年級的小學(xué)生來說不免顯得力不從心，也沒有必要。但如果除去這種純粹難度外，這里包含著太多的數(shù)學(xué)化的過程。如果從這個角度來思考，等比數(shù)列的教學(xué)目標(biāo)不只是為了求出問題的解，而是在求問題解的過程中，經(jīng)歷數(shù)學(xué)化的過程。

（一）從數(shù)的表達到式的表達

小學(xué)計算中一般以數(shù)為基本單位，因此由題意可以分析得出每格中所放的麥子數(shù)依次為1，2，4，8，16，32……一直到第64格上放的麥子數(shù)這樣一組等比數(shù)列。這樣的表示方法可以讓人明顯地感受到數(shù)的大小變化，但是越往后數(shù)的位數(shù)越來越多，書寫越來越不方便。能否用更簡捷的方法來表示結(jié)果？從分析數(shù)的特征入手，從4開始，每個數(shù)都可以表示成若干個2相乘的形式。如下圖。

這個規(guī)律可以有兩種表達，即用乘法的形式表示和用冪的形式表示。通過以上三種表示每格中麥子數(shù)的方法的比較，既可以發(fā)現(xiàn)它們之間的聯(lián)系，更可以體會到數(shù)學(xué)表達的優(yōu)化過程。

誠然，對于六年級的小學(xué)生來說，也只學(xué)到平方數(shù)與立方數(shù)的表達，對于如63個2相乘的運算用冪的形式來表示，還是很陌生。但是，如果我們能運用遷移的思路，讓學(xué)生理解平方數(shù)與立方數(shù)的基本結(jié)構(gòu)，類比“乘方”這種運算形式簡寫式an，也是可以實現(xiàn)的。

（二）從按運算順序直接計算到用遞推法找規(guī)律簡算

在計算其結(jié)果時，一般我們用邏輯推理的形式來進行教學(xué)。

從以上列舉中發(fā)現(xiàn)，“前幾項的和等于后一項的數(shù)減1”，所以棋盤上64格上的麥粒數(shù)的和等于第65格上的麥粒數(shù)減1，即264-1。

就數(shù)學(xué)思維而言，以上解決問題的形式是一種數(shù)學(xué)演算的過程，是解決等比數(shù)列的一種解題過程。如果從方法論的角度來思考，解決這一個問題可以用方法一、方法二進行簡化計算。

以上三種方法，從計算的簡捷性來看，當(dāng)然是前兩種方法更加優(yōu)越，但從小學(xué)生的可接受性來說，方法二更好。因此，在實際教學(xué)中我們要引導(dǎo)學(xué)生用方法二來思考。

可以直接提出要求：現(xiàn)在請同學(xué)們計算出結(jié)果。1分鐘之后，請學(xué)生匯報計算情況，從學(xué)生的匯報中得到方法二中的學(xué)習(xí)材料，再組織學(xué)生討論。

（三）從計算出結(jié)果到感受大數(shù)

最后結(jié)果的計算，可以借助于計算器。這些麥粒的總數(shù)為1+2+22+23+……+263=264-1=18446744073709551615粒。

一個20位數(shù)，這么多麥粒究竟有多少？光看這個數(shù)，可能并不能感受到有多少。就如我們?nèi)说穆犛X，當(dāng)聲音的頻率過高與過低時都不可能聽清楚一樣，當(dāng)一個數(shù)過大或過小時，我們也不可以用具體的表象進行感知。

那么，如何讓學(xué)生感知到這個數(shù)的大小？

方法一是把單位變大，如20000粒左右的麥子大約是1千克，那么一噸麥子就是20000000粒，這樣一除，18446744073709551615粒麥子大致上是922 327 203 685噸。

第二種方法是進行形象化的描述，也就是說大約需要九千二百二十三億噸麥子才能滿足達依爾的要求。這大約是全球兩千年所產(chǎn)小麥的總量。

這讓區(qū)區(qū)一個印度國王如何賞得起呢？

三、斐波那契數(shù)列——培養(yǎng)學(xué)生的數(shù)學(xué)反思習(xí)慣

在數(shù)學(xué)史料中，有許多數(shù)學(xué)家編制過數(shù)學(xué)題，其中有一些題目，如果從自然現(xiàn)象與自然規(guī)律來看，是不符合客觀規(guī)律的，甚至是十分荒唐的，如“雞兔同籠”問題，雞和兔關(guān)在同一個籠子里，這是不合常理的。那么數(shù)學(xué)家為什么要編制這樣的題目，其真正的價值是怎樣的？我們可以從對斐波那契數(shù)列的分析中找到答案。

假定一對剛出生的小兔一個月后就能長成大兔，再過一個月便能生下一對小兔，并且此后每個月都生一對小兔。一年內(nèi)沒有發(fā)生死亡，問一對剛出生的兔子，一年內(nèi)能繁殖多少對兔子？

如果從生物學(xué)的角度來看待這個問題，這是一件十分荒唐的事情，小兔子一個月后并不能變成大兔，母兔一般一次可以生育5～6只小兔。總之，兔子不會按斐波那契所說的這樣有規(guī)律地生長與生育。這也正是這道名題受到人們質(zhì)疑的原因，因為它所展現(xiàn)的情境不符合實際。

如果從數(shù)學(xué)的角度來講，問題情境有兩個用途，一是體現(xiàn)數(shù)學(xué)的實用價值，二是為數(shù)學(xué)知識構(gòu)建一個現(xiàn)實原型。當(dāng)然兩者能夠兼顧更好。斐波那契數(shù)列中的問題情境，顯然是后者。數(shù)學(xué)家編制這樣一個問題，是讓解題者感受到，在解決紛繁復(fù)雜的問題時，如果能找到規(guī)律，就可以根據(jù)規(guī)律進行推理。斐波那契數(shù)列的教學(xué)價值就在于此。

下面是我們設(shè)計的教學(xué)過程。

1.理解題意，獨立解答。

教師談話引入題目，請學(xué)生讀題，說說題目的意思。然后請學(xué)生獨立解答。

2.交流方法，發(fā)現(xiàn)規(guī)律。

一般學(xué)生會有以下三種基本思路。

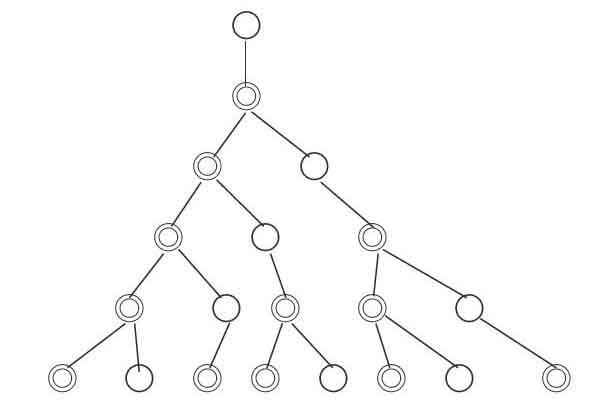
（1）圖示法

我們用◎表示一對大兔，用○表示一對小兔，逐月統(tǒng)計兔子的對數(shù)：

第1月底

第2月底

第3月底

第4月底

第5月底

第6月

……

（2）列表法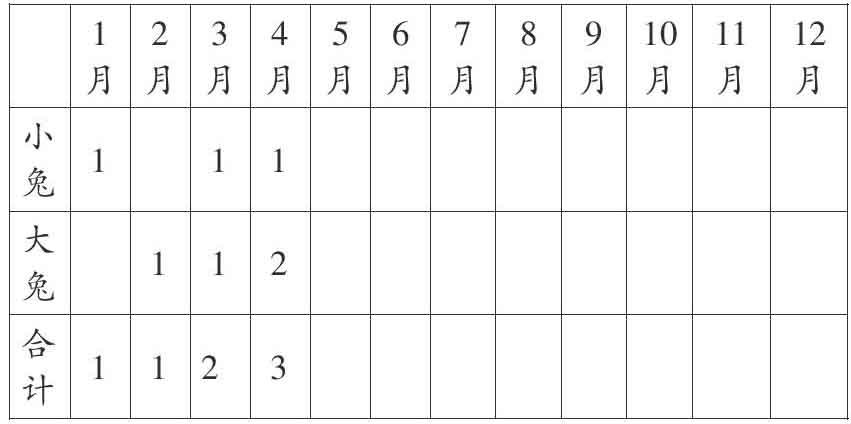

（3）列舉法

一月，只有1對小兔，大兔為0對，合計1對；

二月，1對小兔長成1對大兔，小兔變?yōu)?對，大兔1對，合計1對；

依此類推：

三月：小兔有1對；大兔有1對；合計1+1=2（對）；

……

不論用哪一種方法，只要花時間，學(xué)生均可以推導(dǎo)出最后的結(jié)果。但這并不是本題在小學(xué)教學(xué)中的真正用意。本題的真實用意應(yīng)該是培養(yǎng)學(xué)生的反思意識，能從前幾個月結(jié)果之間的關(guān)系，發(fā)現(xiàn)規(guī)律。

因此，可以讓學(xué)生解決到中途，或有個別學(xué)生解答出結(jié)果時，讓學(xué)生停一停，反思自己已知的結(jié)果，從中找一找規(guī)律。如果發(fā)現(xiàn)了規(guī)律，可以根據(jù)規(guī)律推導(dǎo)出下一個結(jié)果，并用原來的方法進行驗證。這是解決問題時很重要的思維習(xí)慣。通過觀察學(xué)生找到了規(guī)律：

第三個數(shù)起，后一個數(shù)都是前兩個數(shù)的和。即1，1，2，3，5，8，13，21，34，55，89，144……

為了紀念這位數(shù)學(xué)家，這個數(shù)列后來便以斐波那契的名字命名，叫作斐波那契數(shù)列。數(shù)列的每一項，則稱為“斐波那契數(shù)”。第十二位的斐波那契數(shù)，即為一對剛出生的小兔，一年內(nèi)所能繁殖的兔子的對數(shù)，這個數(shù)為144。前面的幾個斐波那契數(shù)分別是1，1，2，3，5，8，13，21，34……

3.聯(lián)系自然，感受神奇。

接著可以結(jié)合圖示向?qū)W生展示自然界中的斐波那契數(shù)。

斐波那契數(shù)列在它誕生的近800年間，由于它的神奇，引來無數(shù)的“斐迷”，驅(qū)使他們不僅在數(shù)學(xué)領(lǐng)域研究它，更有人從自然領(lǐng)域、化學(xué)領(lǐng)域和科學(xué)領(lǐng)域去探究它的奇妙。

綜合以上的思考與教學(xué)，當(dāng)我們在指導(dǎo)學(xué)生進行課外閱讀或進行數(shù)學(xué)課外延伸教學(xué)的時候，不要只是從知識的層面來看某些內(nèi)容可用還是不可用，而要深入到其中的思維層面，看其是否能促進學(xué)生的思維發(fā)展。

（浙江省杭州市蕭山區(qū)所前二小 311200）