利用多樣化算法，培養(yǎng)學(xué)生數(shù)學(xué)核心素養(yǎng)

邢艷++范文貴

【摘 要】原創(chuàng)一道網(wǎng)格背景下多種算法解決多邊形面積的題目，可以有助于培養(yǎng)學(xué)生的數(shù)學(xué)核心素養(yǎng)。具體而言，可以通過以下路徑展開：研發(fā)學(xué)習(xí)素材，為學(xué)生創(chuàng)設(shè)研究問題的空間；鼓勵獨立思考，培養(yǎng)科學(xué)精神；在個性化解法的生成中，培養(yǎng)學(xué)生勇于探索的精神；在算法多樣化的交流中培養(yǎng)學(xué)生理性思維；在活動經(jīng)驗的積累中，培養(yǎng)學(xué)生批判質(zhì)疑的精神。特別是當(dāng)學(xué)生遇到看似無法解決的問題時，鼓勵學(xué)生探索問題解決的新途徑，培養(yǎng)學(xué)生反思問題的解決過程，從而更好地感悟?qū)W習(xí)方法。

【關(guān)鍵詞】網(wǎng)格多邊形；數(shù)學(xué)核心素養(yǎng)；問題解決；理性思維

數(shù)學(xué)核心素養(yǎng)是以培養(yǎng)能夠適應(yīng)現(xiàn)代社會生活的公民為目標(biāo)，以教育各階段相應(yīng)的數(shù)學(xué)核心知識為載體，培養(yǎng)學(xué)生數(shù)學(xué)創(chuàng)新能力，激發(fā)學(xué)生主動思考的意識，形成積極的數(shù)學(xué)態(tài)度，并為學(xué)生的可持續(xù)發(fā)展提供強有力的支撐。在小學(xué)數(shù)學(xué)課堂教學(xué)中落實數(shù)學(xué)核心素養(yǎng)應(yīng)注重培養(yǎng)小學(xué)生理性思維、批判質(zhì)疑、勇于探索的科學(xué)精神，以及在反思中學(xué)會學(xué)習(xí)，在問題解決中實踐創(chuàng)新。

一、研發(fā)學(xué)習(xí)素材，創(chuàng)設(shè)研究問題的空間

好的學(xué)習(xí)材料能喚醒學(xué)生原有的數(shù)學(xué)活動經(jīng)驗，并能主動運用經(jīng)驗去解決新的問題，從而觸發(fā)其積極思維、主動參與，并在思考與解決問題的過程中形成多元的、獨特的問題解決方案，使后續(xù)的交流碰撞、實現(xiàn)經(jīng)驗的優(yōu)化與提升成為可能。我們原創(chuàng)了一道網(wǎng)格背景下多種算法解決多邊形面積的題目。

圖1中每個方格的面積為1cm2，請同學(xué)們用多種方法求這個多邊形的面積。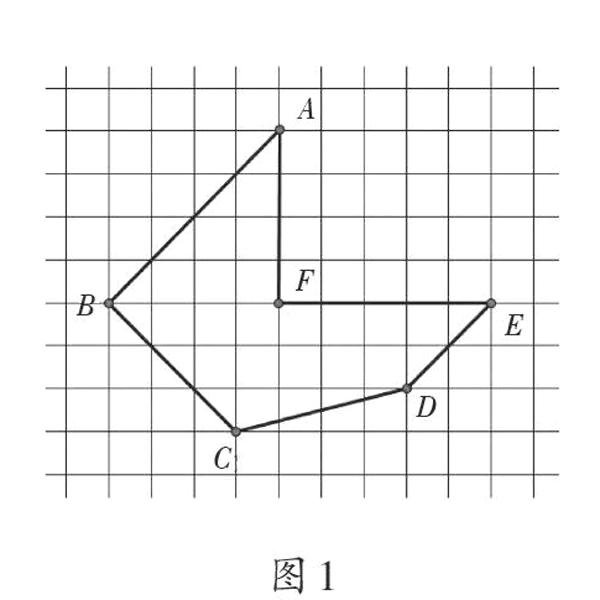

該原創(chuàng)題為解決問題方法的多樣性提供了可能，同時在學(xué)生將組合圖形割補為基本圖形的過程中，所學(xué)過的基本圖形都將一一呈現(xiàn)，使得教學(xué)過程更為系統(tǒng)、完整。

二、鼓勵獨立思考，培育科學(xué)精神

科學(xué)精神主要是學(xué)生在學(xué)習(xí)、理解、運用科學(xué)知識和技能等方面所形成的價值標(biāo)準(zhǔn)、思維方式和行為表現(xiàn)。具體包括理性思維、批判質(zhì)疑、勇于探究等基本要點。

（一）在個性化解法的生成中培養(yǎng)勇于探索的精神

在算法多樣化的教學(xué)中，教師應(yīng)尊重學(xué)生的個性特征，給予學(xué)生獨立思考的機會，激勵學(xué)生自主探索，允許不同的學(xué)生從不同的角度認(rèn)識問題，以不同的方式表達問題，用不同的方法探索問題，使學(xué)生個體盡可能找到自己的算法。

在獨立思考的過程中，有的學(xué)生在方格紙上分割出第一種方法（如圖2），計算時卻發(fā)現(xiàn)“三角形FCD的底和高是多少”不能確定，求不出三角形的面積。他立即改變思考的角度，方格紙上又呈現(xiàn)出第二種、第三種、第四種方法，他又發(fā)現(xiàn)這三種方法中也都出現(xiàn)了類似于第一種方法的問題，即在分割的圖形中總有一個三角形的底和高不能確定，求不出三角形的面積。在一次又一次地探索中，終于，他尋求到了能計算出這個多邊形面積的方法。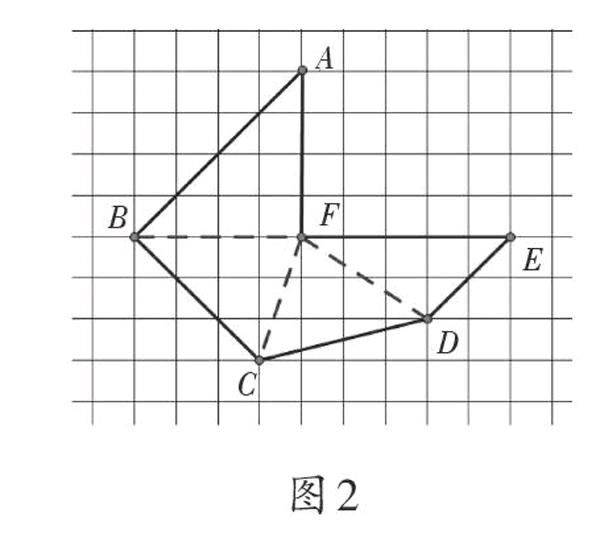

也有的學(xué)生認(rèn)為自己的方法雖然能計算出多邊形的面積，但比較煩瑣，通過不斷地改變輔助線，最終簡化了分割方法。

還有的學(xué)生除用分割法轉(zhuǎn)化圖形外，又使用添補法轉(zhuǎn)化圖形。

核心素養(yǎng)是一個融知識、技能、態(tài)度和價值觀于一體的集成系統(tǒng)，在價值觀的推動下，學(xué)生對數(shù)學(xué)問題產(chǎn)生好奇心和想象力；他們不畏困難，堅持不懈地探索；在運用知識與技能的過程中，大膽嘗試，積極尋求有效解決問題的方法。這樣學(xué)生才能形成相應(yīng)的數(shù)學(xué)素養(yǎng)。

（二）在算法多樣化的交流中培養(yǎng)理性思維

學(xué)生提出各種個性化的算法后，教師組織學(xué)生互動交流，以歸納整理出“多樣化”的算法。學(xué)生不僅能認(rèn)識從不同角度得出算法，而且能更好地展開交流和討論，期間進行糾正、補充和完善，共同分析探究過程，評價探究結(jié)果，分享探究成果。

在互動交流的過程中，教師與學(xué)生一起將多樣的方法按轉(zhuǎn)化的角度不同分成三類。

第一類，從圖形內(nèi)部尋找解決問題的路徑。

（1）以“BF”“MD”為主線的分割方法（如圖3）。

（2）以“BF”“OC”為主線的分割方法（如圖4）。

（3）以“QM”“MD”為主線的分割方法（如圖5）。

（4）以“QC”為主線的分割方法（如圖6）。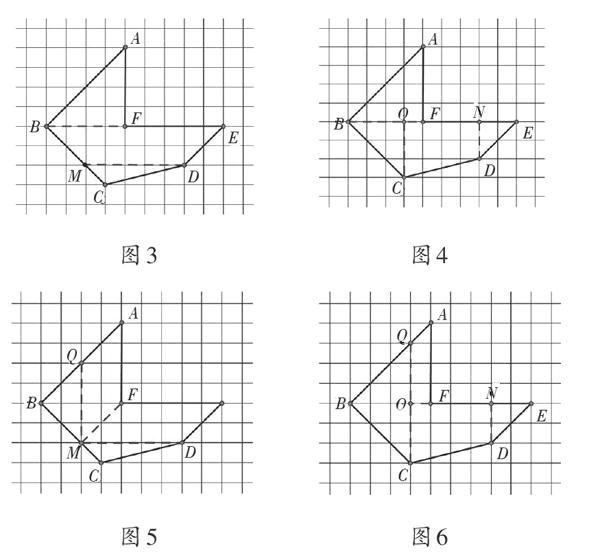

學(xué)生的關(guān)注點聚焦于圖形的內(nèi)部，用分割的方法將多邊形轉(zhuǎn)化為幾個基本圖形后再計算面積。由于觀察圖形的角度不同，分割圖形的切入點也不相同；加之學(xué)生對各種基本圖形的熟悉程度存在差異，進一步分割出的圖形亦有所不同，分割的結(jié)果有繁有簡。因此，以上這四種方法各自還包含了不同的變形。

第二類，從圖形外部尋找解決問題的路徑。

其思路是從整體觀察多邊形，在其外部添補一個長方形（如圖7）。多種變形的不同之處集中于四邊形CDEG的分割，除圖7的方法外，還可以過D點作CG的平行線交EG于M，也可以直接連接DG。

第三類，內(nèi)外綜合尋找解決問題的路徑。

將整個圖形分割為兩部分思考，上面是三角形ABF，可直接計算其面積；下面的四邊形BCDE用添補法進一步轉(zhuǎn)化后再計算面積。該方法的不同之處體現(xiàn)在四邊形BCDE的轉(zhuǎn)化思路上，有三種形成。

（1）將四邊形BCDE添補為矩形BJGE（如圖8）。

（2）將四邊形BCDE添補為直角梯形BCGE（如圖9）。endprint

（3）將四邊形BCDE添補為等腰梯形BCLE（如圖10）。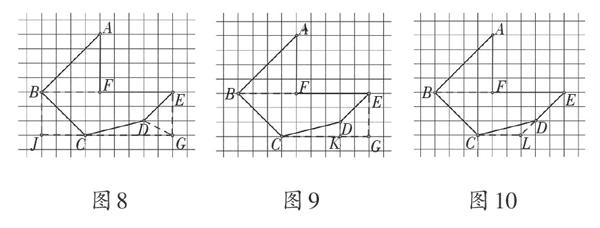

通過觀察、比較、分類，學(xué)生發(fā)現(xiàn)這些轉(zhuǎn)化方法之間的聯(lián)系與區(qū)別，并抽象、概括出每種思路的一般特點，將零散的、個別的轉(zhuǎn)化方法系統(tǒng)化和條理化，形成多維度的觀察視角。同時深刻地認(rèn)識到轉(zhuǎn)化方法在解決問題中的作用，是基于對圖形的構(gòu)成（質(zhì)）與圖形的組成形式（現(xiàn)象）的認(rèn)識，這是一個隱含了哲學(xué)思辨（現(xiàn)象與本質(zhì)的關(guān)系）的辯證唯物主義過程。在這個過程中，學(xué)生要認(rèn)識分解與組合、恒等變形，也要認(rèn)識處理現(xiàn)象與本質(zhì)的基本方法，從而感悟數(shù)學(xué)推理思想。

（三）在活動經(jīng)驗的積累中培育批判質(zhì)疑的精神

在學(xué)生的轉(zhuǎn)化方案中出現(xiàn)最多的是圖2。他們也都認(rèn)為這是“無法解答”的方法，因為無法確定三角形FCD的底和高是多少。這種方法被大家一致判斷為不可行的同時，學(xué)生中發(fā)出了“有辦法解答”的聲音。學(xué)生原本平靜的腦海，又掀起了思維的波瀾，驚訝之后又凝神沉思。

“難道你能找到三角形的底和高嗎？”

“能不能把三角形FCD轉(zhuǎn)化成我們知道的圖形并計算它的面積呢？”一石激起千層浪，在座的學(xué)生豁然開朗。

這個提出質(zhì)疑的學(xué)生，將轉(zhuǎn)化思想建構(gòu)到自己的認(rèn)知結(jié)構(gòu)中，進而遷移到解決三角形FCD的面積計算上來，才提出突破思維定勢的問題。這就是數(shù)學(xué)思想的力量，既能解決問題，又是下一個問題的孵化器。通過獨立思考，學(xué)生獲得了屬于自己的經(jīng)驗；長期活動經(jīng)驗的積累，又使學(xué)生獲得了思維方法，最終達到的目標(biāo)就是學(xué)會思考。創(chuàng)新依賴的是思考，是數(shù)學(xué)活動中創(chuàng)造性的思維。因此，獨立思考、學(xué)會思考是創(chuàng)新的核心。

三、反轉(zhuǎn)不可行，探索問題解決的新途徑

學(xué)生在學(xué)習(xí)過程中獲取前人和他人從沒有獲取的新知識、新技術(shù)、新能力或?qū)η叭撕退艘勋@取的知識有新的思路、新的理解、新的解釋和新的應(yīng)用就是創(chuàng)新。來自學(xué)生的提問把所有學(xué)生帶入激活已知、產(chǎn)生心向、激發(fā)創(chuàng)造的問題情境。

通過合作探究，學(xué)生創(chuàng)造出了四種不同的方法。

1.將三角形FCD添補為矩形OCKN（如圖11）。

2.將三角形FCD添補為直角梯形FCKN（如圖12）。

3.將三角形FCD添補為三角形FXY（如圖13）。

4.將三角形FCD在內(nèi)部分割為三個三角形（如圖14）。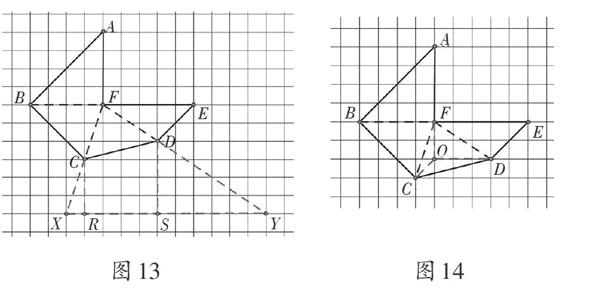

通過以上方法的轉(zhuǎn)化都可以計算出三角形FCD的面積，因此圖2的方法得解，將不可行變?yōu)榭尚校∵@四種方法對學(xué)生而言是前所未有的，彼此之間又是與眾不同的，每種方法都是個人思維水平的突破。從思路上，這四種方法反映為不同的創(chuàng)新技法，圖11和圖12屬于類比借鑒法，其思路來源于圖8和圖9的轉(zhuǎn)化方法。圖13屬于拓展解題思路，在延長三角形兩邊的過程中尋找與網(wǎng)格線重合且端點能落在小正方形頂點上的第三邊。其目的是使放大的三角形中有一條邊與網(wǎng)格線重合，就可以知道大三角形的一組底和高，進而用添補法計算面積。圖14屬于縮小思路，切入點是三角形FCD中的直角三角形FOD，它的兩條直角邊與網(wǎng)格線重合，這是有利的轉(zhuǎn)化條件。然而，這四種轉(zhuǎn)化方法的目標(biāo)都聚焦在利用與網(wǎng)格線重合的邊構(gòu)造新圖形上，比之前的轉(zhuǎn)化過程凸顯解決問題的本質(zhì)，讓我們清晰地感受到學(xué)生思維的深入和品質(zhì)提升的過程。

憑借經(jīng)驗和直覺，學(xué)生認(rèn)為“不知道三角形的底和高是多少，就不能計算三角形的面積”這個結(jié)論是錯誤的，是學(xué)生普遍存在的真問題。學(xué)生的大膽質(zhì)疑推進課堂教學(xué)的進程和思維的深入。通過對新問題的探究，其成果令人振奮，學(xué)生不僅糾正了原先的錯誤想法，認(rèn)識到底乘高再除以2是求三角形面積的一般方法，但不是唯一的方法！在挑戰(zhàn)中，學(xué)生清晰地感受到自己學(xué)習(xí)的功夫仿佛又精進了一步。原來，挑戰(zhàn)和學(xué)習(xí)被學(xué)生感知，是數(shù)學(xué)學(xué)習(xí)的必要要素，在問題解決中實踐創(chuàng)新的核心素養(yǎng)得到了培養(yǎng)。

四、反思問題解決過程，感悟?qū)W習(xí)方法

反思是對自己的思維過程、思維結(jié)果進行再認(rèn)識的檢驗過程，它是學(xué)習(xí)中不可缺少的重要環(huán)節(jié)。我們可以以三個問題引導(dǎo)學(xué)生反思。

（一）學(xué)習(xí)是思考的基礎(chǔ)，思考是學(xué)習(xí)的靈魂

“這節(jié)課我們做了哪些事？”這節(jié)課學(xué)生先通過獨立思考，自主探索解決問題的方法；然后進行比較歸納，梳理出多維度解決問題的路徑；最后通過對不可行解法的挑戰(zhàn)，實現(xiàn)了問題解決的新突破。學(xué)生的思維一刻不曾停歇。他們在思考中摸索，在思考中優(yōu)化，在思考中質(zhì)疑，在思考中創(chuàng)新，使分析綜合、比較鑒別、抽象和想象等思維能力得到全面的、均衡的發(fā)展，完整地經(jīng)歷了問題解決的全過程。

（二）獲得學(xué)習(xí)方法，是一切學(xué)習(xí)之母

“你對哪個環(huán)節(jié)印象最深？”學(xué)生一致認(rèn)為“不能把三角形FCD轉(zhuǎn)化成我們知道的圖形計算它的面積嗎？”這個問題的提出和圖11至圖14的解法令他們印象深刻。從圖2的不可行到可行解法的探索是學(xué)生對轉(zhuǎn)化方法深刻理解和熟練掌握的具體表征。學(xué)習(xí)中的創(chuàng)新就是敢于用懷疑的眼光去審視既成的事實，對已獲取的知識有新的思路、新的理解、新的解釋和新的應(yīng)用。

（三）積極的態(tài)度是學(xué)習(xí)中最有價值的財富

“你對自己最滿意的表現(xiàn)是什么？”“我能想出好幾種方法！”“我的方法最簡捷！”“我把圖2的方法變成可行的了！”……學(xué)生的暢所欲言呈現(xiàn)出積極的學(xué)習(xí)態(tài)度和勇于探索的精神。他們想學(xué)、肯學(xué)、 勤學(xué)、會學(xué)，這些可貴的學(xué)習(xí)品質(zhì)是學(xué)會學(xué)習(xí)的前提。

小學(xué)生數(shù)學(xué)核心素養(yǎng)的培養(yǎng)是一個潛移默化、日積月累、不斷發(fā)展和提高的過程。教師應(yīng)該把對小學(xué)生數(shù)學(xué)核心素養(yǎng)的培養(yǎng)落實到每一節(jié)數(shù)學(xué)課中，寓于具體數(shù)學(xué)知識技能的教學(xué)之中。既注重“有形”的數(shù)學(xué)概念、法則、性質(zhì)、定律、規(guī)律等顯性知識的教學(xué)，又要注重引導(dǎo)學(xué)生深入體悟隱藏在這些知識背后“無形”的、體現(xiàn)數(shù)學(xué)知識本質(zhì)的數(shù)學(xué)思想方法、核心素養(yǎng)。

（天津市南開區(qū)教育中心 300110

天津師范大學(xué)初等教育學(xué)院 300110）endprint