用對立統(tǒng)一的眼光看“方法的方法”

郜舒竹

【摘 要】研究解決問題的一個重要課題就是“方法是從哪里來的？”這種“元方法”的思考中蘊含著辯證唯物主義對立統(tǒng)一的思想。運用這樣的思想，思考問題中諸如多與少、亂與齊、局部與整體、動態(tài)與靜態(tài)的矛盾，并將其相互轉化，就可以得到解決問題的方法。

【關鍵詞】辯證唯物主義 解題方法 數(shù)學課程 對立統(tǒng)一

數(shù)學課程內容作為千百年來人類智慧的結晶，其中必然蘊含著大量人類富于智慧的思想，在數(shù)學教學研究中挖掘這樣的思想，并將其融入到教學與學習活動的設計中，無疑是體現(xiàn)數(shù)學課程內容人文性的重要方面。

比如，研究解決問題的一個重要課題就是“方法是從哪里來的？”數(shù)學教師經常會教導學生“要掌握方法”，但又很難說清楚“方法的來源”是什么，這種對于“方法的方法”的思考可以叫作“元方法（Meta-method）”的思考。如果把“學會學習”視為教育教學的目標之一，那么讓學生經歷并體驗“元方法”的思考，就應當成為數(shù)學教學的重要內容。

一個數(shù)學問題通常由問題的目標、問題的障礙和已知的信息構成。故此，問題解決實質上就是超越已知信息與問題目標之間的障礙，建立已知信息與問題目標之間聯(lián)系的過程。

所謂“障礙”，往往產生于思維中某種矛盾的對立狀態(tài)。辯證唯物主義關于對立統(tǒng)一的基本規(guī)律告訴我們，矛盾的雙方在一定的條件下可以互相轉化。因此，為了超越障礙，首先需要識別產生障礙的主要矛盾，并發(fā)現(xiàn)使得矛盾雙方實現(xiàn)統(tǒng)一的條件。這樣的思維方式應該成為思考解決問題方法的方法。

一、 多與少

一些數(shù)學問題呈現(xiàn)出研究對象“多”的特點，比如：在平面上畫10條直線，每兩條直線都不重合。那么最多可以形成多少個交點？缺少數(shù)學經驗的小學生遇到這樣一個問題時，通常都是在紙上嘗試去畫出10條直線，而后試圖數(shù)出交點的個數(shù)，這樣的做法很難得到正確答案，原因就是要數(shù)的交點太多。因此，“多”就成為解決這個問題的障礙。

事實上，如果只有2條直線或3條直線，一般都不會感覺困難。現(xiàn)在就出現(xiàn)了這樣的現(xiàn)象，“少”就會，“多”就不會。因此，“多”與“少”的矛盾就成為產生這個問題障礙的基本矛盾。如何處理這一對矛盾就成為解決這個問題的關鍵。

鑒于矛盾的雙方在一定的條件下可以互相轉化的啟示，因此應該去建構“多”與“少”的轉化模式，借助這種模式的建構過程，就會得到解決問題的方法。

首先從最少的1條直線的情況入手，發(fā)現(xiàn)沒有交點。

再考慮2條直線的情況，由于問題的已知信息要求“每兩條直線都不重合”，所以這2條直線的位置關系有兩種，一種是平行，另一種是相交。而平行的情況沒有交點，不符合已知信息中的“最多”。所以，2條直線的情況最多形成1個交點。

對于3條直線的情況，為了使得這種情況與前面的情況緊密聯(lián)系，應該把3條直線的情況看作在2條直線的基礎上添加1條直線。依據(jù)前面的啟發(fā)，第三條直線不能與前面的任何一條直線平行。即使如此，第三條直線的添加還會出現(xiàn)兩種情況，一種是經過前面2條直線的交點[見圖1（a）]，另一種是不經過前面2條直線的交點[見圖1（b）]。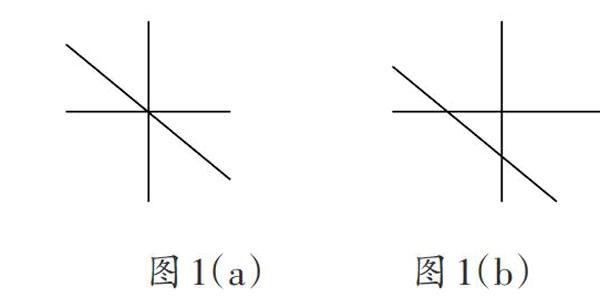

顯然，為了使得交點個數(shù)最多，第三條直線不能夠經過前面2條直線的交點。這樣就可以知道，第三條直線與前面2條直線各有1個交點，所以3條直線的情況最多形成（1+2）=3個交點。

至此，已經可以歸納出新的已知信息。為了滿足交點個數(shù)最多，所畫的直線必須符合如下兩個條件：

l 每2條直線不能平行。

l 每3條直線不能共點。

現(xiàn)在已經建構出了聯(lián)系“多”與“少”的模式，這一模式可以從下表中清晰地看出來。

解決這個問題所用到的方法，可以稱之為“從特殊到一般”或“難的不會，想簡單的”的方法。其實，它的思想基礎就是用辯證唯物主義對立統(tǒng)一的觀點處理諸如“多”與“少”“大”與“小”“遠”與“近”這樣的矛盾。

因此就可以歸納出一種思考問題解決的方法，可以稱之為“多的不會，想少的”，這也是辯證唯物主義方法論中“化難為易”的具體體現(xiàn)。

二、 亂與齊

數(shù)學中的一些問題還可能表現(xiàn)為研究對象的“亂”，比如：兩位數(shù)中十位數(shù)字大于個位數(shù)字的數(shù)共有多少個？

隨意列舉一些滿足問題要求的兩位數(shù)并不困難，比如32，96，74等。但要數(shù)出準確的個數(shù)，并非輕而易舉的。如果要數(shù)出全體兩位數(shù)的個數(shù)，并不會感覺困難，而滿足問題要求的兩位數(shù)的個數(shù)肯定少于全體兩位數(shù)的個數(shù)，為什么對象少了反而感覺困難了呢？這說明問題的主要障礙不在于“多”。更主要的原因是這些兩位數(shù)在思維中的狀態(tài)是“混亂”的，這才是問題的主要障礙。

“混亂”的對立一方應該是“整齊”。所以產生這個問題障礙的主要矛盾就應該是“混亂”與“整齊”的對立。如何把“混亂”的狀態(tài)轉化為“整齊”的狀態(tài)，形成矛盾雙方的統(tǒng)一，就成為解決這個問題的關鍵。

所謂“整齊”具有兩方面的含義，一是“類屬明確”，二是“排列有序”。好比日常生活中收拾房間時所做的“書進書柜、衣入衣柜”等，而且書在書柜中不能胡亂堆放，衣在衣柜中不能放得亂七八糟，而應該有序排列。因此，解決這個問題的過程實際上就是把十位數(shù)字大于個位數(shù)字的兩位數(shù)按照某種規(guī)則“分類、排序”。

“分類、排序”也是一種模式的建構，是抽象思維的產物。凡抽象思維的產物就具有一定的“自由度”，表現(xiàn)出來的是模式的多樣性。比如關于十位數(shù)字大于個位數(shù)字的兩位數(shù)的分類與排序，可以建構出如下不同的模式。

模式一

[十位數(shù)字 十位數(shù)字大于個位數(shù)字的兩位數(shù) 個數(shù) 1 10 1 2 20，21 2 3 30，31，32 3 4 40，41，42，43 4 5 50，51，52，53，54 5 6 60，61，62，63，64，65 6 7 70，71，72，73，74，75，76 7 8 80，81，82，83，84，85，86，87 8 9 90，91，92，93，94，95，96，97，98 9 合計 45 ]

模式二

[個位數(shù)字 十位數(shù)字大于個位數(shù)字的兩位數(shù) 個數(shù) 0 10，20，30，40，50，60，70，80，90 9 1 21，31，41，51，61，71，81，91 8 2 32，42，52，62，72，82，92 7 3 43，53，63，73，83，93 6 4 54，64，74，84，94 5 5 65，75，85，95 4 6 76，86，96 3 7 87，97 2 8 98 1 合計 45 ]

模式一的分類依據(jù)是“十位數(shù)字相同歸為同一類”，模式二的分類依據(jù)是“個位數(shù)字相同歸為同一類”。所有的排序都依據(jù)“從小到大”。可以概括地說，“分類與排序”是對“整齊模式”的建構。模式雖然不同，但“整齊”的效果是一致的。由此就可以得到一種思考問題的方法，不妨叫作“變亂為齊”。

三、 局部與整體

先看一個例子：如圖2， ABC是任意一個三角形，D是AB邊上的中點，E是BC邊上的中點。連接CD和AE兩條線段，將三角形ABC分為了四個部分。如果假設三角形ABC的面積為1，那么這四個部分的面積分別是多少？

把整個三角形ABC看作一個整體，那么三角形ACO、三角形ADO、三角形CEO和四邊形BEOD就是相對于這一整體的四個局部。學習數(shù)學過程中習慣的問題是已知局部求整體，而這個問題恰好是反過來，是已知整體求局部的問題。

在一般情況下，局部一旦確定，則整體也就隨之確定。反過來，整體確定，局部卻未必確定。這個問題恰恰就是“已知整體求局部”，因此問題的思維障礙就在于這種“不確定”。產生障礙的基本矛盾自然就是“整體”與“局部”的對立。解決問題的關鍵就在于統(tǒng)一整體與局部之間的矛盾，這種統(tǒng)一依賴于二者之間的數(shù)量關系。

所謂“不確定”體現(xiàn)的是一種動態(tài)，而制約這種動態(tài)的基本元素就是D點和E點的位置，這兩個點的位置一旦確定，這種動態(tài)就轉變?yōu)殪o態(tài)了。問題的已知信息告訴我們，D點和E點分別是所在邊上的中點，從而四個局部之間的關系也就確定了，要想發(fā)現(xiàn)局部與整體之間的數(shù)量關系，應該從發(fā)現(xiàn)局部與局部之間的關系入手。

首先不難看出，整個三角形圖形中有4個面積為三角形ABC面積[12]的三角形，分別是三角形ACD、CDB、ACE和AEB。由于三角形AEB和CDB的面積都是[12]，同時去掉它們的公共部分ODBE就可以知道三角形OCE和AOD的面積相等。這時的關鍵問題在于建立四邊形ODBE與這兩個三角形之間的關系，可以連接OB畫出一條輔助線，見圖3。

利用 “等底等高的三角形面積相等”這一結論，立刻知道三角形AOD和OBD面積相等，三角形OCE和OEB面積相等。又由于三角形OCE和AOD面積相等，所以AOD、OBD、OEB和OCE這4個三角形面積相等，而且其中3個三角形的面積之和為原三角形ABC的[12]，因此現(xiàn)在就可以求出三角形AOD和OCE的面積分別為：

[12÷3=16]

四邊形ODBE的面積為：

[16×2=3]

進而就可以求出三角形ACO的面積為：

1[-16×2-13=13]

至此四個部分的面積就都求出來了。

關于“局部”與“整體”之間的矛盾，在不同領域可以有不同的意義。這個問題中反映出來的實際上是“動態(tài)”與“靜態(tài)”之間的對立統(tǒng)一。

四、 動態(tài)與靜態(tài)

日常生活中開玩笑的時候，形容一個長著“八字眉”的人的眉毛就像“8點20分”一樣（見圖4）。

這是非常形象的描述，但仔細想一想會發(fā)現(xiàn)，這個形容并不精確。事實上，用鐘表上的時針和分針描述“八字眉”時，時針與分針應該處于對稱位置（見圖5）。

也就是說，兩針應該以鐘表上“6”和“12”兩點的連線為對稱軸。而“8點20分”時分針指向“4”，時針指向“8”與“9”之間距“8”的三分之一處，這時顯然兩針并不處于對稱位置（見圖6）。

日常語言描述“八字眉”的不精確，促使人產生了解“八字眉”到底應該是8點多少分的欲望。因此“問題”就產生了。用數(shù)學的語言敘述這個問題就是：8點多少分時，時針與分針關于“6”與“12”的連線對稱？

鐘表是描述時間的工具，時間的“動態(tài)”是永恒的。鐘表上所謂“八字眉”的狀態(tài)是一種“靜態(tài)”。而這種靜態(tài)的時刻，直觀上又不能準確地確定。因此需要把 “靜態(tài)”融入到“動態(tài)”之中，實現(xiàn)二者的統(tǒng)一。

時間的動態(tài)，在鐘表上反映出來的是指針的運動。所謂“八字眉”的靜態(tài)實質上就是指針運動過程中的一個“瞬間”。時間的動態(tài)無始無終，因此需要截取一個時間段，也就是規(guī)定兩個“瞬間”分別作為時間段的“起點”和“終點”。當然，這個時間段的截取有一定的隨意性，需要考慮怎樣截取有益于問題的解決。

如果把8點整作為“起點”，把“八字眉”的時刻作為“終點”，那么問題就變成了從起點到終點經過了多少分鐘？這樣就把時間的“動態(tài)”與“八字眉”的“靜態(tài)”有機地聯(lián)系起來了。

為了借助“行程問題”的解決方法，就需要“路程”和“速度”這樣的量，前提是需要有“路程單位”。比如，可以規(guī)定時針1小時轉過的1格為1個路程單位，這樣，時針的轉動速度就是每分鐘[160]格，分針的轉動速度是每分鐘[15]格。

直觀上不難看出，“八字眉”的時刻應該是8點15分至8點20分之間。所謂時針與分針處于對稱位置，實際上就是8點多鐘的某一時刻，時針、分針所指向的位置與鐘表上數(shù)字“6”所在位置的距離相等。

從8點整開始想，時針指向“8”，分針指向“12”，假設從這時到兩針所指位置與數(shù)字“6”的位置距離相等用了x分鐘，分別將時針與分針過x分鐘后與數(shù)字“6”的距離表示出來，就可以列出如下方程：

2+[x60]=6-[x5]

解方程得：x=[18613]

因為兩針與“6”的距離相等，也就是與“12”的位置距離相等，所以還可以分別將兩針經過x分鐘后與“12”的距離以列方程的形式表示出來：

4-[x60=][x5]

同樣可以解得：x=[18613]

最后需要說明，雖然通過識別問題的障礙進行矛盾分析是發(fā)現(xiàn)解決問題方法的有效途徑，但由于問題的障礙具有相對性，也即面對同樣的問題或不同的問題解決者，問題的障礙可能是不同的，所以問題解決的矛盾分析具有相當?shù)膹碗s性。

（首都師范大學初等教育學院 100048）