往復壓縮機氣閥故障混合診斷方法研究

張思陽， 徐敏強， 李永波， 趙海洋， 王日新

(1.哈爾濱工業大學 航天學院，哈爾濱　150001； 2.哈爾濱石化公司，哈爾濱　150056)

往復壓縮機氣閥故障混合診斷方法研究

張思陽1,2， 徐敏強1， 李永波1， 趙海洋1， 王日新1

(1.哈爾濱工業大學 航天學院，哈爾濱150001； 2.哈爾濱石化公司，哈爾濱150056)

由于往復壓縮機氣閥振動信號呈現強非線性和非平穩性特點，目前應用較好的三次樣條EEMD(S-EEMD)方法仍然存在模態混疊及包絡不準確問題。針對此情況提出一種基于四次Hermite插值EEMD(QH-EEMD)與功率譜熵(PSE)相結合的分析方法。結合四次Hermite插值保形性、可調性與EEMD提高信號在不同分解尺度上連續性的優點改善插值曲線的逼近精度，減少模態混疊，通過對振動信號進行分解，得到IMF分量。通過與S-EEMD-PSE(S-EEMD結合PSE)算法、QH-EEMD-SE(S-EEMD結合樣本熵)算法比較，驗證了QH-EEMD-PSE(QH-EEMD結合PSE)方法的優越性。以往復壓縮機常見故障為研究對象，基于QH-EEMD-PSE方法提取故障特征實現了常見故障的準確診斷。

EEMD；功率譜熵；往復壓縮機；故障診斷

往復壓縮機在石油石化行業中應用廣泛。其中氣閥承擔著輸送介質的重要任務，需要頻繁開啟，易出現故障，因此分析氣閥故障信息對機組安全運行非常重要。由于氣閥閥片薄板結構及周期性沖擊力造成氣閥高頻振動，產生信號沖擊和調制現象。往復壓縮機的多分量調幅調頻振動信號包含氣閥故障信息，對振動信號有效分析可以診斷氣閥故障。然而往復壓縮機振源復雜，干擾因素眾多，機組故障點被隱藏于干擾因素當中，造成往復壓縮機故障診斷困難。

故障分析方法[1]包括時域法、頻域法、時頻法。時域法無法定位往復壓縮機故障部件，頻域法易產生邊頻現象且無法確定故障時間。為克服上述缺點，提出時頻法。典型時頻法包括Hilbert變換、小波變換[2]、二代小波變換[3]、EMD[4]、EEMD[5]等方法。小波及其衍生方法能夠分析頻域成分隨時間變化情況，但其基函數選取困難，無法根據信號特性變化自動調節。針對往復壓縮機信號時變特點，EMD法能自適應地進行時頻調節，實現對信號時變特性分析，但易產生模態混疊、邊頻等缺陷。EEMD方法部分改善了模態混疊、邊頻缺點，在離心式壓縮機故障診斷領域中得到廣泛應用。但三次樣條EEMD法對往復壓縮機的強非線性、非平穩性信號仍存在過包絡或欠包絡情況，而產生模態混疊情況，造成分析精度過低，不能有效識別往復壓縮機故障。為了提高包絡精度及克服模態混疊等缺陷。本文利用Hermite插值[6]保形性對信號進行包絡線擬合，有效避免過包絡及欠包絡情況，提高信號分解準確性。結合EEMD和Hermite插值各自優點，提出利用四次Hermite插值的EEMD方法(簡稱QH-EEMD)對振動信號進行分析。并應用功率譜熵[7](簡稱PSE)對IMF主分量計算結構信息。與樣本熵對比分析，驗證功率譜熵對正常、故障狀態振動信號分解的優越性。四次Hermite插值相對于三次樣條插值能更好地逼近被插值函數，相比于三次Hermite插值及有理Hermite插值具有更佳的調控性和逼近效果。綜合以上分析，提出基于四次Hermite插值EEMD聯合PSE進行往復壓縮機特征識別、故障診斷的方法。

1QH-EEMD與PSE特征提取法

1.1QH-EEMD方法

三次樣條插值EEMD(簡稱S-EEMD)方法成功應用于離心壓縮機故障部件診斷[8]。通過多次疊加白噪聲及經驗模式分解，利用白噪聲頻率統計均勻性，保證信號連續性，將信號從高頻至低頻分解為有限個反映不同振動頻段的本征模態函數(IMF)和余項的經驗模態分解方法。

本征模態函數需要滿足條件：序列中，極值點數與過0點數必須相等或者最多相差一個；在任意時間點上，由信號局部極大值確定的上包絡線和由局部極小值確定的下包絡線均值為0。對強非線性和非平穩性信號EEMD方法分析，發現仍存在過包絡及欠包絡情況。相比三次樣條插值，本文提出采用四次Hermite插值函數對強非線性、非平穩性信號進行包絡。Hermite插值函數滿足插值多項式在節點處與被插值函數相等，插值多項式導數值與被插值函數導數值相等，即擬合點與被插值點相切。通過引入形狀參數，利用對稱點作為包絡點，考慮相關干擾因素經調節參數值來調整插值曲線形狀，并隨著原始曲線形狀自主調節包絡曲線。構造四次Hermite插值。

對0≤t≤1，應用四次Hermite基函數作為插值基函數[9]：

(1)

式(1)中λi表示形狀參數，為任意實數。選取一個序列數據，任選兩個插值取樣點xi,xi+1，其插值函數：

(2)

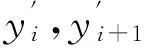
(3)

且存在如下關系：

Fi(t)+Fi+1(t)=1,Gi(t)=-Gi+1(1-t)

(4)

研究證明[9]四次Hermite插值函數具有自動可調性，比三次樣條具有更好包絡精確性和擬合逼近精度，更精確擬合信號上、下包絡線。結合EEMD，對于給定原始離散信號x(n)，同樣在信號序列中多次加入等長度正態高斯白噪聲序列，設第i次加入噪聲信號xi(n)，加入高斯白噪聲標準差為ε。利用QH擬合信號上、下包絡線，對包絡極值求平均，得到均值序列m1(n)。從xi(n)中去除均值序列m1(n)得到待檢測信號，判斷待檢測信號是否為本征模態函數。如果非本征模態函數，需要以xi(n)-m1(n)為新處理信號重復包絡、均值操作，經過多次循環得到本征模態函數。重復以上步驟，繼續計算剩余信號，多次循環依次得到IMF1、IMF2…IMFm。m為分解層數，n為采樣點數。

根據文獻[6]，通常加入噪聲次數N為100的倍數，ε為擬處理數據幅值0.2倍以上。經過數據分析，發現對強非線性、非平穩性信號，需進一步提高N、ε值，當N取500，ε為0.25時，通過標準誤差分析，數據計算結果穩定。

1.2功率譜熵(PSE)方法

信息熵用來描述概率系統平均不確定程度。如果系統中各事件出現概率相等，則該系統信息熵具有最大值。具體推導如下：

如果某系統S內有多個事件，設S={S1,S2,…,Sn}，事件概率分布為：P={P1,P2,…,Pn}，相應信息熵為：

(5)

若概率系統為連續系統，設其概率分布為p(x)，則信息熵為：

(6)

式中：x∈[x0,x1]

根據信息熵原理，求振動模態本征模態函數IMF各分量功率譜熵。設IMF為一向量序列，設某一分量為x(i)，定義功率譜：

(7)

相應功率譜熵函數：

(8)

功率譜熵(PSE)：

(9)

PSE表征了振動信號能量譜型結構信息。在正常運行狀態下，振動信號能量分布均勻，功率譜熵值最大，當出現故障時，多數情況下會引起振動信號內部能量集中，造成能量分布混亂度降低，反應到整體或局部振動譜型變化，其相應功率譜熵值減小。

對于振動信號的時間序列，樣本熵[10]為：

(10)

式中：m表示組成時間序列向量的維數值，r表示樣本熵(SE)距離閾值，n表示數據總數。根據數據特點，取m=2，r=0.25。

1.3方法結合分析

對典型故障分析，直接應用QH-EEMD方法得到多層次IMF數據，通過IMF數據分析設備問題。此方法對離心機故障識別清晰。對于往復壓縮機采用QH-EEMD方法可以識別設備運行狀態，但往復壓縮機具有振源、振因復雜、故障類型模糊、振動信號強非線性、非平穩性特點，增加了診斷人員確定故障類型難度。因此考慮對QH-EEMD分解分量進一步分析，利用功率譜熵對IMF數據進行計算，量化故障分布信息。此處采用功率譜熵對QH-EEMD分解后IMF分量計算，對各頻段能量混亂度進行度量，不同于計算原始振動信號功率譜熵的方法。

往復壓縮機振動信號經過QH-EEMD分解后形成了不同頻段的分頻振動信號，即IMF分量。分頻振動信號實際上由一個包絡信號和一個純調頻信號調制而成，即：

S=Senvelop*Sfrequency

(11)

進一步建立功率譜、功率譜熵函數，利用功率譜熵對各分頻振動信號自身混亂度進行量化處理。通過計算主要IMF分量功率譜熵的不同情況，分析往復壓縮機故障。

1.4算法與流程

給定信號x(n)，用QH-EEMD結合PSE方法對信號分析，故障診斷主要步驟為:

(1) 用QH-EEMD方法分別對往復壓縮機不同狀態氣閥的振動信號進行分解，每種狀態得到一系列IMF分量；

(2) 利用功率譜熵函數計算各狀態主要IMF分量功率譜熵值。

具體方法如流程圖1所示。

圖1　QH-EEMD與功率譜熵結合法分析流程Fig.1 QH-EEMD analysis program combined with PSE

2氣閥故障診斷

氣閥通過閥片與閥座配合實現氣體密封，隨氣缸內壓力和彈簧力變化自動周期地開啟與關閉，實現氣體輸送。為了說明氣閥基本結構和工作原理，采用Solidworks繪制氣閥基本結構示意圖，如圖2所示。

圖2　氣閥結構示意圖Fig.2 Diagram of valve structure

往復壓縮機經歷一個工作循環時，吸氣閥、排氣閥均需啟閉一次。由于閥片運動速度較大，撞擊能量較高，反映在振動曲線上幅值較大，出現振動沖擊現象。氣閥通常易產生閥片斷裂、彈簧失效、閥片缺口等故障。本文針對2D12-70型往復壓縮機進行故障設置，采集振動數據分析。機組曲軸轉速496 r/min，采樣點數為1 024點，采樣頻率為20 K，具體故障設置情況見表1所示。

表1　試驗氣閥故障設置

根據信號采樣頻率及轉速，參考壓力信號及鍵相信號，選取多周期數據優化分析獲得整周期數據如圖3所示。

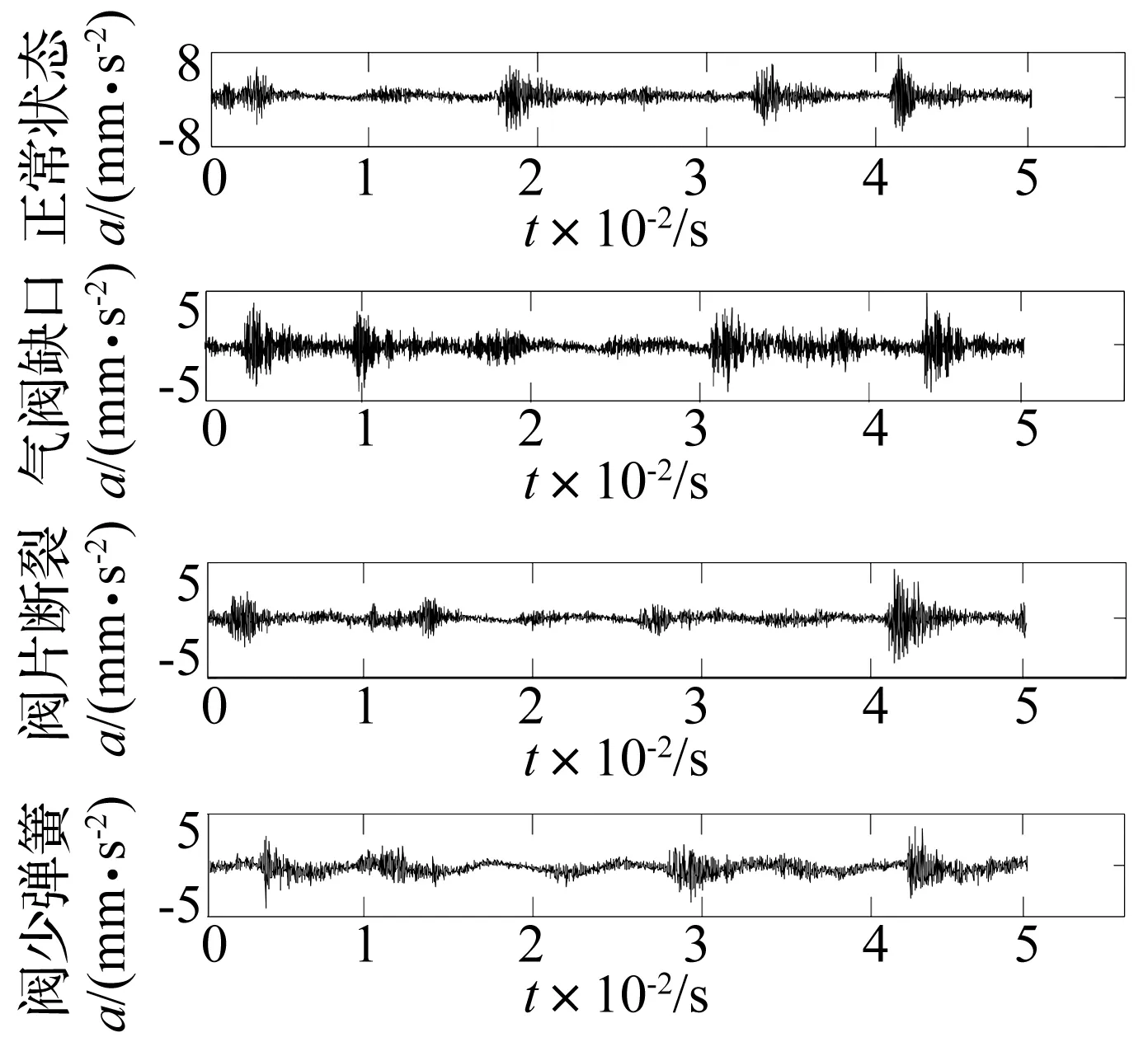
圖3　四種狀態的原始振動波形Fig.3 Four kinds state of primary vibration waves

圖3為機組正常運行，機組二級氣缸側排氣閥閥片斷裂、排氣閥缺口、排氣閥少彈簧四種狀態的原始振動波形。從原始振動波形圖上難以區分正常狀態及不同故障狀態，不能有效提取故障特征，需進一步分析。

2.1QH-EEMD方法分析

(1) 方法對比圖形分析

分別利用基于三次樣條插值EEMD分解方法(以下簡稱S-EEMD)、基于四次Hermite插值EEMD分解方法(以下簡稱QH-EEMD)對正常振動信號分解及分析。

分別采用QH-EEMD方法及S-EEMD方法對往復壓縮機振動信號分解，對比分析QH-EEMD方法優越性。引入相鄰極值點的對稱點來優選形狀參數，進行包絡線自動尋優，通過對各取樣點間線段局部尋優實現對整體包絡線的優化提高了信號的局部特征的描述，得到更好上下包絡線，減小包絡誤差，從而減少分解分量的模態混疊現象，使信號分解結果更加準確。

S-EEMD與QH-EEMD方法分解振動信號各得到11組IMF分量及一組余量。通過相關系數法[11]，選取反映機組主要信息的前四級分量于圖4、5中對比分析。圖4為S-EEMD分解得到IMF前四級分量；圖5為QH-EEMD分解得到IMF前四級分量。

圖4　正常狀態的S-EEMD分解Fig.4 S-EEMD decomposition of normal state

圖5　正常狀態的QH-EEMD分解Fig.5 QH-EEMD decomposition of normal state

從分解結果對比，S-EEMD方法數據處理結果存在過包絡、欠包絡及模態混疊情況，具體如圖4所示。IMF2、IMF4中存在著模態混疊的情況。而QH-EEMD方法模態識別清晰、精度高，避免了模態混疊等情況，具體如圖5所示。

進一步分析QH-EEMD 分量消除模態混疊的優越性。模態混疊產生的原因[12]：模態混疊主要表現為未能有效識別與分離相近的二類或幾類不同性質的模態，由于包絡不準確影響了插值曲線未能有效逼近被插值信號[13]，因此造成頻率混疊現象。由于往復壓縮機的信號呈現出強非線性和非平穩性，S-EEMD方法的包絡曲線形狀無法自動調節，因此包絡曲線對信號的跟隨性不好，包絡曲線未能真實反映出被插值曲線的時頻特性，造成過包絡、欠包絡及模態混疊的情況。為了能夠有效逼近被插值信號，要求插值曲線與被插值曲線無限接近且插值曲線能夠及時跟隨被插值曲線的頻率及形狀變化來調整自身的包絡線形狀。

由于四次Hermite插值函數相對于三次樣條函數甚至于三次Hermite插值函數具有自動調節特性并且吸收了極值點的對稱點作為插值點，提高了信號的跟隨性和包絡曲線的對稱性。

為了進一步說明四次Hermite插值函數的優越性，將一段振動信號分別采用三次樣條與四次Hermite插值方法得到的包絡線對比分析，具體如圖6所示。

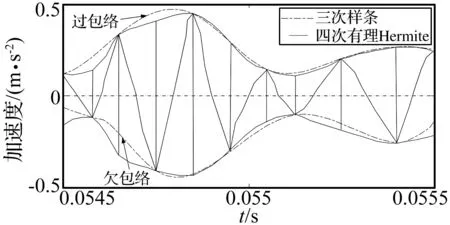
圖6　三次樣條與四次有理Hermite包絡情況比較Fig.6 Compare of envelop of cubic-sample and quartic rational Hermite

對圖6兩種插值曲線進行對比，發現四次Hermite插值曲線有效避免了三次樣條插值曲線產生的過包絡和欠包絡現象，因此獲得了較好的分解效果。

(2) 指標評價

采用均值正交指標(Index of Average Orthogonality, IAO)以及能量守恒指標(Index of Energy Conservation, IEC)對不同插值方法分解結果進行評價。由于包絡線的擬合性能越好，各分頻信號越接近于純調頻信號，達到純調頻信號標準所需包絡解調的次數越少。因此，可以從IMF分量迭代次數評價包絡方法精度。另外，EEMD分解結果中各個IMF分量都與理想情況下的完全正交(此時Iao=0)存在一定的差值，因此各個IMF分量之間的正交指標可作為定量評價分解結果的標準。采用所有任意兩個IMF分量正交性的均值Iao對不同方法進行評價。另外，信號分解前后應該滿足能量守恒定律，各IMF分量若完全正交可得能量守恒指標Iec=1，該指標從能量角度對分解結果進行評價。均值正交指標和能量守恒指標為：

(12)

式中：x(t)為原始信號，Imfj(t)為分解得到的各個IMF分量，Rn(t)為殘余分量。

三次樣條插值與四次Hermite(QH)插值三個IMF分量的迭代次數、均值正交指標以及能量守恒指標如表2所示。由表2可知，三次樣條插值法因出現過包絡與欠包絡現象，所以迭代次數較多，而四次Hermite插值法明顯優于三次樣條Hermite插值法，迭代次數較少。在正交性和能量守恒指標方面，四次Hermite插值法明顯優于三次樣條插值法，說明了四次Hermite插值法對非平穩性號的優良擬合逼近性能以及選擇極值對稱點作為包絡控制點的有效性。

表2　各方法分解結果性能指標

(3) 故障信號分解

對前面設置的三種故障采集振動信號，經數據處理后采用QH-EEMD方法分解，取前四級分量分析。如圖7～9所示，分別對應排氣閥閥片缺口、排氣閥閥片斷裂及排氣閥少彈簧故障振動信號前四級IMF分量。采用QH-EEMD方法對各狀態進行分解得到各自分量。由圖7～9發現三種故障對應不同波形。

排氣閥閥片缺口時由于吸氣階段存在漏氣情況，吸氣閥打開波形不明顯；閥片斷裂時存在吸氣階段氣流不穩定情況，吸氣閥出現多次打開情況；氣閥少彈簧時高頻振動較弱，低頻擾動明顯，說明QH-EEMD分解方法能夠對不同故障進行有效區分。

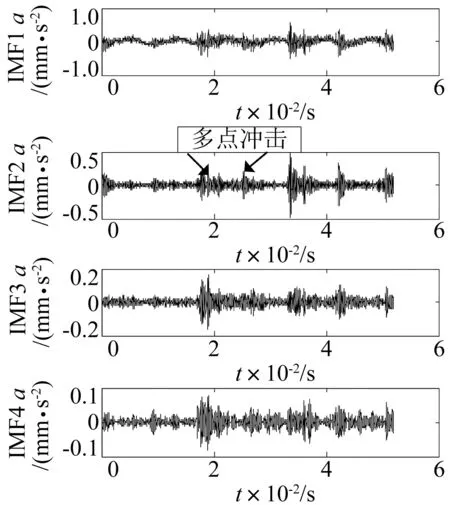
圖8　氣閥閥片斷裂故障的QH-EEMD分解Fig.8 QH-EEMD decomposition of discharge valve crack fault

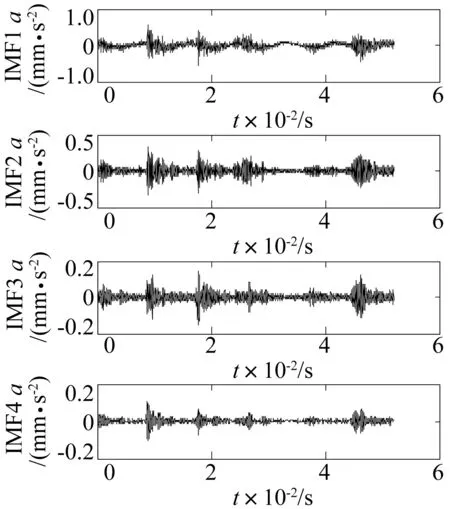
圖9　氣閥少彈簧故障的QH-EEMD分解Fig.9 QH-EEMD decomposition of discharge valve less spring fault

QH-EEMD方法將故障信號精確分解到不同頻段避免了模態混疊、包絡不準確等情況。不同故障從圖7～9上比較存在明顯區別，但通過圖形分析特征值不夠明顯，進一步采用功率譜熵方法提取不同頻段的正常及故障狀態特征值，進行故障識別。

2.2功率譜熵的特征提取

通過QH-EEMD方法對正常狀態及故障狀態振動數據分解獲得IMF分量，計算QH-EEMD前四個IMF分量的樣本熵、功率譜熵及三次樣條插值的EEMD(簡稱S-EEMD)功率譜熵。得到三組四種狀態的IMF1～4樣本熵、功率譜熵及標準偏差數據如圖10～12所示。

圖10　QH樣本熵分析圖Fig.10 SE analysis diagram of QH-EEMD

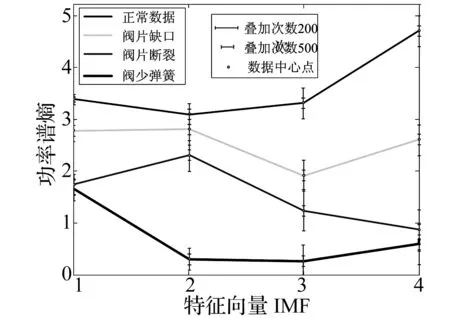
圖11　QH功率譜熵分析圖Fig.11 PSE analysis diagram of QH-EEMD

圖12　基于三次樣條插值功率譜熵分析圖Fig.12 PSE analysis diagram of S-EEMD

經過采樣誤差分析[14]，當數據量、疊加次數較少時，計算結果波動性較大，不同狀態存在數據重疊情況，無法有效識別。隨著數據量提高到500周期、疊加次數達500時，數據穩定，誤差在0.1以內。三種熵分析方法的不同數據量對比均表明功率譜熵識別效果優于樣本熵，四次Hermite插值優于三次樣條插值。三次插值功率譜熵及樣本熵狀態間存在部分疊加情況，從功率譜熵分析圖上識別，正常狀態與故障狀態之間IMF1～IMF4功率譜熵區分明顯，表明功率譜熵故障分類方法的有效性。

對功率譜熵圖形進行拓撲分析。由于正常狀態能量混亂度最高，其IMF1～IMF4功率譜熵值最大且波形為整體上升趨勢，和各故障狀態有明顯區別；少彈簧故障能量混亂度最低，整體線型較平緩，其IMF1～IMF4功率譜熵值最小；閥片缺口故障氣量變化弱于閥片斷裂故障，對能量影響稍小，能量混亂度高于閥片斷裂情況，故其故障功率譜熵值大于閥片斷裂故障。通過計算正常及各故障數據功率譜熵值，通過不同頻段功率譜熵值比較及同一狀態不同功率譜熵值線型分析，有效地識別氣閥各種運行狀態。

3結論

針對往復壓縮機氣閥振動信號進行分析，提出QH-EEMD和PSE相結合方法。先通過QH-EEMD對振動信號分解，得到不同頻段IMF值，再通過相關系數自動提取包含故障信息較多的前四級分量進行功率譜熵計算及分析，根據計算結果識別故障。通過對往復壓縮機故障診斷實例分析，驗證該方法的有效性。

(1) QH-EEMD方法相比于傳統S-EEMD方法故障識別能力強，通過相關指標評價，確認該方法模態識別清晰，識別精度高，有效避免模態混疊。對往復壓縮機振動信號分析驗證QH-EEMD法處理強非平穩、非線性振動信號的可靠性。

(2) 對QH-EEMD分解的IMF分量計算功率譜熵，相比于樣本熵，計算精度更高。通過功率譜熵計算發現正常信號功率譜熵值較大，而故障狀態下各功率譜熵值均較正常狀態下功率譜熵值有所減少，且相互之間存在明顯區別。

[ 1 ] Jardine A K S,Lin D,Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance [J]. Mechanical Systems and Signal Processing,2006,20(7):1483-1510.

[ 2 ] 袁小宏,屈梁生.小波分析及其在壓縮機氣閥故障檢測中的應用研究[J].振動工程學報,1999,12(3):410-415.

YUAN Xiao-hong, QU Liang-sheng. Wavelet analysis and its application to valve fault detection of reciprocating compressor [J]. Journal of Vibration Engineering,1999,12(3):410-415.

[ 3 ] 姜洪開,竇丹丹,何正嘉.基于自適應第二代小波的超聲回波信號特征識別[J].西北工業大學學報,2011,29(1):93-96.JIANG Hong-kai, DOU Dan-dan, HE Zheng-jia. A new method for identifying ultrasonic echo signal features using adaptive second generation wavelet[J]. Journal of Northwestern Poly-technical University,2011,29(1):93-96.

[ 4 ] Li Yu-jun, Tse P W, Yang Xin, et al. EMD-based fault diagnosis for abnormal clearance between contacting components in a diesel engine [J]. Mechanical Systems and Signal Processing,2010,24:193-210.

[ 5 ] Wu Zhao-hua, Huang N E.Ensemble empirical mode decomposition: A noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis,2009,1(1):1-41.

[ 6 ] Kopsinis Y, McLaughlin S. Investigation and performance enhancement of the empirical mode decomposition method based on a heuristic search optimization approach[J]. IEEE Transactions on Signal Processing,2008,56 (1):1-13.

[ 7 ] 王凱明,鐘寧,周海燕.基于改進功率譜熵的抑郁癥腦電信號活躍性研究[J].物理學報,2014,63(17):178701:1-8.

WANG Kai-ming, ZHONG Ning,ZHOU Hai-yan. Activity analysis of depression electroencephalogram based on modified power spectral entropy[J]. Acta Phys. Sin. 2014,63(17):178701:1-8.

[ 8 ] Jiang Hong-kai, Li Cheng-liang, Li Hua-xing.An improved EEMD with multi wavelet packet for rotating machinery multi-fault diagnosis Mechanical [J] Systems and Signal Processing,2013(36):225-239.

[ 9 ] 李軍成,劉純英,楊煉. 帶參數的四次Hermite 插值樣條[J].計算機應用.2012,32(7): 1868-1870.

LI Jun-cheng, LIU Chun-ying, YANG Lian. Quartic Hermite interpolating splines with parameters [J]. Journal of Computer Applications, 2012,32(7): 1868-1870.

[10] 張思陽,徐敏強,王日新，等. EMD與樣本熵在往復壓縮機氣閥故障診斷中的應用[J].哈爾濱工程大學學報,2014,35(6):696-700.

ZHANG Si-yang，XU Min-qiang, WANG Ri-xin,et al. Application of EMD and SampEn to the fault diagnosis of reciprocating compressor valves [J]. Journal of Harbin Engineering University, 2014,35(6):696-700.

[11] 陳成法,李樹珉,張建生，等.基于EEMD及敏感IMF的再制造發動機振動模式研究[J].振動與沖擊,2014,33(2):117-121.

CHEN Cheng-fa, LI Shu-min,ZHANG Jian-sheng, et al. Vibration mode of remanufactured engine based on EEMD and sensitive IMF[J]. Journal Vibration and Shock,2014,33(2):117-121.

[12] 王婷.EMD算法研究及其在信號去噪中的應用[D].哈爾濱:哈爾濱工程大學.201006.

[13] 謝進,檀結慶,李聲鋒.有理三次Hermite插值樣條及其逼近性質[J].工程數學學報,2011,28(3):385-392.

XIE Jin, TAN Jie-qing, LI Sheng-feng.Rational cubic Hermite interpolating spline and its approximation properties[J].Chinese Journal of Engineering Mathematics,2011,28(3):385-392.

[14] Wu S D, Wu C W, Lin S G,et al. Time series analysis using composite multiscale entropy [J]. Entropy,2013(15):1069-1084.

Valve fault diagnosis of a reciprocating compressor based on hybrid method

ZHANG Si-yang1,2, XU Min-qiang1, LI Yong-bo1, ZHAO Hai-yang1, WANG Ri-xin1

(1. Astronautics Institute, Harbin Institute of Technology, Harbin 150001, China;2. Petrochina Harbin Petrochemical Company, Harbin 150056, China)

Due to strong nonlinear and non-stationary characteristics of a reciprocating compressor’s valve vibration signals, the cubic spline interpolation EEMD (S-EEMD) method well utilized still has shortages of mode mixing and envelop inaccurate. Aiming at the above mentioned problems, the combined analysis method of EEMD based on the quartic Hermite interpolation (QH-EEMD) and the power spectral entropy (PSE) was proposed. The original signals were decomposed into a set of IMF components using the quartic Hermite method with advantages of shape-preserving and adjustability and the EEMD method promoting signals’ continuity in different decomposing scale to improve the approximation accuracy of the interpolation curve and to decrease mode mixing. The advantages of the QH-EEMD with PSE (QH-EEMD with PSE) analysis method were verified comparing with those of the S-EEMD-PSE (S-EEMD with PSE) method and the QH-EEMD-SE(QH-EEMD with sample entropy) method. Taking common faults of a reciprocating compressor as the study objects, feature vectors of faults were extracted based on the QH-EEMD-PSE method and the faults were diagnosed accurately.

EEMD; power spectral entropy (PSE); reciprocating compressor; fault diagnosis

10.13465/j.cnki.jvs.2016.11.026

國家自然科學基金資助項目(10772061)

2015-04-09修改稿收到日期：2015-06-14

張思陽 男，高級工程師,博士生，1971年4月生

徐敏強 男，教授，博士生導師，1960年9月生

E-mail:xumq@hit.edu.cn

TH17；TH4

A