高維強非線性隔振系統諧波及分岔分析

何其偉, 俞　翔, 毛為民

(1 海軍工程大學 科研部,武漢　430033； 2 浙江凱靈船廠,浙江 舟山　316000)

高維強非線性隔振系統諧波及分岔分析

何其偉1, 俞翔1, 毛為民2

(1 海軍工程大學 科研部,武漢430033； 2 浙江凱靈船廠,浙江 舟山316000)

從次諧波級聯角度，利用諧波平衡法與跟蹤延拓算法得到了高維強非線性隔振系統各級次諧波的幅頻特性曲線，分析了次諧波的穩定性，研究了兩條分岔道路，得到了典型的倍周期分岔值，以此估計了混沌參數區域，與數值計算結果吻合較好。

非線性；次諧波；分岔；混沌

非線性系統中存在三種有界定常運動：周期運動、準周期運動與混沌運動，這三種形式的運動均有可能出現在強非線性隔振系統中，而周期運動是最普遍、在參數空間中占據最大區域的一種運動形式，深入研究強非線性隔振系統的周期運動對于了解其動力學特性并進行非線性控制研究具有重要的意義[1-3]。周期運動中，次諧波扮演著非常活躍的角色，新次諧波的出現往往意味著系統周期的改變，即分岔的發生，這也是次諧波分析相對而言更為重要的原因[4-5]。李天巖等[6]的著名文章“周期3意味著混沌”更深刻揭示了次諧波在從有序到混沌的演化過程中所起的重要作用。

分析強非線性隔振系統的諧波特性及其分岔行為，不僅可利用其豐富的動力學特性，為設計具有高靜態剛度、低動態剛度特性的新型強非線性隔振器提供理論依據[7]，還可利用次諧波級聯預測出的混沌參數區域來對非線性隔振系統實施混沌反控制，從而改變系統振動的線譜結構，提高水下航行器的隱聲性能[8]。

本文首先介紹了次諧波級聯的有關思想，建立高維非線性隔振系統動力學方程，隨后應用諧波平衡法對各次諧波的幅頻特性與穩定性進行分析，對T→…→2nT→Chaos以及倍周期分岔序列進行了研究，通過分析次諧波級聯、次諧共振、倍周期分岔、鞍結分岔等建立起高維強非線性隔振系統各次諧波的整體圖像。本文采用的方法為跟蹤延拓算法，可以利用了符號計算軟件強大的符號計算功能得到較高截斷階數的諧波平衡解表達式，而免去了繁瑣的推導過程。

1次諧波級聯

非線性系統中次諧波的存在形式與系統非線性形式有關，Lukomsky與Gandzha在文獻[9]中對如下的振動方程：

(1)

存在的次諧波形式進行了詳細討論，并給出了圖1。圖1中同心圓的中心點S1表示零級的次諧波，周期為T，其中T為激勵力周期，即零級次諧波包括基諧波響應與超諧波響應。零級次諧波通過周期2、3、5等質數倍增產生第一個圓周上的第1級次諧波，以Sm示，它們是最基本的次諧波成分，其周期為mT，其中m為質數(m=2,3,5,7,…)。第1級次諧波也可再一次產生周期質數倍增，從而產生第2個同心圓周上的第2級次諧波Sm×n，其中n也為質數(n=2,3,5,7,…)。與此類似，可以得到l級次諧波成分，其周期為NlT，Nl為l個質數的乘積。這樣，非線性系統中所有可能的次諧波成分，均可以通過圖1得出其可能產生的路徑，這樣的路徑并不唯一，例如周期為6T的次諧波S6既可以通過S1→S2→S6的過程得到，也可以通過S1→S3→S6得到。對于特定的非線性系統來說，并非圖中所示的所有次諧波成分均會出現，也并非通向某個次諧波的每條路徑都會在該非線性系統中實現，這些都與系統非線性項的具體表達形式有關。

本文將采用上述有關次諧波級聯的思想，按照第0、1、2級的順序來求解強非線性隔振系統中可能存在的次諧波成分，并對倍周期分岔進入混沌的典型道路S1→S2→S4→…→S2j→Chaos進行分析。

圖1　次諧波級聯示意圖[9]Fig.1 Cascades of subharmonic states [7]

2諧波分析

2.1動力學方程

考慮豎直方向振動的雙層隔振系統，且系統只受簡諧激勵。因文獻[10]對該系統的運動方程進行了推導，本文不再詳細推導。消除重力項并無量綱化后，其運動方程可以寫為：

(2)

式中:f為激勵力幅值，ω為激勵頻率。

2.2諧波平衡法

在下文中，用j表示次諧波級數，本文僅考慮S1→S2→S4→…→S2j→Chaos這條倍周期分岔道路，因此對于式(2)，它的諧波可以寫成如下截斷傅里葉級數形式：

bi,2-jnsin(2-jnωt))i=1,2;j=0,1,2,…

(3)

bi,2-jncos(2-jnωt))

bi,2-jnsin(2-jnωt))

i=1,2;j=0,1,2,…

(4)

(5)

其中：

(6)

式中x1(t)由式(3)表示。將式(3)、(4)代入式(2)第二式，令各階諧波系數等于零。由于式(2)的第二式為線性系統，因而x2(t)的各諧波系數均可以由x1(t)相同階諧波系數線性表示，這也是為何消除重力項而將剛度耦合變換為慣性耦合的原因，這樣可以得到：

c2,0=0,a2,1=Q1a1,1+P1b1,1-Q1f/ω2,

b2,1=-P1a1,1+Q1b1,1+P1f/ω2,

a2,2-jn=Q2-jna1,2-jn+P2-jnb1,2-jn,

b2,2-jn=-P2-jna1,2-jn+Q2-jnb1,2-jn,

(7)

其中：

(8)

將式(3)～(8)代入式(2)第一式，令各階諧波系數等于零，可以得到一非線性代數方程組，通過求解該方程組可以得到式(3)中x1(t)各諧波的傅里葉系數。當然，要解析求解該非線性方程組相當困難，可以采用定常解的跟蹤延拓算法求得，有關跟蹤延拓算法詳見文獻[11-12]。求得各諧波傅里葉系數后，可以求得各諧波的幅值：

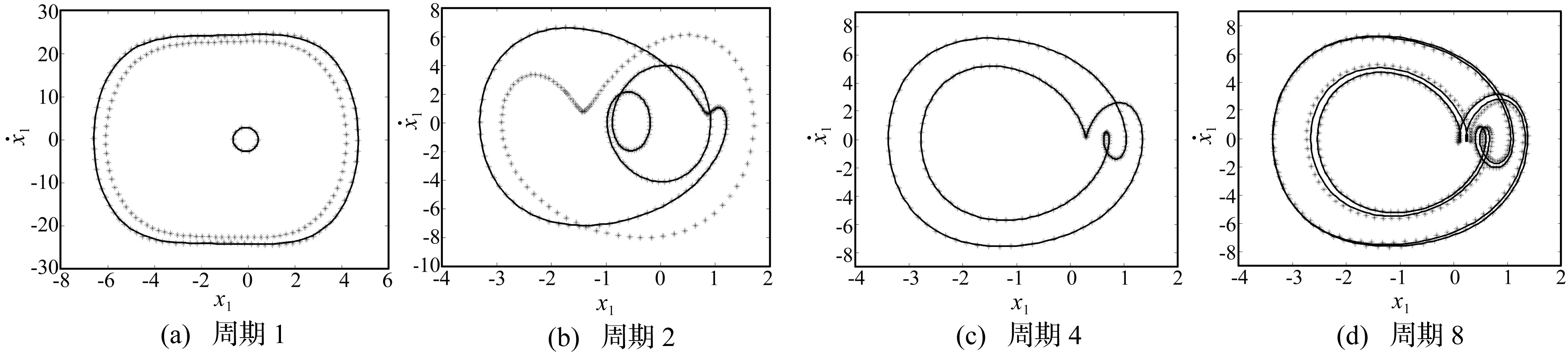
圖2　諧波平衡法與數值計算得到的系統相圖Fig.2 Phase diagrams obtained by using harmonic balance method and numerical simulations

2.3穩定性分析

次諧波失穩將會產生下一級的次諧波，因而通過分析次諧波的穩定性，可以得到下一級次諧波產生的邊界，以及新產生的次諧波形式。通過分析變分方程(Hill方程)的解來可判斷定常解的穩定性以及失穩的方式，該方法是基于Floquet理論進行的，對于弱非線性系統可以轉化為求解Mathieu方程的穩定邊界問題，但是對于強非線性系統，該方法失效，只有直接對Hill方程解的形式及穩定邊界進行分析。

通過上述方法得到式(3)中各傅里葉系數后，便求得定常解xi0。要分析定常解穩定性，需要對其進行擾動，即在式(3)上疊加一個小的擾動量：

xi=xi0+ui,(i=1,2)

(9)

將式(9)代入式(2)，并考慮xi0滿足方程(2)這一事實，將得到的關于ui的方程線性化，可以得到：

(10)

式(10)第二式為線性微分方程，確定的是u2與u1幅值與相位之間的比例關系，而決定系統穩定性的為第一式。將式(3)代入(10)，這樣便得到了Hill方程：

(11)

ρ=-arctan(b1,1/a1,1)

這樣對周期解(3)的穩定性分析轉化為了Hill方程解的穩定性分析。Hill方程屬于周期系數的參數激勵系統，對于該系統的分析可知，系統不穩定區域邊界與η0有關，根據不同的η0值，在不穩定區域可能存在兩種不同形式的解。

(12)

(13)

式(12)、(13)中i=1,2。在邊界上有ζ=0。式(12)的周期為2T，其中T為式(2)激勵力周期，因此可以認為當系統以式(12)方式失穩時，系統將發生倍周期分岔，通過求解系統以式(12)方式失穩的邊界就可以得到倍周期分岔的分岔值。以(13)方式失穩時，系統將發生鞍結分岔，通常這種情況與折疊點的存在相伴。對于更高層級次諧波和更高截斷階數，可以利用maple等符號計算軟件進行計算。

3分岔分析

前面的分析可以得到，按照式(13)方式失穩時，發生鞍結分岔，而以(12)方式失穩時，系統在ω/2次諧共振區域會進一步發生倍周期分岔，從而產生2T、4T、8T…，直至最后產生混沌運動。

3.1B1分岔過程

圖3　倍周期分岔序列中各級次諧波的幅頻特性曲線Fig.3 Amplitude-frequency curves of the subharmonics in the cascades of period-doubling bifurcations

3.2B2分岔過程

數值計算得到系統分岔圖如圖4所示。對比圖3可以看出，由諧波平衡法得到的各分岔值與數值計算吻合得很好，混沌區域右邊界值也與數值計算得到的混沌區域右邊界值4.467吻合較好，但是左邊界值卻與數值計算相差較大，其原因有可能是由于混沌吸引子的邊界激變(chaotic boundary crisis)[14]引起的。隨著ω的減小，混沌吸引子在相空間中不斷膨脹，最終與穩定的周期1吸引子的吸引域邊界碰撞，因而混沌吸引子連同其吸引域突然消失，這樣使得混沌運動的左邊界提前出現，混沌參數區域減小。

圖4　分岔圖Fig.4 Bifurcation diagram

4結論

本文將諧波平衡法與跟蹤延拓算法相結合，深入研究了強非線性隔振系統的諧波響應及其穩定性，并對典型的倍周期分岔道路進行了細致分析，得到了如下結論：

(1) 強非線性隔振系統中存在著多級次諧波，上一級次諧波失穩將導致下級次諧波的產生。諧波失穩方式有兩種，分別對應著倍周期分岔與鞍結分岔；

(2) 可以通過分析系統變分方程的穩定性，從而得到倍周期分岔點與鞍結分岔點，并且可以將穩定倍周期分岔點的聚點作為混沌區域的邊界，諧波平衡法得到的結果與數值計算結果吻合較好；而非穩定倍周期分岔點的聚點并不能作為混沌區域的另一個邊界，這與Kapitaniak的結論并不完全一致。

上述分析對于理解非線性隔振系統周期運動狀態的各種特性以及經過倍周期分岔進入混沌的過程有重要意義。

[ 1 ] Yoon J, Singh R. Examination of super-harmonics in a multi-degree of freedom nonlinear vibration isolation system: Refined models and comparison with measurements [J]. Mechanical Systems and Signal Processing, 2014, 48(1/2): 368-387.

[ 2 ] Peng Z K, Meng G, Lang Z Q, et al. Study of the effects of cubic nonlinear damping on vibration isolations using Harmonic Balance Method [J]. International Journal of Non-Linear Mechanics, 2012, 47(10): 1073-1080.

[ 3 ] 黃志偉，何雪松，陳志剛，等. 非線性隔振系統振動特性分析[J]. 動力學與控制學報, 2013, 11(3): 252-257.

HUANG Zhi-wei, HE Xue-song CHEN Zhi-gang, et al. Research on the vibration characteristics of nonlinear isolation system[J]. Journal of Dynamics and Control, 2013, 11(3):252-256.

[ 4 ] 孟宗，付立元，宋明厚. 一類非線性相對轉動系統的組合諧波分岔行為研究[J].物理學報， 2013,62(5)：054501(1-10).

MENG Zong, FU Li-yuan, SONG Ming-hou. Bifurcation of a kind of nonlinear-relative rotational system with combined harmonic excitation[J]. Acta Phys. Sin., 2013, 62(5)：054501(1-10).

[ 5 ] 魏靜，孫偉，褚衍順，等. 斜齒輪系統分岔與混沌特性及其參數影響研究[J]. 哈爾濱工程大學學報, 2013, 34(10):1301-1309.

WEI Jing，SUN Wei，CHU Yan-shun, et al. Bifurcation and chaotic characteristics of helical gear system and parameter influences[J]. Journal of Harbin Engineering University, 2013, 34(10):1301-1309.

[ 6 ] Li T Y，Yorke J A．Period three implies chaos [J]．Amer．Math．Monthly，1975，82：985-992．

[ 7 ] 閆振華，王國強，蘇麗達，等.非線性被動隔振器剛度特性研究[J].振動與沖擊,2013,32(19):139-143.

YAN Zhen-hua, WANG Guo-qiang, SU Li-da, et al. Stiffness characteristics of a non-linear passive vibration isolator[J].Journal of Vibration and Shock, 2013, 32(19): 139-143.

[ 8 ] 張敬,徐道臨,李盈利,等. 多源激勵下雙層隔振浮筏系統的線譜混沌化[J]. 物理學報，2014,63(18)：18050501-18050511.

ZHANG Jing, XU Dao-lin, LI Ying-li, et al. Line spectrum chaotification of a double-layer vibration isolation floating raft system under multi-source excitation[J]. Acta Phys. Sin., 2014,63(18): 18050501-18050511.

[ 9 ] Lukomsky V P，Gandzha I S．Cascades of subharmonic stationary states in strongly non-linear driven planar systems [J]．Journal of Sound and Vibration，2004，275：351-373．

[10] Yu X，Zhu S J，Liu S Y，Bifurcation and chaos in multi-degree-of-freedom nonlinear vibration isolation system[J]．Chaos，Solitons and Fractals，2008，38：1498-1504．

[11] Blair K B，Krousgrill C M，Farris T N．Harmonic balance and continuation techniques in the dynamic analysis of Duffing’s equation [J]．Journal of Sound and Vibration，1997，202：717-731．

[12] 楊忠華．非線性分歧：理論和計算[M]．北京：科學出版社，2007．

[13] Kapitaniak T．Chaos for engineers-theory，applications，and control [J]．Berlin：Springer-Verlag，2000．

[14] Grebogi C，Ott E，Yorke J A．Chaotic attractors in crisis [J]．Phys．Rev．Lett．，1982，48：507-1510．

Subharmonic and bifurcation analysis for a high-dimensional strongly nonlinear vibration isolation system

HE Qi-wei1, YU Xiang1, MAO Wei-min2

(1. Office of Research and Development, Naval University of Engineering, Wuhan 430033, China;2. Zhejiang Kailin Ship Factory, Zhoushan 316000, China)

Cascades of subharmonic waves and their stability for a high-dimensional strongly nonlinear vibration isolation system were studied by combining the harmonic balance method and the predictor-corrector method. The amplitude-frequency curve of every subharmonic wave was plotted. Two routes of bifurcation were analyzed and the boundaries of the period-doubling bifurcations were obtained through the stability analysis, and then the parametric regions of chaos were estimated. The results agreed well with those obtained with numerical simulations.

nonlinear; subharmonic; bifurcation; chaos

10.13465/j.cnki.jvs.2016.11.010

國家自然科學基金(51009143)

2014-11-27修改稿收到日期：2015-04-30

何其偉 男，博士, 副教授，1972年生

俞翔 男，博士，高工, 1978年生

E-mail：yuxiang898@sina.com

O322；O328；U664

A