高中數學的K—W—L教學策略

趙靜

[摘 要] 針對高中數學的教學而言，有很多值得教師深思的問題，例如怎樣從學生已有的知識和經驗出發，在課堂中進一步幫助學生建構新的知識體系，形成新的學習認知？怎樣在教學過程中激發學生對所學內容的好奇心？怎樣在和諧的問題情境中進一步激發學生的數學思維，促進教學相長？以上問題是值得數學教育者認真思考的問題，就此，美國學者Carr.E.和Ogle.D.等所提出的K-W-L教學策略，對解決以上問題提供了有效的參考.

[關鍵詞] 高中數學；K—W—L教學策略；拋物線的標準方程

以“拋物線的標準方程”為例來探索高中數學的K—W—L教學策略

1. 教學目標

針對“拋物線的標準方程”的教學，教學的重點應該放在拋物線的定義及其標準方程上，在此基礎上，讓學生進一步掌握利用標準方程求取焦點坐標和準線方程的方法. 另外，利用對拋物線標準方程的探索過程，讓學生明確建立適當平面直角坐標系的方法和意義，進一步體會數學思維的力量.

2. 教學設計

在這節課的教學設計中，筆者采用的是雙曲線和橢圓的教學思路，通過深入這種教學思想，使學生在教師的引導下，能夠積極思考相關教學知識，并以自己原有的知識建構為基礎，提出自己對拋物線教學知識的認識和理解. 具體的教學設計內容見表1：

“問題”是數學教學的核心，對此，教師以問題為引領，引導學生步步深入，對學習任務進行探索.針對拋物線內容的教學，本節內容的教學設計主要以K—W—L教學策略為指導，以提出問題、解決問題為主線，將教學過程分為三個學習階段，從而實現本節課的教學目標.

3. 教學過程

（1）what I know

“what I know”是教學過程中的第一個學習階段. 展開教學活動之前，相關的教學目標和教學任務已經確立，因此，教師可以對學生明確課堂的教學主題：拋物線的標準方程. 然后，對學生提出問題：通過以往解析幾何的學習，我們已經掌握了哪些知識內容？

在此，教師對學生提出的是一個具有引領性的問題，目的是啟發學生去思考，去回憶，讓學生對自己已有的知識結構進行了解. 然后以自己的知識經驗為基礎，對自己以往學過的解析幾何知識進行重組，深化認識. 學生在問題的引領下，充分發揮自身學習的主觀能動性，通過思考或者互助學習的方式，認真回憶并回答了以下問題：

問題1：直線、圓、橢圓、雙曲線這些曲線的形狀是怎樣的，它們的方程表達式又是什么？

問題2：拋物線的定義是什么？

問題3：對于曲線方程的建立，一般有哪些步驟？

問題4：在求曲線方程的過程中，有沒有一些簡便的方法和技巧？

在此，教師需要注意，利用問題的方式來對學生進行啟發的過程中，要考慮到一定的邏輯性. 否則，學生會很籠統地對自己已學到的知識進行搜尋. 這樣做可以達到兩個目的：一是幫助學生更加深入地了解本節課的教學；二是與學生一起對之前學過的知識進行回憶和鞏固.

（2）what I want to know

“what I want to know”是教學過程的第二個階段，教師對學生拋出問題：“拋物線的標準方程”是我們今天著力研究的教學問題，你們認為需要研究的內容有哪些？

課堂中，通過教師的引導，學生發揮合作學習的精神，就此問題展開討論.過后，教師檢查學生對問題的思考成果，讓學生將自己認為需要研究的問題寫在黑板上，以此作為本節課教學的任務. 對此，師生合作，解決第一個問題：

問題1：如何建立平面直角坐標系來求拋物線的方程？

對此，教師以學生為對象，在黑板上進行演示：以豎直方向為準，先畫出一條定直線l，再畫出直線l右側的一個點F，然后，利用距離相等的特性畫出一條開口向右的拋物線.

問題（1）：在畫出拋物線的過程中，確定的條件是什么？

學生：點F與直線l之間的距離. 然后，教師對學生的問題進行反饋：我們將這個距離設為P.

問題（2）：拋物線的曲線方程要怎么求呢？

學生：建系—設點—列式—化簡.

問題（3）：建立平面直角坐標系的時候需要注意什么嗎，怎樣建比較好呢？

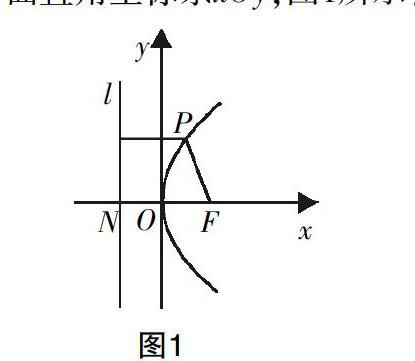
學生經過思考，展開互助學習，積極討論、比較，然后發言. 接著，全班一起比較、說明，最終派一位學生代表進行展示：設定點F，過點作直線FN與直線l垂直，垂足為N. 然后以直線NF為x軸，將線段NF的垂直平分線設為y軸，并以此建立平面直角坐標系xOy，圖1所示：

問題（4）：那么你們有誰可以說出拋物線的標準方程呢？

師生合作，共同探索，學生思考，積極發言，最終形成拋物線的標準方程：y2=2x.

問題2：在拋物線圖象中，如果其焦點變換位置，那么拋物線的方程會發生怎樣的變化呢？

學生經過知識積累和感悟，然后發言：如果焦點是在x軸的負半軸上，那么拋物線的標準方程會變為：y2=-2px，如果焦點是在y軸的負半軸上，那么拋物線的標準方程變為：x2=-2py；如果焦點是在y軸的正半軸上，那么拋物線的標準方程變為：x2=2py；學生在獲得知識的基礎上進行總結，可以拋物線的定義列式為基礎，進一步得出焦點發生變化時的拋物線的方程，最終，在學生的討論下，拋物線的四種表現形式得以體現.

問題3：求取曲線方程的過程是什么？

就此問題而言，教師需要對學生加以引導，引導學生去總結，并進行“統合”.在教師的引導下，以拋物線知識的學習為基礎，學生很容易歸納出求取曲線方程的一般過程：建系—調整—設點—列式—化簡.

學習的最終目的是能夠應用，因此，教師與學生一起探索出拋物線標準方程的四種形式之后，要及時地讓學生對其加以應用. 在此，教師可以為學生設置一些具有代表性的數學題目，例如：“y2=4x，x2=2y，y=-2x2”，讓學生學會求拋物線的焦點坐標和準線方程.

問題4：如何確定拋物線的方程？

在此問題的解決上，教師可以利用設置習題的方式，讓學生自己去總結確定拋物線標準方程的基本條件.在習題的設置上，例如：以下列條件為依據，求出拋物線的標準方程. 條件1：焦點（6，0）；條件2：過點P（-2，-4）；條件3：焦點在直線x+3y=15上. 設置這個教學環節的目的是提高學生解決問題的能力，培養應用知識的能力，讓學生在實踐的基礎上獲得新的知識.

（3）what I learned

“what I learned”是教學過程的第三個階段，即：通過這節課的學習，我們學到了什么？具體讓學生明確下列問題：問題1：本節課中，我們學到的知識有哪些？問題2：在這節課中，我學到了哪些方法？問題3：研究解析幾何的過程中，通常用到的方法是什么？問題4：我可以解決哪些數學問題？最后，教師要為學生布置課后作業，對他們的學習效果做一個檢查，同時利用作業中的問題以及學生的反饋來改進自己的教學.

此階段在K—W—L教學策略中占有相當重要的地位，因為它是對教師教學成果和學生學習效果的一個總結和評價.教師除了領導學生探索課堂問題，還可以利用具有總結性的習題對學生加以考驗.另外，在對學習知識進行總結的過程中，教師可以利用列表的方式，將四種方程的標準公式、焦點以及標準方程的坐標給羅列出來，讓學生明確本節課教學中需要掌握的主要知識點.

結語

總的來說，在高中數學教學過程中引入K—W—L教學策略，有利于實現高中課堂教學的改革，進一步提高高中數學教學的效率. K—W—L教學策略，即將教師的教學過程分為三個階段：what I know（已經知道的知識）、what I want to know（通過學習想要知道什么）、what I learned（通過學習，真正掌握到了什么），具體的課堂教學中，教師通過實施這三個教學階段來達到自己的教學目的.針對K—W—L教學策略的運用，筆者以拋物線及其標準方程的教學為例，對相關的教學目標和教學過程進行了設計，有效地激發了學生的學習興趣，增強了學生對新知識的接受能力.