用祖暅原理求平面圖形面積

胡娟娟

[摘 要] 為了求“非標準”的平面圖形面積，本文借助原理，把“非標準”的平面圖形進行空間平移轉化為“非標準”的幾何體，然后求出該幾何體體積，再由體積公式求出該平面圖形面積. 通過推廣該方法可以用于求由一次函數或二次函數所圍成的幾何圖形的面積.

[關鍵詞] 祖暅原理；非標準幾何體；非標準平面圖形；面積

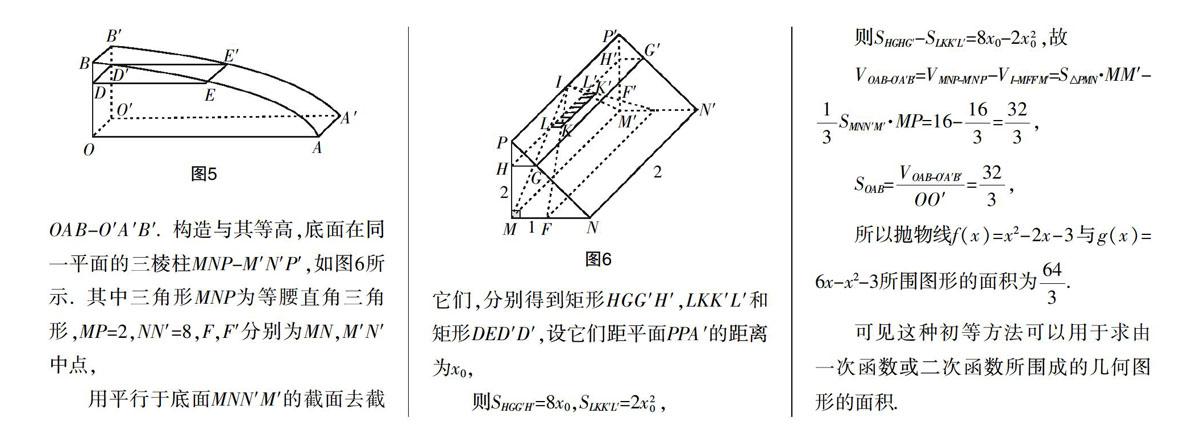
用初等方法求幾何體體積時，常常借助于祖暅原理，事實上，祖暅原理除了運用于解決不規則幾何體的體積，還可以求解平面圖形的面積. 《由祖暅原理想到的——求曲邊三角形面積的初等方法》一文（裴光亞）利用祖暅原理給出了求曲邊三角形面積的初等方法，筆者嘗試對曲邊三角形進行推廣.

祖暅原理：夾在兩個平行平面間的兩個幾何體，被平行于這兩個平面的任意平面所截， 如果截得的兩個截面的面積都相等， 那么這兩個幾何體的體積相等.

由于祖暅原理易求“非標準”幾何體體積，筆者聯想到把“非標準”平面圖形通過空間平移轉化為“非標準”幾何體，通過祖暅定理求出該幾何體體積，然后再由體積公式求出該平面圖形面積.下面我們看一些具體應用.

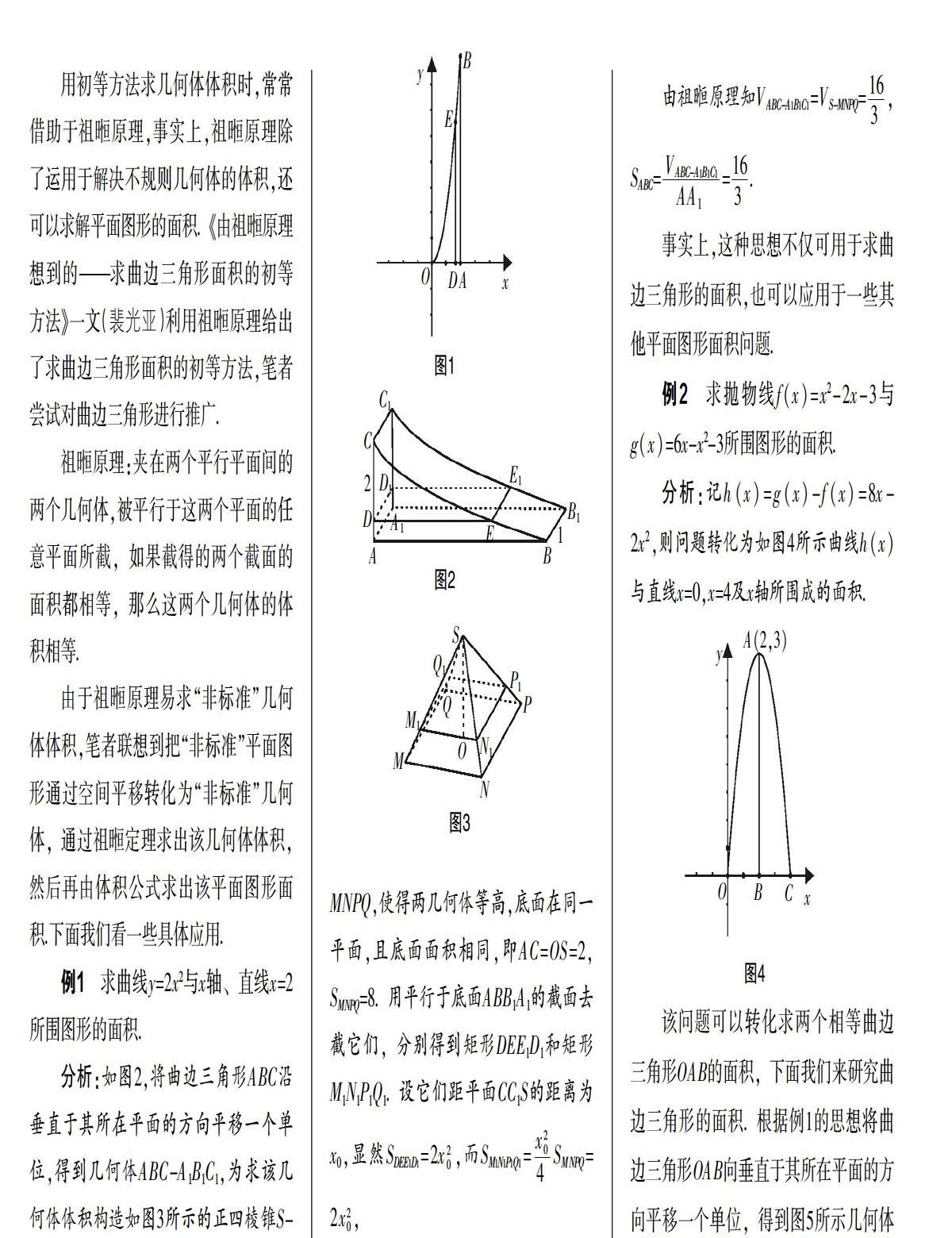
例1 求曲線y=2x2與x軸、直線x=2所圍圖形的面積分析：如圖2，將曲邊三角形ABC沿垂直于其所在平面的方向平移一個單位，得到幾何體ABC-A1B1C1，為求該幾何體體積構造如圖3所示的正四棱錐S-MNPQ，使得兩幾何體等高，底可見這種初等方法可以用于求由一次函數或二次函數所圍成的幾何圖形的面積.