經歷形成過程 促進理解建構

【關鍵詞】函數；教學設計；初中數學

【中圖分類號】G633.6 【文獻標志碼】A 【文章編號】1005-6009（2016）33-0068-03

【作者簡介】王新奇，江蘇省蘇州工業園區星灣學校（江蘇蘇州，215021）教科室主任，一級教師。

一、設計理念

1.概念形成要讓知識邏輯與心理邏輯自然融合。

概念的形成過程應是學生知識邏輯與心理邏輯的自然融合。在教學“函數”這一概念時，應始終抓住一個變化過程、兩個變量、一種對應關系進行探究，讓學生知道往哪里走。在探究兩個變量之間的關系時，應始終將“一個量變化時，另一個量如何變化；一個量確定時，另一個量是否確定”作為思考的切入點，讓學生知道觀察的點在哪里。在提煉概括函數定義時，應圍繞一個變化過程、兩個變量、一種對應關系進行表述，以期達到水到渠成的效果，促進學習的真正發生。

2.概念理解要抓住關鍵字詞。

函數的定義表述是初中數學學習中文字最長的，學生要做到準確理解有一定的困難。教學中，從細節上找到“每一個值”“唯一值”，按層次將關鍵字詞標出，會對理解定義起到化難為易的效果。

3.概念應用要回歸定義本質。

學習函數概念，其根本目的在于讓學生用函數的觀點認識生活中變化的事物，只有把握了變化事物中兩變量之間的對應關系才算是掌握了函數的本質。圍繞函數定義的本質，設計不同層次的問題進行訓練，以提高課堂訓練的針對性與有效性。其中，我所設計的第3道練習題是一道開放性的問題，引導學生嘗試提出問題、解決問題，目的是給學生獨立思考、合作交流的機會，也是在檢驗學習是否真的發生。

二、學情分析

1.學生原有知識的分析。初中生在函數概念形成之前，研究的是常量數學——數、式的運算和方程。函數概念是從常量數學到變量數學的轉折點，學生缺乏對變量數學的了解，因而也缺乏同化函數概念的固著點，給學生學習帶來一定的困難。函數概念的形成過程，其本質是學生建構數學認知結構的過程。函數概念和學生原有的認知結構無直接聯系，因此，通過4個生活情境，建構這類問題的問題系，從而使學生建構良好的認知結構，為同化函數概念做好準備。

2.學生原有生活經驗的分析。4個情境的選擇均源于學生的生活，充分利用學生原有生活經驗，引領學生經歷函數概念的形成過程，能有效促進學生理解函數概念本質，促進學習的真正發生。

3.學生的情感分析。函數概念由模糊到清晰經歷了近300年，足以說明其困難程度。在本節課的教學中，筆者多次采取小組合作交流學習的方式，消除學生情感上的畏懼，同時選擇貼近學生生活實際的情境進行研究，促進學生積極、有效地學習。

三、教材分析

本節課所用教材為（蘇科版）《義務教育教科書·數學八（上）》，所教內容為第6章第1節“函數”的第1課時。函數概念的建立，標志著學生對數學的學習已從常量數學邁向變量數學。函數是“數與代數”中的重要內容，是學生難以建立的一個抽象數學概念。讓學生準確而深刻地理解函數概念是學好與函數相關內容的關鍵所在，是后續學習一次函數、反比例函數、二次函數的奠基工程，是高中階段學習其他函數的必要準備，同時也是培養學生用運動變化的觀點分析問題和解決問題的有效載體。通過對變量之間對應關系的研究有利于增強學生綜合運用數學知識的意識，有利于提高學生的數學素養和綜合能力。教材從學生似曾相識的實例中引出對變量的認識，讓學生在發現問題的共同點中形成函數概念，這種處理問題的方式遵循了學生的認知水平，關注了學生的親身體驗，體現了循序漸進、由具體到抽象的原則。

四、教學目標及重點、難點

1.教學目標。

（1）通過簡單實例，了解常量與變量的意義。

（2）讓學生經歷分析具體問題中變量之間對應關系的過程，感知函數是描述變化過程的一個數學概念；讓學生經歷從幾個簡單的具體問題中找出共同點，逐步過渡到抽象定義的過程，從一個變化過程、兩個變量、一種對應關系中領悟和理解函數概念。

（3）讓學生學會用函數的觀點觀察、分析現實生活中的簡單問題，初步學會建立簡單的函數模型，不斷培養學生學習和運用數學的能力。

2.教學重點、難點。

教學重點：函數概念的形成過程。

教學難點：理解函數概念中的對應關系，深刻理解和靈活應用函數概念。

五、教學過程

（一）問題情境

問題1：同學們知道給汽車加油嗎？在給汽車加油的過程中，一般關注哪幾個量？

問題2：在給汽車加油的過程中，這幾個量有變化嗎？

（設計意圖：從學生身邊的生活實例出發，引發學生的思考。播放給汽車加油的視頻，生動展現幾個量的變化情況，加深學生對這幾個量的認識，既貼合課題，又易于撥動學生的思維之弦。通過這個問題情境，一方面引出常量與變量概念，另一方面有意識滲透“在某一變化過程中”這個建立函數概念的前提條件，為分析變量之間的一種對應關系做準備。）

（二）建構活動

情境1：讓學生觀看給汽車加油的視頻（如圖1所示）。

（師生互動：同學們喊“開始”，老師就點擊開始，同學們喊“停”，老師就點擊暫停。）

提出問題：這兩個變量是如何變化的？你能用一段話來描述這兩個變量之間的關系嗎？

情境2：南京某日氣溫變化圖（如圖2所示）。

2013年10月1日南京市整點氣溫曲線圖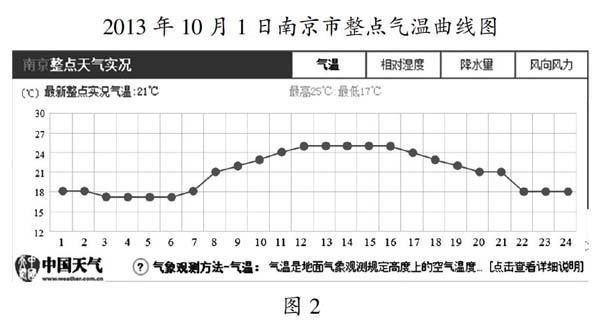

提出問題：在南京某日氣溫變化圖中，有哪兩個變量？請描述在氣溫變化過程中，時間和氣溫這兩個變量之間的關系。

情境3：觀察水庫的水位變化與水庫蓄水量變化表（如表1所示）。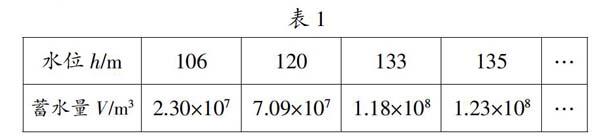

提出問題：在水庫蓄水量變化過程中，有哪兩個變量？請描述在水庫蓄水量變化過程中，水位和蓄水量這兩個變量之間的關系。

情境4：“搭小魚”火柴游戲（如圖3所示）。

提出問題：在“搭小魚”游戲的過程中，有哪兩個變量？請描述小魚的條數和火柴根數這兩個變量之間的關系。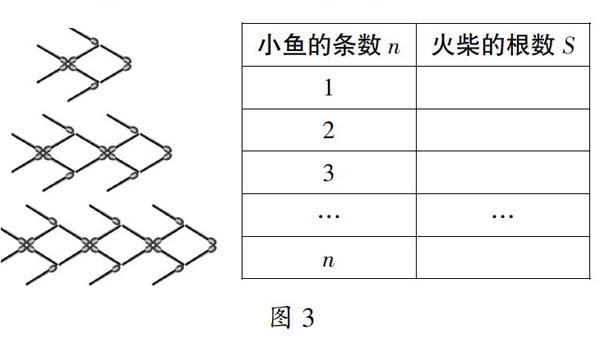

（設計意圖：通過觀察這4種情境，引導學生認識情境中的變量，并描述變化過程中變量之間的關系。這樣設計，一方面能讓學生清晰地體會到觀察點在哪里，發展學生的認知邏輯；另一方面學生通過圖表、圖象和表達式能夠清晰地揭示兩個變量之間的關系。）

（三）數學化認識

問題1：剛才研究了4個生活情境，你發現有哪些共同點？

問題2：誰能嘗試著給函數下一個定義？

函數定義：如果在一個變化過程中有兩個變量x和y，并且對于變量x的每一個值，y都有唯一的值與它對應，那么我們稱y是x的函數，其中x是自變量，y是因變量。

問題3：誰能說一說定義中的關鍵字詞？

問題4：誰能說一說在我們的生活中有關函數的例子？

（設計意圖：通過深入研究4個生活情境，充分感受和理解一個變化過程中兩個變量之間的關系，并引導學生圍繞“一個變化過程、兩個變量、一種對應關系”歸納出函數的定義。在實際教學中，學生的回答不一定很到位，幾經磨礪再形成定義才是真實的。學生對函數的表述一定是自己容易理解的，一定是理解很深刻的，這樣的學習才會真正發生。作為教師應有不迷信教材而賞識學生的胸懷和膽識，把學術的知識形態轉化為真實的教育形態才是教師所必須努力的。讓學生從熟知的實例到函數概念形成，會覺得函數好學。問題3的設計讓學生從細節上找到“每一個值”“唯一值”，按層次將關鍵字詞標出，對理解定義起到了化難為易的效果。舉例的目的是讓學生逐步領會函數的定義，逐步學會從函數的視角觀察分析實際問題，形成實實在在的能力，有助于學生對函數的認識，有助于學習的真正發生。）

（四）嘗試運用

1.用一根40cm的繩子圍成一個長方形，

（1）當長方形的寬為5cm時，長為 cm；

（2）當長方形的寬為8cm時，長為 cm；

（3）當長方形的寬為acm時，長為 cm；

（4）長方形的長是寬的函數嗎？為什么？

2.下表中的y是x的函數嗎？為什么？

3.如圖4，線段AB=6cm，D是線段AB上的一個定點，在垂直于AB的線段DE上有一個動點C（點C與點D不重合），分別連接CA、CB。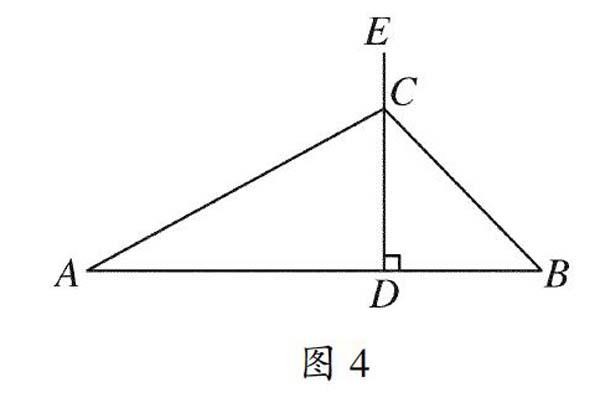

（1）請說出圖形變化過程中的常量與變量。

（2）結合今天所學的函數知識，你還能提出什么問題？

（設計意圖：第1題和第2題是進一步加強學生對函數概念的認識。對剛剛接觸函數概念的學生來說，判斷兩個量之間是否具有函數關系需要把握三點——一個變化過程、兩個變量、一種對應關系。第3道練習，設計了一道開放性的問題，引導學生結合所學習的知識嘗試提出問題、分析問題、解決問題，目的是給學生獨立思考、合作交流的機會，幫助學生理解，也是在檢驗學習是否真的發生。）

（五）分享與作業

觀察生活與社會，你能發現哪些實際問題與函數密切相關，并能用函數思想予以解決，把你的想法告訴你的同伴與家人。

結語：函數是我們在學習方程、不等式、概率之后的又一個數學模型。世界是變化的，生活中的變化無處不在，函數正是研究運動變化的重要模型，函數就在我們身邊，希望同學們認真學習函數。學習的效果與我們的勤奮程度也成函數關系，希望大家通過自己的勤奮獲取學習效果的最大值。

（設計意圖：通過結語，把函數納入學生的知識結構，對學生的后續學習產生激勵作用，通過開放性作業，讓學生在成功中獲得最大的心理滿足感。）