順應內在需求 豐盈數學經驗

崔海華

[摘 要]課堂教學中，教師應當尊重學生已有的數學認知和經驗，順應學生的內在需求，挖掘課堂生成背后的深層次原因，讓“教”契合學生的“學”。這樣既使數學課堂走向自然、深刻，又使學生獲得應有的數學成長，凸顯數學教學的價值。

[關鍵詞]內在需求 數學經驗 順應 重構 數學教學

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）29-021

課前我預測，第二種思路無論是書寫過程，還是思考過程，比另外兩種思路都要簡潔、有效，且基于學生課前先學的基礎之上，顯然應該作為學生首選的解決方法。但在教學中，學生首先想到的并不是這三種解決問題的思路，而是根據“圖上距離∶實際距離=比例尺”轉化得到的關系式“圖上距離÷比例尺=實際距離”，列除法算式求解。

思考：

教材上提供的簡潔有效的思路卻不受學生青睞，教材上沒有的思路學生反而容易接受，讓人不禁思考以下問題：教材的編排與學生思考原點間究竟有哪些不可逾越的鴻溝？究竟如何正確定位教材提供的方法在學生學習中的作用和地位？怎樣才能從更加寬廣的數學發展的角度，從有利于學生成長的視角，引導學生在方法的多樣化和優化之間找到適切的平衡點呢？

基于以上問題，在認真學習蘇教版《義務教育課標實驗教科書數學教師用書》中的教學建議，及與六年級學生進行了較為深入的交流后，我進行了深入的思考。我覺得，教學中只有充分尊重學生已有的數學認知和經驗，順應學生的內在需求，才能真正突顯數學教學的價值，讓“教”契合學生的“學”，使學生獲得應有的數學成長。

第一，契合學生的思維特點。

關系式“圖上距離÷比例尺=實際距離”的求解方法是學生在理解比例尺意義的基礎上得到的，因此為順應學生的學習需要，教學中應將此關系式與書本提供的方法一起出示，讓學生感受到解決問題的策略是多樣化的。

第二，基于學生的學習現實。

從教師的角度看，書上的第二種思路是最簡潔的，但從學生的角度看，第二種思路雖然列式簡單，可列式之前必須要經歷8000厘米=80米改寫的過程，思維難度的增加意味著解決問題的難度同時增加，這大約是學生不能普遍接受第二種思路的原因吧！

第三，恰當定位方法的多樣化與優化。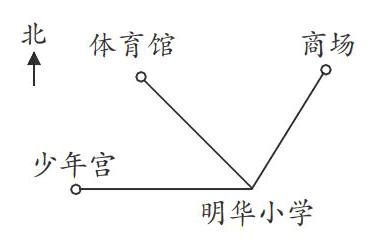

課堂上，當把學習的主動權交給學生時，所有的解題思路學生都有可能會出現。所以，教師在教學中既要放手讓學生充分展示思考過程，又要注意引導學生在多種解決問題方法的比較與反思中，實現方法的優化，使每位學生都能得到符合自身思維發展水平的解決方法。

重構：

一、合作探究，形成解決問題的思路

1.舊知導入

（1）關于比例尺，同學們有什么可以跟大家分享的嗎？比例尺1∶500表示什么意思？

（板書：圖上距離∶實際距離=比例尺）

（2）今天，我們在此基礎上學習比例尺的應用。

2.探究方法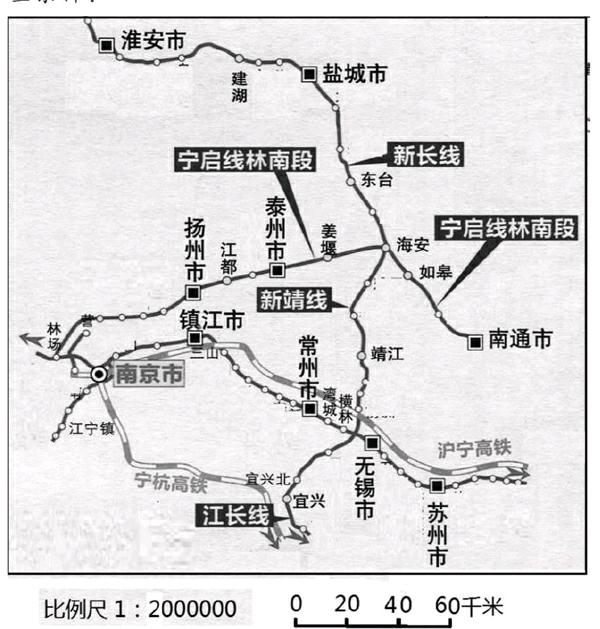

（1）根據明華小學附近的平面圖（如下），能求出明華小學到少年宮的實際距離嗎？應該怎么辦？

①添上條件“比例尺1∶8000”后，學生動手測量，得出圖上距離是5厘米。

②根據條件獨立解決問題并交流。

方法A：由“圖上距離∶實際距離=比例尺”得出“圖上距離÷比例尺=實際距離”，列式為5÷■=40000（厘米）=400（米）。

方法B：根據實際距離是圖上距離的8000倍，列式為5×8000=40000（厘米）=400（米）。

方法C：根據比例尺1∶8000，可知圖上1厘米表示實際距離80米，用乘法算式5×80=400（米）來解決。

方法D：根據比例相同，用解比例的方法來求解。解：設明華小學到少年宮的實際距離是x厘米。列式為5∶x=1∶8000，求得x=40000，40000厘米=400米。

（2）你能比較一下這幾種方法的異同嗎？你最喜歡哪一種方法，能說說理由嗎？

【設計意圖：在缺少條件的基礎上，有效調動學生已有的對比例尺的數學經驗，使他們主動尋找有用信息解決問題。多種解決方法的呈現與優化，既是引導學生從不同角度理解比例尺的意義，又是對解決方法的再審視、再提高。同時，方法沒有優劣，學生可以在比較的過程中找到最適合自己的那種方法。】

（3）試一試：明華小學正北方240米是醫院，你能在圖中表示出醫院的位置嗎？用自己喜歡的方法完成。

（4）引導反思：剛才我們解決了哪兩個問題？都是根據什么來解決的及是怎么解決的？

【設計意圖：通過反思引導學生梳理解決問題的過程，這對于幫助學生積累解決問題的基本經驗、構建比例尺問題的解題模型和提升數學思維水平，具有重要意義。】

二、比較優化，感悟比例尺的價值

1.線段比例尺的數學價值

（1）出示江蘇省部分鐵路交通圖（如下圖），問：如果要求出南京到南通的直線距離是多少千米，需要知道哪些條件？

生：需要知道圖上距離和比例尺是多少。

（指名學生測量出圖上南京到南通的距離約為10厘米，并計算出兩地的直線距離）

（2）你最喜歡哪一種方法？為什么？

生：最喜歡用線段比例尺求解，這樣比較簡便。

（3）前面兩道題為什么沒想到用這種方法去求解？什么情況下使用這種方法比較簡便？

2.比例尺的靈活轉化

（1）公開出版發行地圖的比例尺是有規定的，這個規定的比例是怎樣的呢？（引導學生閱讀書本上“國家基本比例尺地圖”的知識）

（3）列式計算。

②在比例尺1∶500000的地圖上，南京到南通的直線距離是多少厘米？

（4）為什么在不同地圖上的直線距離，長度不一樣呢？你發現其中什么是相同的？這說明什么？

（5）出示：南京站到南通站長途汽車的里程約是253公里，乘坐火車全長約284公里。你們從中發現了什么？這到底是怎么回事呢？

【設計意圖：直接把線段比例尺的數據納入計算，既使學生完整地感受比例尺的價值，又為學生所喜聞樂見。在線段比例尺與數值比例尺的比較、不同地圖比例尺上同一實際距離的比較、直線距離與實際行程的比較中，各種比例尺的適用范圍更加突顯，且比例尺的數學價值和學習經驗也在設問思考、動手測量、自主解決問題的過程中進一步得到彰顯與積累。】

三、實踐操作，體驗學以致用的愉悅

（1）課前，我們一起測量出學校籃球場的長是28米，寬是15米。如果讓你在自己的紙上繪制出它的平面圖，需要考慮哪些因素？

（2）考慮作業紙的大小，選用下面哪個比例尺畫圖比較合適？（ ）

A.200∶1 B.1∶200

（3）根據所選的比例尺，計算相關數據，并繪制平面圖。

【設計意圖：課前實地測量并記錄學校籃球場形狀的素材，既讓學生深刻體會到了數學在現實生活中的應用價值，又讓學生在主動學的過程中，積累了應用數學知識解決問題的實踐經驗及形成學以致用的成就感。】

（責編 杜 華）