運用遷移規律，提高課堂效率

劉小玲

摘 ? ?要： 在學習過程中，先前內容的學習對以后內容的學習所產生的影響即是遷移，這些影響有著互相矛盾的兩方面，數學部分知識之間有著內在的聯系和發展規律，教師應依據這一點，使學生已經獲得的有關知識、技能、方法對學習新知識產生積極影響，促使學生的學習由已知向未知轉化。這樣不僅培養了學生的學習能力，而且提高了數學教學質量。

關鍵詞： 正遷移 ? ?負遷移 ? ?數學教學

遷移分為正遷移和負遷移。正遷移能夠對新知識的學習、新技能的掌握產生積極影響。在三年多的教學實踐中，我認為，應該充分利用正遷移，努力排除負遷移。遷移所依賴的主要條件是不同知識存在著共同的因素。在教學新課時，通過發掘新舊知識的共同因素，充分利用這些共同的因素，創設遷移情境，就可以溝通新舊知識間的內在聯系，逐步提高學生學習和探索新知識的能力。例如，教學“三角形的面積公式”時，讓學生把一個平行四邊形剪成兩個完全一樣的三角形，學生很快發現所形成的三角形的面積是原來的平行四邊形面積的一半，從而由平行四邊形的面積公式推導出三角形面積公式。再如此題是九年義務教育六年制小學教科書數學第二冊，第11頁中的一道思考題。書中除圖1-1的圖形外沒有文字說明。這道題旨在引導兒童觀察、思考，初步培養他們的觀察能力。這時兒童已經學過20以內的加減法，基于他們已有的知識，能夠判斷本題的意思是：在右邊大正方形內的小方格中填入數字后，使大正方形中的每一橫行，每一豎列，以及兩條對角線上三個數字的和，都等于左邊小正方形中的數字18。實質上，這是一種幻方，或者說是一種方陣。

圖1-1

現在通過觀察、思考，看小方格中應填入什么數字。從橫中行10+6+□=18會想到，18-10-6=2，在橫中行右面的小方格中應填入2（圖1-2）。從豎右列7+2+□=18（圖1-2）會想到，18-7-2=9，在豎右列下面的小方格中應填入9（圖1-3）。

圖1-2 ? ? ? ? ? ? ? ? ? ? ? ? ? 圖1-3

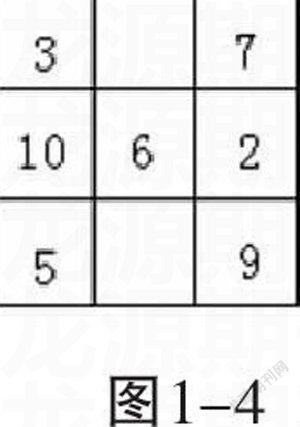
從正方形對角線上的9+6+□=18（圖1-3）會想到，18-9-6=3，在大正方形左上角的小方格中應填入3（圖1-4）。從正方形對角線上的7+6+□=18（圖1-3）會想到，18-7-6=5，在大正方形左下角的小方格中應填入5（圖1-4）。

從橫上行3+□+7=18（圖1-4）會想到，18-3-7=8，在橫上行中間的小方格中應填入8（圖1-5）。又從橫下行5+□+9=18（圖1-4）會想到，18-5-9=4，在橫下行中間的小方格中應填入4（圖1-5）。圖1-5是填完數字后的幻方。對于新舊知識的共同因素比較隱蔽的，則可通過鋪路搭橋，顯示共同因素，促使知識逐步遷移。如，教學兩位數乘多位數的乘法，通過四道準備題，揭示乘法計算的共同點：分別是先乘被乘數的個位數，再乘被乘數的十位數，并以此作過渡，突破積的對位這個難點，實現從一位數乘兩位數向兩位數乘兩位數遷移，使學生掌握計算法則，提高已有知識的概括水平，是促進學習遷移的重要因素。概括水平是有層次的，概括水平高，就能從更高的層次揭示新舊知識共同的本質屬性，促進學習的遷移。例如，看每一行的前三個數，想一想接下去應該填什么數。6、16、26、觀察6、16、26這三個數可發現，6、16、26的排列規律是：16比6大10，26比16大10，即后面的每一個數都比它前面的那個數大10。觀察9、18、27這三個數可發現，9、18、27的排列規律是：18比9大9，27比18大9，即后面的每一個數都比它前面的那個數大9。觀察80、73、66這三個數可發現，80、73、66的排列規律是：73比80小7，66比73小7，即后面的每一個數都比它前面的那個數小7。這樣可得到本題的答案是：6、16、26、36、46、56、66; 9、18、27、36、45、54、63; 80、73、66、59、52、45、38。再如在教學長方形和正方形周長時，書上周長的概念是四條邊長度的和，這個概念只適用于四邊形，對于以后還會學的圓形及多邊形的周長就不適用，而可以把周長的概念提高到“四周圍長度的和”。這樣不管以后學什么形狀的圖形，學生很容易就理解了“周長”這個知識點，可以有力促進正遷移的實現。至于干擾產生的主要原因，是新舊知識存在著易于混淆的因素。

在教學過程中，應通過對比區別出它們的不同點，排除混淆因素，防止原有知識對新知識學習的干擾口。把這種已經獲得的知識對新知識學習的促進作用發揮到最大限度，從而最有利于新知識的掌握。我認為，只要注意引導學生把學到的知識、技能進行整理，弄清彼此聯系、區別，通過數學課堂教學的具體運用把學過的知識加以改造和充實，實現由知識到能力的轉化，充分發揮遷移的有利作用。