滲透數學對應思想 夯實數學思維基礎

呂健威

[摘 要]小學數學的不少內容都有知識上的對應關系存在，因此，教師可以利用對應思想來指導學與教。認識和利用數學對應思想，要由淺入深、由具體到抽象，逐步形成自己的數學思想方法。課堂教學中，教師要把培養學生的對應思想作為數學教學的基本要求，最終達到發展智力、培養多種思維能力的目標。

[關鍵詞]對應思想 滲透 思維方式 夯實

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）14-042

數學中的對應是指人的思維對兩個集合間聯系的把握，“一一對應”的意思就是在這兩個集合中存在一個對一個形成一種相呼應的狀態。教學實踐證明，要找到解決問題的切入點，關鍵要找到誰對應誰，即對應的聯系點，問題將迎刃而解。數學對應思想是一種重要的數學思維方式，在數學中處處存在并被運用。培養學生的數學對應思想是基本的教學要求，對提高學生的計算、分析、解題、作圖等能力有重要作用，為學生數學思維的形成奠定基礎。

一、數形對應思想的滲透

在小學數學教學中重視數形對應思想的滲透，不僅能化難為易，幫助學生理解數學概念和掌握數學技能，而且能潛移默化地使學生養成數形對應的習慣，為進一步理解和發展數學對應思想打下基礎。

1.在用圖解法解應用題中滲透對應思想

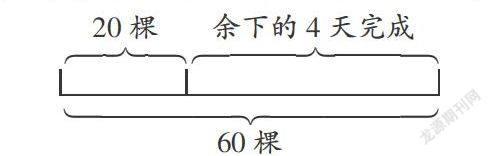
線段圖能準確、明了地展示題中的數量關系，因此，用對應思想分析線段圖中的信息，能正確、快速地解決問題。如：“學校計劃植樹60棵，今天已植樹20棵，余下的在4天完成，余下的平均每天植樹多少棵？”

“60棵”“20棵”和問題都不對應，而“余下的棵數”與問題對應。在找到已知與問題的基礎上，首先要找對應，讓學生根據問題找到與問題相對應的條件，這樣就能把復雜問題簡單化，同時讓學生掌握分析問題、解決問題的方法。

2.在幾何概念中滲透對應思想

在三角形中，有什么樣的底，對應什么樣的高，這就是底與高的“一一對應”。

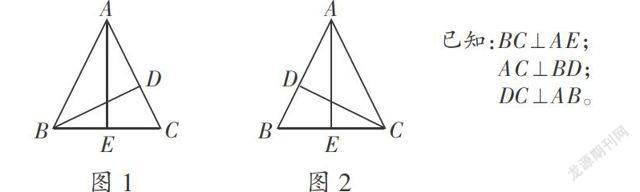
問題：如下圖，求出三角形的面積（單位：厘米）。

用BC×AE÷2或AC×BD÷2求三角形的面積是對的，而BC×BD÷2是錯的，原因是BC底邊與BD不對應，只有找準對應才能列對式子。語文知識上的“底”和“高”的意思跟數學概念上“底”與“高”的含義是有所區別的，運用對應思想會進一步加深對概念的理解。

二、函數對應思想的滲透

如果對于任意的x的值，有完全確定的y的值與之對應，那么稱y為x的函數。這里可以看出，函數思想的本質是對應。因此，教師在指導學生學習數學時，要心中有函數思想，可以利用一些具體的例子，找準哪個量不變，讓某個量“動”起來，或者一個量變化，另一個量也隨之變化，引導學生看出運算結果是隨著哪一個量的變化而變化的，進而從中找出對應關系。

1.在比的知識中滲透對應思想

比的前項和比的后項是兩種相關聯的量，實質上就是函數關系（多元函數情況）。例如，在解決“按比例分配”的問題中，一般來說，已知比的總數量，學生比較容易解決，已知部分數量（或相差量），學生比較難解決，而找準已知數量與比中的哪個項相對應是關鍵。如“男生人數和女生人數的比是5∶6”，即男生人數對應5，女生人數對應6；如果男生有20人，那么比的前項5對應男生20人，女生人數就是20÷5×6=24（人）；如果全班有44人，那么44人對應的是比的前項與比的后項的和，即女生人數是44×6/5+6=24（人）。對應找對了，問題就會輕松解決，也增加了解決問題的樂趣。

2.在四則運算中滲透對應思想

小學數學課本中有填數圖、韋恩圖等內容，并將函數概念滲透在許多例題與練習中。例如，人教版數學五年級上冊第6頁練習（如右圖）：當一個因數固定不變時，積隨著另一個因數的變化而變化。類似的題就計算而言沒什么難度，關鍵是教師在教學這些習題時，要心中有函數思想，可以利用一些能移動的卡片，引導學生從片卡的變化中找出數量對應關系。

3.在幾何公式中滲透對應思想

小學數學中幾何圖形的面積公式和體積公式，以函數的觀點來看，實際上就是用解析法來表示變量之間的函數關系。如長方體的體積V=abh，其體積隨著長、寬、高的變化而變化；圓的面積S=πr2，其面積隨著半徑的變化而變化；一個長方形的面積一定時，一條邊隨著另一條邊的變化而變化……這些公式滲透了冪函數和多元函數的思想。

三、空間對應思想的滲透

1.在“拳頭”與“月份”中滲透對應思想

課堂教學中，教師可引導學生將熟知的事物和某個數學知識產生聯系，實現事物與知識的對應及對新知的認知和理解。如拳頭的凸凹位與月份名稱有著對應的巧合，有的教師沒有強調這個關鍵處，使學生誤以為拳頭含有月份名，造成理解障礙。教師應告訴學生，借助拳頭的凸凹位記大月、小月的知識是一種記憶方法，其中拳頭的凸凹位與大月、小月是一種對應關系。如隨便一只手握緊拳頭且手心向下，數手指與手掌相連的那個關節，從食指起，食指凸出的關節為一月，食指與中指間凹進去的部位為二月，中指凸出的關節為三月，中指與無名指凹進去的部位為四月……重復數這只手從食指起，食指凸出的關節為八月，無名指凸出的關節為12月。凸對應大月，有31天；凹進去的部位對應小月，有30天；2月為特殊月，平年的二月有28天，閏年的二月有29天。

2.在數對知識中滲透對應思想

小學數學空間對應的內容比較欠缺。事實上，教師排座位，在黑板上列一個座位表，下面的學生根據座位表找到自己的座位，這就是空間對應。例如，教學“用數對確定位置”的例1（多媒體出示圖表）時，學生根據小紅在教室的第3列、第1行用數對（3，1）表示，初步建立與座位示意圖的對應關系；在同樣的規則下，再次通過小榮坐在教室的第5列、第2行怎樣用數對表示和給出數對確定位置的活動，加深學生對數對和座位示意圖列與行的一一對應關系。這樣教學既有利于學生直觀體會直角坐標系的思想，又通過方格紙研究幾何圖形的有關特點和性質，獲得幾何活動經驗，發展幾何觀念，逐步培養了學生推理的意識和能力。

根據學習《數學課程標準》所得及多年的實踐體會，小學數學的不少內容都有知識上的對應關系存在，所以教師應該利用對應思想來指導學與教。教師首先認識和利用數學對應思想，引導學生從數與實物、線、圖形、數量關系、空間等各元素之間產生的元素和元素的對應關系開始，由淺入深、由具體到抽象，逐步形成自己的數學對應思想與具有自覺用數學對應思想的思維品質，最終達到多種思維齊發展和夯實學生數學思維的目的。

（責編 藍 天）