構建高中數學本真課堂的實踐探索

●鄭日鋒

(學軍中學 浙江杭州 310012)

自國家新課程標準實施后，教師的教學觀發生了較大的改變，課堂教學行為也發生了一些改變，在全國、省、市的一些優質課評比或展示中可見一斑.但是“穿新鞋、走老路”的現象依然存在，許多教師在高考的指揮棒下，為了片面追求升學率，在數學課堂上滿堂灌，進行大容量教學，無視學生的認知規律，無視數學學科本質，無視教學的育人功能，停留在知識教學層面，導致許多學生喪失了學習興趣.許多教師把數學課堂簡單地看作“傳遞數學知識的地方”，教師講，學生聽，教師示范，學生模仿，學生一直以來在“模仿、練習、記憶、熟練”不斷循環中學習數學，導致許多學生認為數學是枯燥乏味的，討厭數學，懼怕數學.為了學生的終身發展，我們的教學既要指向當前，又要指向學生的未來，不能以透支學生的未來興趣為代價，改變這種“快餐式”的數學課堂教學，是時代的要求.構建本真的數學課堂，讓數學課堂成為具有師生生命意義的課堂，是當下每一位數學教師需要探索的課題.

1 對本真數學課堂的認識

所謂本真的數學課堂，就是遵循教與學的規律，實現學生、教師、文本、教學資源的交互作用，體現教師的主導與學生的主體，讓教學效果最大化.而構建本真數學課堂需要以下3個理論的支持.

1.1 基于學生發展的需要

數學對于人類理性精神的養成與發展有著特別重要的意義.數學學習使人類學到了一些處理問題的基本思想方法，有能力掌握相應的數學工具解決將來在專業工作中遇到的困難.

1.2 基于3個理解

理解數學.重數學本質的揭示與思維過程的暴露，重知識的發展過程與知識間的邏輯關系，重數學概念的理解與深化，重數學思想方法的提煉與總結.

理解教材.教師對教材的理解體現教者本色，對教材內容按教的視角進行重構，尊重教材而不盲從教材，從“教教材”到“用教材教”再到“創造性使用教材”.

理解教學.教學的藝術不在于傳授的本領，而在于激勵、喚醒和鼓舞.教師做學生學習的引導者，在學生已有的認識基礎上因勢利導，通過啟發、點撥，引領學生自然走到教師預設的方法中來，實現教與學的和諧統一.

1.3 基于意義學習

奧蘇貝爾在其提出的意義學習理論中指出，意義學習所必需的2個內部條件是：(1)學習者具有同化新材料的認知結構；(2)學習者具有學習新材料的學習心向.前者涉及教學的認知維度，即教材內容為學生可接受；后者則涉及教學的情感維度：教材內容為學生樂接受.前者是教材編寫者的主要任務，后者則是教師工作的藝術性體現——即怎么從學習形式上使得教材內容與學生更匹配.

2 構建本真數學課堂的教學實踐

本真的高中數學課堂，在追求教學特色的同時有哪些核心要素呢？筆者以案例的形式試圖探尋核心要素及其教學作用.

2.1 導

以境育情，促進學生迅速進入角色，引起學生的學習興趣或獲得情感上的共鳴，為順利展開教學作好鋪墊.

情境創設要著眼于：貼近學生的生活實際；有一定的思考價值；學生能感悟又蘊藏教材知識；體現時代精神；幫助學生建立數學概念、公理、公式、定理等數學模型，引發學生認知上的沖突，激發探究的熱情.

一堂成功的數學課，是從精彩的導入開始的，正如鄭毓信教授所指出的，情境設置不應該僅僅起到“敲門磚”的作用，還應當在課堂的進一步開展中自始自終發揮重要的向導作用.

案例1 指數函數的導入

現在將一張報紙反復進行對折，請學生們完成表1：

表1 對折x次后報紙的厚度和面積

學生完成表格后，教師給出以下問題：

(1)試寫出報紙厚度y與折紙次數x之間的函數關系式；

(2)試寫出報紙面積y與折紙次數x之間的函數關系式.

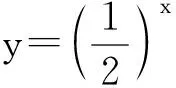
本教學片段從學生熟悉的折紙試驗出發，得到2個特殊的指數函數模型，這2個特殊的指數函數不是以前學過的函數類型，需要新命名，從而自然引出指數函數的定義.而且這2個特殊的函數分別代表“底數大于1的指數函數”與“底數大于0而小于1的指數函數”，為研究指數函數的性質埋下伏筆.

2.2 味

讓數學味充溢課堂，設置問題鏈，錘煉學生的數學思維，提高數學素質，需要教師上的每一節課都有1個中心——數學核心，以及2個基本點——教師的點撥與學生的領悟.

案例2 橢圓第1課時的教學片段

師：(完成了橢圓的定義教學后)剛才我們得到了橢圓的定義，怎樣才能更深刻地認識橢圓呢？

生1：建立橢圓的方程，利用橢圓方程研究橢圓的幾何性質.

師：很好！我們現在探究橢圓的標準方程.有哪些步驟？

生2：建—設—限—代—化—證.

在學生建立了如圖1所示的平面直角坐標系后，教師提出問題：前面我們通過幾何畫板，把圓變成橢圓，現在能否借助圓的方程類比猜想出橢圓的方程？

(先獨立思考，再小組交流.)

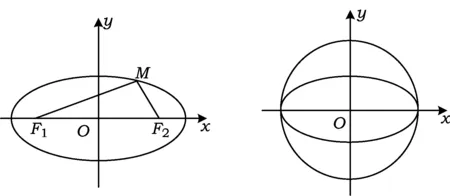
圖1 圖2

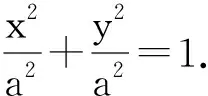
師：學生3利用類比推理及橢圓與圓的關系猜想橢圓的方程，猜想得到的結論是否正確？如果正確，需要給出嚴格的證明.

生：猜想正確，利用求曲線方程的方法給出證明.

(下略.)

本教學片段跳出常規教學的視角，從再創造教學的視角，啟發引導學生從以原點為圓心的圓方程，大膽猜想橢圓的標準方程，然后讓學生證明猜想，凸顯了數學的本質，讓數學課散發出濃郁的“數學味”；通過展現數學發現的過程，激發學生的創新意識；培養了學生的合情推理能力，把復雜的數學知識變得簡單明了.

2.3 奇

在中學數學教材中，有些章節的內容顯得比較淺顯，學生一看就懂，需要教師化平淡為奇妙，挖掘其中蘊含的豐富思想及數學意蘊；還有些章節概念深奧，大部分學生難以理解，需要教師化奇妙為平淡，搭建腳手架，基于符合學生認知水平進行教學設計.

案例3 古典概型的教學片段

出示問題：拋擲2枚質地均勻的硬幣，出現一正一反的概率是多少？

師：此問題的答案是多少？

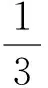
接著教師給出了2個試驗：

試驗1 拋擲一枚質地均勻的硬幣.

試驗2 拋擲一顆均勻的骰子.

首先引導學生建立古典概型這一重要的概率模型，并探索出古典概型中隨機事件的概率公式，再讓學生探討課前問題.

本教學案例中，古典概型對學生來說并不陌生，在初中教材中就接觸過，屬于學生一看就懂的內容.教師從一個具體問題的2個不同答案出發，引發認知沖突，激發學生的求知欲.因為要解決問題，所以需要建立數學模型，然后以2個試驗為載體，通過師生互動對話，不斷促進學生思考，讓學生經歷觀察、歸納、猜想、驗證的數學探究過程,體現“化平淡為奇妙”.

2.4 活

新課程倡導在教師主導下的學生自主學習的過程，這就要求在課堂教學設計中，教師要進行換位思考，想學生之所想，走進學生的數學學習心理，實現教師的所想與學生的所思“渾然一體”，師生的思維得到升華.

案例4 參數方程概念的教學片段

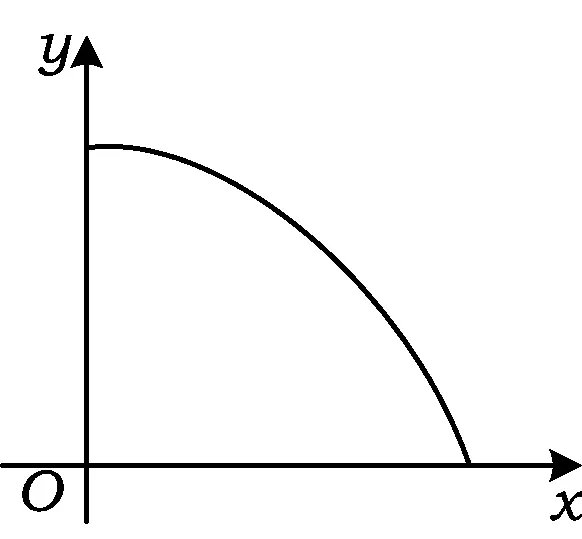
圖3

首先給出問題：假設“憤怒”的小鳥以初速度5 m/s水平拋出，小鳥距地面高度為1 m，取g=10 m/s2，你能提出什么問題？

生：(1)求小鳥到達地面的時間；(2)求小鳥運動的軌跡方程.

師：請同學們嘗試求小鳥運動的軌跡方程.

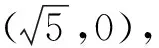
師：為什么是二次函數的圖像，還有其他方法嗎？

生2：小鳥的運動可以分解為：水平方向作勻速直線運動，豎直方向作自由落體運動.設在時刻t小鳥到達點M(x,y)，則

師：很好！你能否證明小鳥運動的軌跡是拋物線？

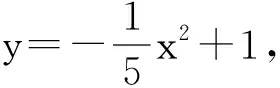
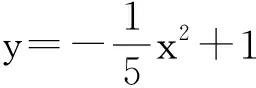
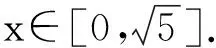
生2：t起了過渡作用.

師：我們把此方程組取個名字，叫做曲線的參數方程.今天我們就參數方程的意義作一些探討.

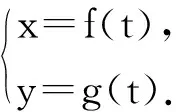
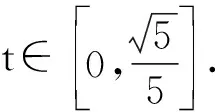
在本教學片段中，教師以憤怒的小鳥的運動軌跡引入課題，源于對運動的研究，學生對平拋運動是熟悉的，讓學生感悟到參數方程是拋物線的另一種形式，參數是媒介.教學過程中充分重視了知識的發生、發展過程，沒有把知識硬塞給學生，而是自然地、水到渠成地讓學生接受知識，并且讓學生經歷不斷地完善知識的過程，獲得情感上的共鳴，讓教師所想與學生所思“渾然一體”.

2.5 實

教師把自己置于困境中，并再現自己或數學家從中走出來的過程，讓學生看到教師或數學家的真實思維過程是怎樣的，讓數學思想隨著“數學知識”的“春風”潛入學生的腦海中.

案例5 二項式定理的教學片段

1664年冬，牛頓在研讀了沃利斯博士的《無窮算術》后思考：

(a+b)2=(a+b)(a+b)=a2+2ab+b2,

(a+b)3= (a+b)(a+b)(a+b)=

a3+3a2b+3ab2+b3,

(a+b)4= (a+b)(a+b)(a+b)(a+b)=

a4+4a3b+6a2b2+4ab3+b4，

對任意正整數n,(a+b)n有怎樣的結果呢？

請觀察(a+b)2,(a+b)3,(a+b)4的展開式，并思考：展開式中的項是如何得到的？展開式中各項的系數是如何確定的？你能猜想(a+b)n的展開式嗎？

本教學片段以牛頓的思考引發學生探究，讓學生感悟數學家思考問題的方法與角度，能激發學習的興趣及創造性.

2.6 疑

讓學生帶著作業的同時，能帶著問題依依不舍地走出課堂.

案例6 隨機變量的均值與方差習題課

問題1 一個口袋里裝有大小相同的3個紅球和2個黃球，從中任取2個，求其中含紅球個數X的均值與方差.

問題2 一個口袋里裝有大小相同的3個紅球和2個黃球，從中有放回地取球2次，求其中含紅球個數X的均值與方差.

課堂上解決了問題1和問題2后，教師提問：

(1)問題1中的X服從什么分布？(答案：超幾何分布.)

(2)問題2中的X服從什么分布？(答案：二項分布.)

(3)這里的超幾何分布與二項分布的均值相等，而方差不等，這是偶然的巧合嗎？

本教學片段通過布置課外探究式作業，將課堂知識向課外延伸，讓師生在自主、合作、探究中鍛煉思維，體驗求知的艱辛與快樂，實現教學的雙贏.

結束語 構建本真的高中數學課堂，旨在使數學課堂煥發活力，使課堂成為教師與學生共同成長的舞臺，打破數學課堂“千人一面”的現象，從學校層面，打造具有學校特色的課堂教學，從教師個體層面，打造具有個人特色的課堂.