習慣不一定自然 常理不一定合理
——記一道競賽不等式證明題的困惑與收獲

●江戰明

(德清縣高級中學 浙江德清 313200)

基本不等式在高中數學中的運用是廣泛的，意義是重大的，特別是在比較大小、最值問題和不等式證明中,其快捷、高效的實用價值更是不言而喻.正是由于基本不等式的“屢試不爽”，以致于當基本不等式運用失效時，總會給人一種“難以置信”的錯覺和“莫名”的困惑.下面以筆者親歷的一道不等式證明題為例，談談當基本不等式運用失效時，所采取的一些方法和措施，以期拋磚引玉，為不等式證明教學增添“色彩”.

1 案例呈現

在一次課外輔導后，有一名高二文科學生帶來了一道不等式證明題，她覺得她的證明已經比較“巧妙”了，但不知道為什么結果“正好”與結論相反，因此她感到很困惑.具體問題如下：

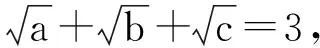
給出學生的證明如下：因為a,b,c>0，所以

2 案例分析

其實在上述證明過程中，縮小3個因式分母的想法“沒問題”，但用基本不等式逐個去縮小分母，確實會因為過度放大而導致證明無法完成，這意味著光靠基本不等式難以完成證明，需另辟蹊徑.

3 案例研究

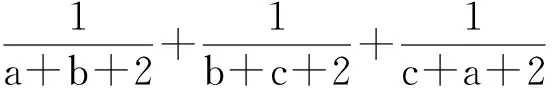
為了計算方便，把例1改寫為：已知a,b,c∈R+，a+b+c=3，求證：

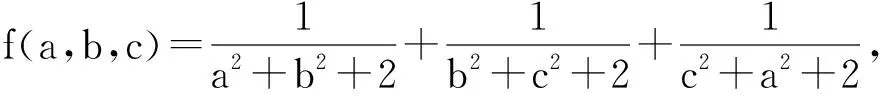
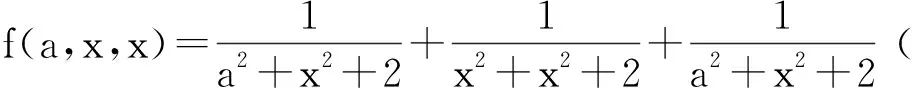
因為a≥b≥c>0,a+b+c=3,所以abc≤1，bc≤1，即4-4bc≥0，2a2-b2-c2≥0，從而f(a,x,x)-f(a,b,c)≥0成立，即f(a,b,c)≤f(a,x,x).

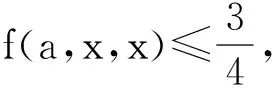
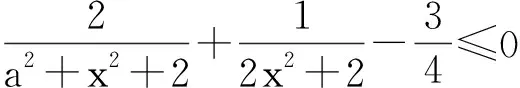
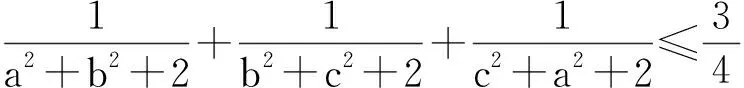
至此，問題終于得到了解決，但如此“有悖常理”的方法、如此復雜的計算，怎樣去向高二文科學生解釋呢？是否還有其他更為簡單、自然的解法呢?于是筆者繼續進行研究并查閱相關資料，終于功夫不負有心人，在茫茫題海中發現2011年浙江省高中數學競賽附加試題的最后一題與本題相似．

下面給出原題及初等解法.

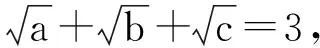
(2011年浙江省高中數學競賽第22題)

成立，顯然當a=b=c=1時等號成立.