例談“學為中心”理念下自主課堂的教學設計

●方云兵 陳美英

(浙江師范大學婺州外國語學校 浙江金華 321025)

現代教學論認為，教學過程歸根到底是如何教會學生學習.“學為中心”的數學課堂就是把學生學習作為教學中心，以學生自主學習、自主思考解決問題為主要學習形式，通過教師啟發學生思考達到深入理解數學的一種教學形式.“學生怎樣學，怎樣引導學生學，怎樣幫助學生學”是“學為中心”的精髓.本文試著從“三理解”的角度,即：理解教材、理解學生、理解數學的角度，通過3個教學設計的案例談談自己的一些做法.

1 理解教材——關注“怎樣引導學生學”

在對教材進行分析時，堅持宏觀把握教材、微觀分析教材，樹立“整體教材觀”，既要分析教學內容所在節的教材處理、理解章前圖的內涵，又要看到這部分內容在整章中的地位和作用，甚至各種版本教材對這節內容的處理，這樣就能從整體上理解本節內容，更深入理解教材對于這部分內容及其相關內容的編寫意圖.首先要理解教學內容，弄清“是什么”，明確例題的地位和作用，弄清習題與例題的關系，揣摩插圖的編排意圖，鉆研提示語和旁注；其次要理解教材整體結構及前后關系，在概念體系中認識核心概念；最后要理解教學內容所反映的思想方法.在依托教材的基礎上，根據實際需要把教材內容通過問題的形式，對學生的有效思考進行啟發，最大程度地發揮教材的功能，把著力點放在“怎樣引導學生學”上.

案例1 “嘗試檢驗法”的教學設計(浙教版七年級上冊第5.1節“一元一次方程”)：

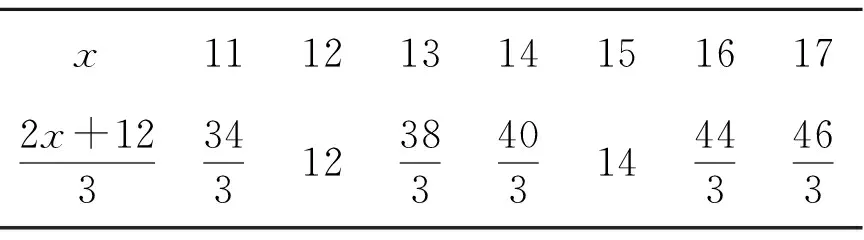
表1 代數式對應值

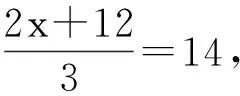
教材的設計本意是銜接合作學習問題(3)(小強、小杰、張明參加投籃比賽，每人投了20次．小強投進10個球，小杰比張明多投進2個，3個人平均每人投進14個球．問小杰和張明各投進多少個).但是在實際教學過程中，絕大多數學生都是采用小學所學的逆運算的方法解方程(班級44位學生，只有10位學生采用嘗試檢驗).學生們很困惑，明明可以用小學的逆運算解簡單方程的方法直接求解，為什么要這么復雜進行嘗試檢驗呢？這樣的教學設計重教材、輕學生；重接受、輕理解；重結果、輕過程.在教學時教師講到為止，學生聽到為止，速戰速決，思想過程匆匆而來又匆匆而去，學生就囫圇吞棗地接受了，而沒有進行思想方法的引導.學生對方程解的探究過程帶有一定的盲目性，完成不了知識內容的內化和數學經驗的積累，更沒有從質和量上豐富原有的思想方法.

設計改進 在上一環節讓學生自學判斷t=3是不是方程3t+1=7的解后思考：剛才我們在計算時發現，t=3不是原方程的解，那么方程的解是比3大還是比3小？你是怎么想的？

生：當t=3時，左邊=10，比右邊大，說明取值太大了，應取比3小的數.

師：你會試著取幾？

生：取t=2.

師：按照剛才總結的判斷一個未知數的值是否為一元一次方程的解的方法和程序(代、算、比、判)，試一試.

這種求一元一次方程解的方法叫做嘗試檢驗法！

設計意圖 通過這一環節完成從“一元一次方程的解”教學環節過渡到“嘗試檢驗法解方程”，讓學生的思維有一個順勢而上的過程.

然后指導學生閱讀教材內容，思考以下問題：

師：x必須是整數嗎？

生：因為進球數不可能是小數，所以肯定都是整數.

師：通過分析，方程解的范圍縮小了！

師：x可以取21，20嗎？

生：21不行，因為題目要求每人投20次.20也不行，如果是20的話，小杰就投了22次了，不符合題意.

師：通過分析，未知數的范圍又縮小了！

此時，教師又追問：x可以取9，10嗎？

生：不可以，因為平均數是14，小強只投進了10個球，另外2個人要比他投得多，平均數才會到14.

教師和學生一起歸納：嘗試檢驗法的一般步驟(略).

設計意圖 通過4個問題迫使學生不斷思考未知數取值的方法，體驗嘗試未知數取值的縮小過程.

跟蹤練習 對于方程3x-8=x，表2已給出部分未知數的值,請回答下列問題．

表2 方程對應值

(1)表2中a=______,b=______，思考：方程的解應在哪2個整數之間？

(2)寫出方程3x-8=x的解.

設計意圖 嘗試檢驗法是這節課的難點，筆者在處理時，增添教學環節間的過渡，深挖學生閱讀文本時容易“滑過”之處，設計啟發學生深度思考的問題，通過不斷追問，順著人們的認知規律把判斷一個未知數的值和嘗試檢驗法這2個知識點自然地銜接在一起.重新編制嘗試檢驗法的教學素材，由于教材例題中的數都是整數，給學生造成不科學的嘗試路徑，這又是本節課的一個難點，于是教師改編了上面的跟蹤練習，其目的是：使學生體會逐漸逼近的思想，把單純地填表格(代數式求值)變為開放地思考；使學生明白嘗試取值時，既可以是正數，也可以是負數，還可以是小數.這樣既加強了對未知數取值的學法指導，又引導學生對學習信息進行整理歸納,使學生完整經歷嘗試檢驗、嘗試取值的過程.

2 理解學生——關注“學生怎樣學”

在課堂教學中要始終堅持以學為中心，從學生的認知水平出發，以學定“問”，充分考慮學生已有的經驗、學習基礎、思維特點，立足于學生的“最近發展區”，用學生的眼睛看數學，由感性到理性、由淺入深地設計問題，真正引導和幫助學生思考問題、分析問題和解決問題.

案例2 九年級上冊第1.1節“反比例函數概念”鞏固問題設計(案例來源：浙江省金華市開發區優質課評比).

1.下列函數中,y是x的反比例函數嗎？如果是，比例系數k是多少？

2.辨析題:兄弟2個人分吃1碗餃子，每人吃餃子的個數如表3所示:

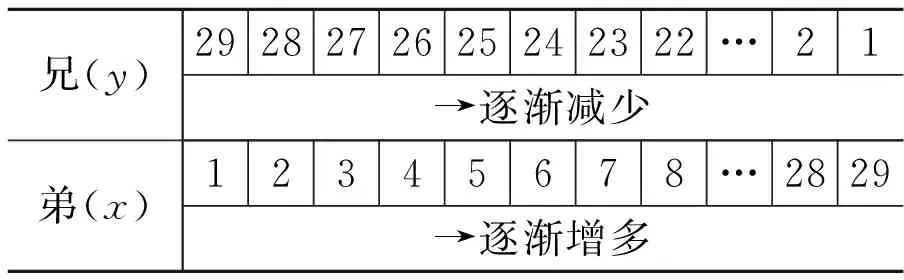
表3 每人吃餃子的個數

(1)寫出兄吃的餃子個數y與弟吃的餃子個數x之間的函數關系式(不要求寫x，y的取值范圍)；

(2)因為當弟吃的餃子個數x增多時，兄吃的餃子個數y在減少，所以y與x成反比例,你認為對嗎？說說你是怎么想的.

3.y是x的反比例函數，表4給出了x與y的一些值:

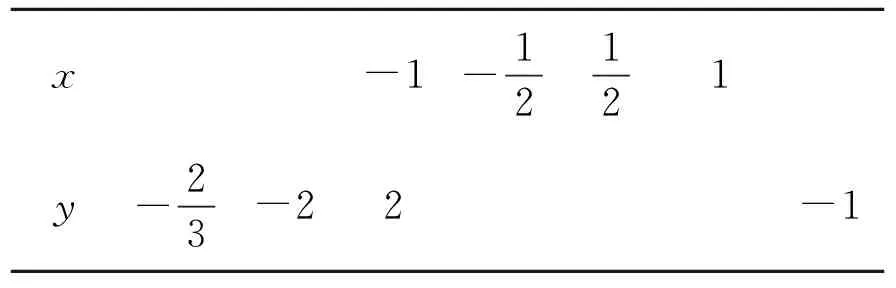
表4 x與y的對應值

(1)寫出這個反比例函數的表達式;

(2)根據表達式完成表4.

教師通過設計2個練習暗含反比例函數的2種表示方式(解析式法、表格法)，使學生在辨析中深刻理解反比例函數的本質.在鞏固練習2中，把學生存在的疑點、易混點呈現給學生.從字面上理解“反比例”，學生就有“增大而減小”這一首印象，再加上學生受小學所學和七年級科學相關知識中的成反比例關系的負遷移的影響，認為只要一個量增加、一個量減少就是反比例函數，特別是表3中的“逐漸增大”與“逐漸減少”更有迷惑性.這樣設計的優點是通過學生的活躍爭執以理服人，最后回到反比例函數的概念上，達到“理越辯越明”的教學效果.這個過程真正做到了“學為中心”，既關注結果，更關注過程.列表法本身也是函數的3種形式之一.設計表格的形式，把反比例函數的解析式隱藏在表格中，先判斷比例系數k，然后再求其余自變量和因變量的值，灌輸了“待定系數法”的數學思想.

3 理解數學——關注“怎樣幫助學生學”

理解數學是教好數學的前提.教師“理解數學”的目的是讓學生“理解數學”，這也是教學的首要任務.讓學生能“理解數學”主要通過課堂教學來完成，而進行課堂教學的效果要依托于教學設計.從課堂本身出發，教師更應重視教學設計，使教學設計的落腳點放在“怎樣幫助學生學”，關注:學生學習這一知識點的起點是什么？難點在哪里？怎樣突破難點？怎樣把復雜的問題通過層次設計使學生比較容易理解，理解深刻?

案例3 二元一次方程組解法1(案例來源:浙江省金華市三區教研活動公開課).

(1)

(2)

學生嘗試解答后,教師請學生口答解題過程.

生1：把式(2)代入式(1)得y=3，代入式(2)得x=1.

師：你們和他的答案一樣嗎？

生(全體)：一樣！

師：為什么把式(2)代入式(1)呀？為什么把y=3代入式(2)而不代入式(1)？

生2：這樣可以直接求出x，更簡單.

師：怎樣檢驗？

生3：代入方程組中的每一個方程,看方程2邊是否相等.

師：例1的解題步驟是什么？先做什么？再做什么？

生4：代入消元→回代求解→檢驗作答.

師：還有哪些注意點？

生5：整體代入時要添加括號、最后要檢驗.

本節課的核心思想是消元與轉化，除此之外，還涉及到程序化思想和簡化、優化思想，在教學中也應注意適度滲透.同時教師還應時刻在課堂中把基本的數學思想方法與知識、技能融于一體，使學生在學習知識、技能的同時領悟到一定的數學思想方法，在運用思想方法的同時鞏固知識、技能，這樣，思想方法就有了載體，知識技能就有了靈魂，真正做到“學為中心”的課堂.鑒于以上認識，筆者對本環節進行了如下改進：

講解例題后，變式練習：

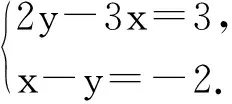
(1)如何把方程組轉化為一元一次方程？怎樣轉化比較簡便？

(2)哪個未知數的值可以先求出來？從哪里入手？問題解完了嗎？

(3)另一個未知數的值如何求？

(4)可以把x=y-2代回x-y=-2求解嗎？為什么？

(5)先求出的一個未知數的值可以代回到方程組中，求出另一個未知數的值嗎？代入哪個更簡單？

(6)你能總結代入法解二元一次方程組的一般步驟嗎？

代入消元法解二元一次方程組的基本步驟如圖1所示：

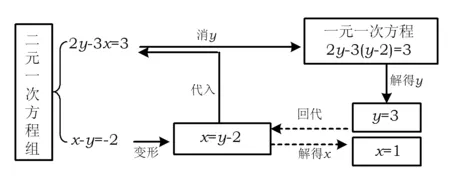
圖1

程序化解法也有消極的一面,它使運算成為一種機械操作.可能出現的情況是：學生遇到特定的情景，就機械地套用代入法的一般步驟；面對三元一次方程組時更是感到束手無策.

對問題的設置改進如下：

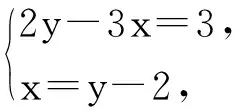
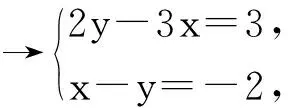
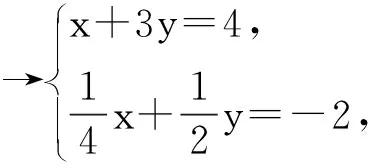
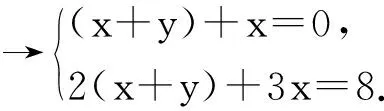
解二元一次方程組的本質是消元，即把“二元”轉化為一元.消元的基本方法是代入法、加減法，這2種方法的本質差別在消元的具體步驟上.代入消元先要將其中一個二元一次方程變形成用一個未知數的代數式表示另一個未知數的形式.變形的基礎是等式的基本性質，這一步變形也是學習一次函數內容必備的基礎，因此這種變形能力對學生后續的學習非常重要.加減消元法的本質內涵是整體思想，學生先利用等式的性質把2個方程中其中一個未知數的系數變成相同，這樣整體加減時，才能達到消元的目的.加減消元中的整體思想是數學中常用的思想方法.從2種解法的運算程序和推理步驟看，代入消元法更具通性，加減消元法側重于方程變形的技巧，因此教材安排2個課時讓學生先學習代入法，再學習加減法.通過這樣的設計改進，幫助學生理解解二元一次方程組的通性通法，真正打造“學為中心”的成長課堂.

每個學生的學習品質存在差異，對數學的理解存在差異，而教材的重、難點是教學的重心所在，是學生認知矛盾的焦點，也是學生學習的困惑點.學習是新知識的生長過程，學生在學習的過程中往往會遇到思維的障礙.“學為中心”的成長課堂要求學生在閱讀課本中的概念、定理等文本內容以后，幫助學生深入理解概念的內涵或定理的條件、結論而設置問題，面對不同層次的學生，使不同的學生思有所得、思有所悟.立足于學生“最近發展區”的問題串設計給學生搭建起“適切”的“腳手架”，由淺入深，環環相扣，層次遞進，形成了一條完整的問題鏈，滿足了不同層次的學生需求，幫助學生思考問題、分析問題，突破了學困點.

從教為中心到學為中心，是從研究怎樣教，到研究怎樣學，即怎樣引導學生學、怎樣幫助學生學的過程；是讓學生嘗試自主學習，主動獲取知識的過程；是生生合作、小組交流的進一步升華.“學為中心”的成長課堂，要求教師變“規定描述”為“引導建構”，教學設計要找準知識的生長點，重學生感悟；變“列舉告知”為“辨析發現”;要能拓展知識的“延伸點”，重教師引悟；變“真題訓練”為“內化匹配”;要能突破學生的學困點，重學生頓悟.

[1] 李海東.理解數學是教好數學的前提——“中學數學核心概念、思想方法結構體系及其教學設計的理論與實踐”初中第五次課題會議成果綜述[J].中學數學教育，2010(4)：1-4.

[2] 向慧英，李家寶.聯系實際巧設計 生成新知見實效——反比例函數的定義的教學實錄及評析[J].中學數學教育，2011(12):22-26.[3] 徐曉紅.問題設計應基于理解[J].中學數學教學參考：中旬，2012(1/2):25-27.

[4] 楊紅芳.殊途能否同歸——兩節同課異構案例引發的思考[J].中小學數學：初中版，2011(11)：33-35.