一題多解背后的形式化思考

●洪昌強 陳淑麗

(臺州市第一中學(xué) 浙江臺州 318000)

解題是數(shù)學(xué)學(xué)習(xí)的重要活動之一.在解題教學(xué)中，教師經(jīng)常給學(xué)生提供較多的解題方法，試圖通過一題多解，提高學(xué)生的解題能力，激發(fā)數(shù)學(xué)學(xué)習(xí)的興趣.但往往事與愿違，教師的好意學(xué)生不但不領(lǐng)情，反而常常聽到一些學(xué)生的抱怨：“這么多種方法，我都不知道該用哪一種，方法越多反而解題思路越混亂.”學(xué)生的抱怨值得反思：為什么教師提供多種解法反而造成茫然的感覺？在解題的教學(xué)中，是否僅僅是為了“多解”而“多解”?是否缺乏必要的反思和系統(tǒng)化的過程？人教A版《數(shù)學(xué)(必修4)》(以下簡稱教科書)導(dǎo)引所言：學(xué)習(xí)始于疑問,學(xué)而不思則罔.筆者以2013年浙江省數(shù)學(xué)高考理科第6題為例，談?wù)剬σ活}多解的一些思考.

( )

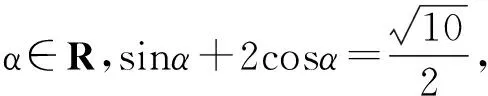
1 探索不同的解法

解法1 原式2邊平方，得

由橢圓的定義得

則

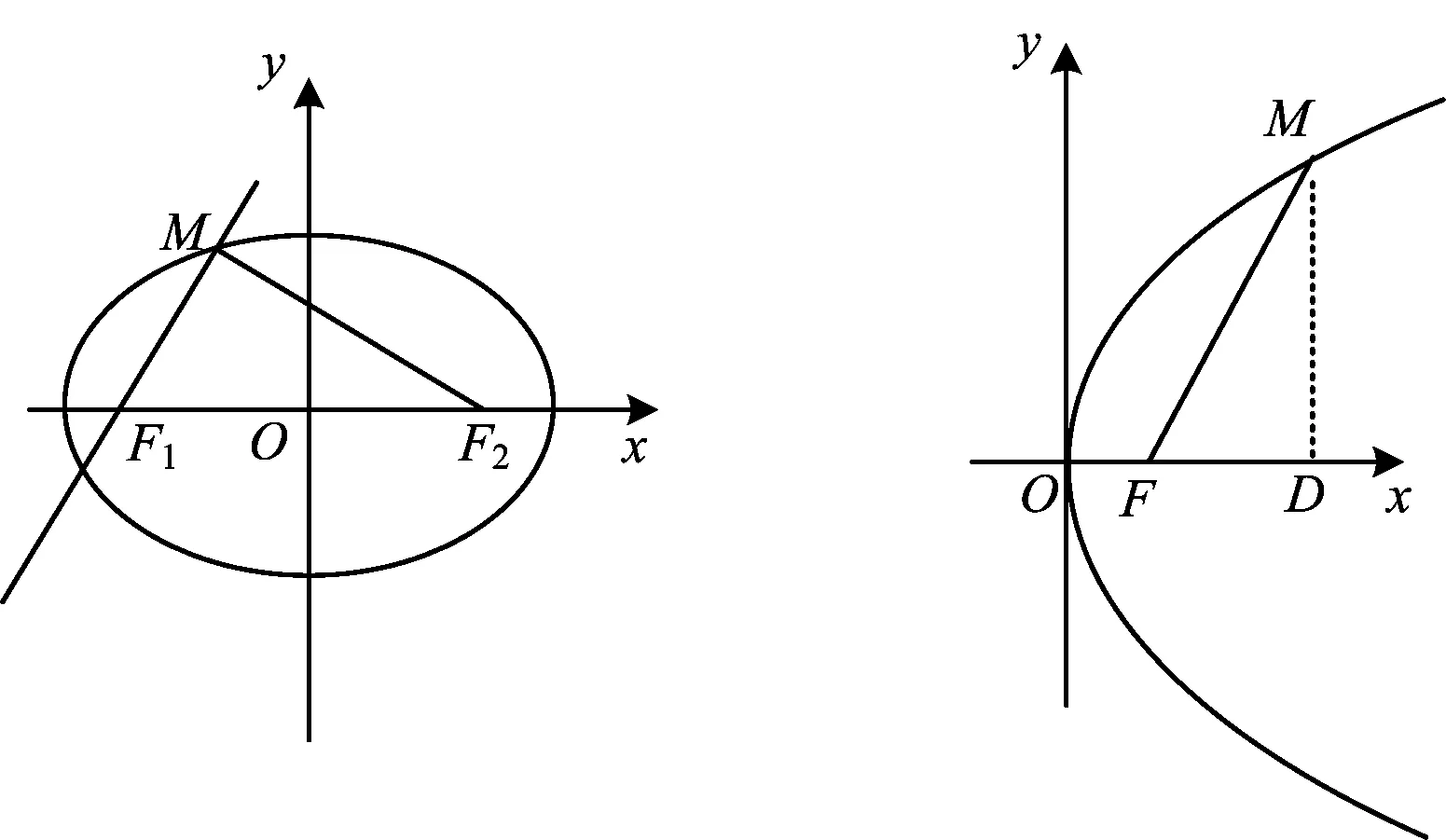
圖5 圖6

解法5 如圖6，由拋物線y2=4x知F(1,0)，|KF|=p=2，過點M作MD⊥x軸，垂足為D.設(shè)|MF|=d,則

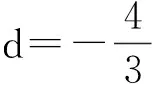
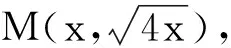
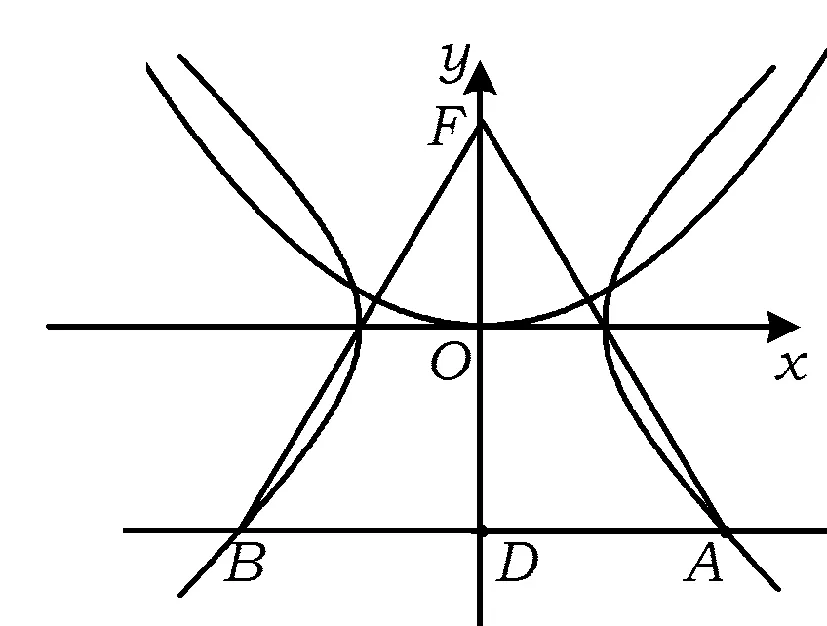
圖7

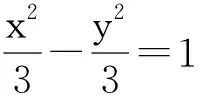
(2013年江西省數(shù)學(xué)高考試題)

由圖7可知

即

解得

p=6.

3cos2α+4sin2α=0,

則

解法2 原式2邊平方，得

3tan2α-8tanα-3=0，

解得

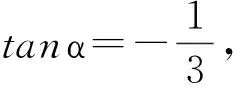
從而

解法3 先移項，再2邊平方，解得

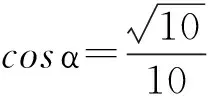
下略.

解法4 原式化簡為

得

解法5 設(shè)x=cosα，y=sinα,由

得

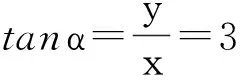
下略.

解法6 對于解法5的方程組也可以從解析幾何角度去審視.

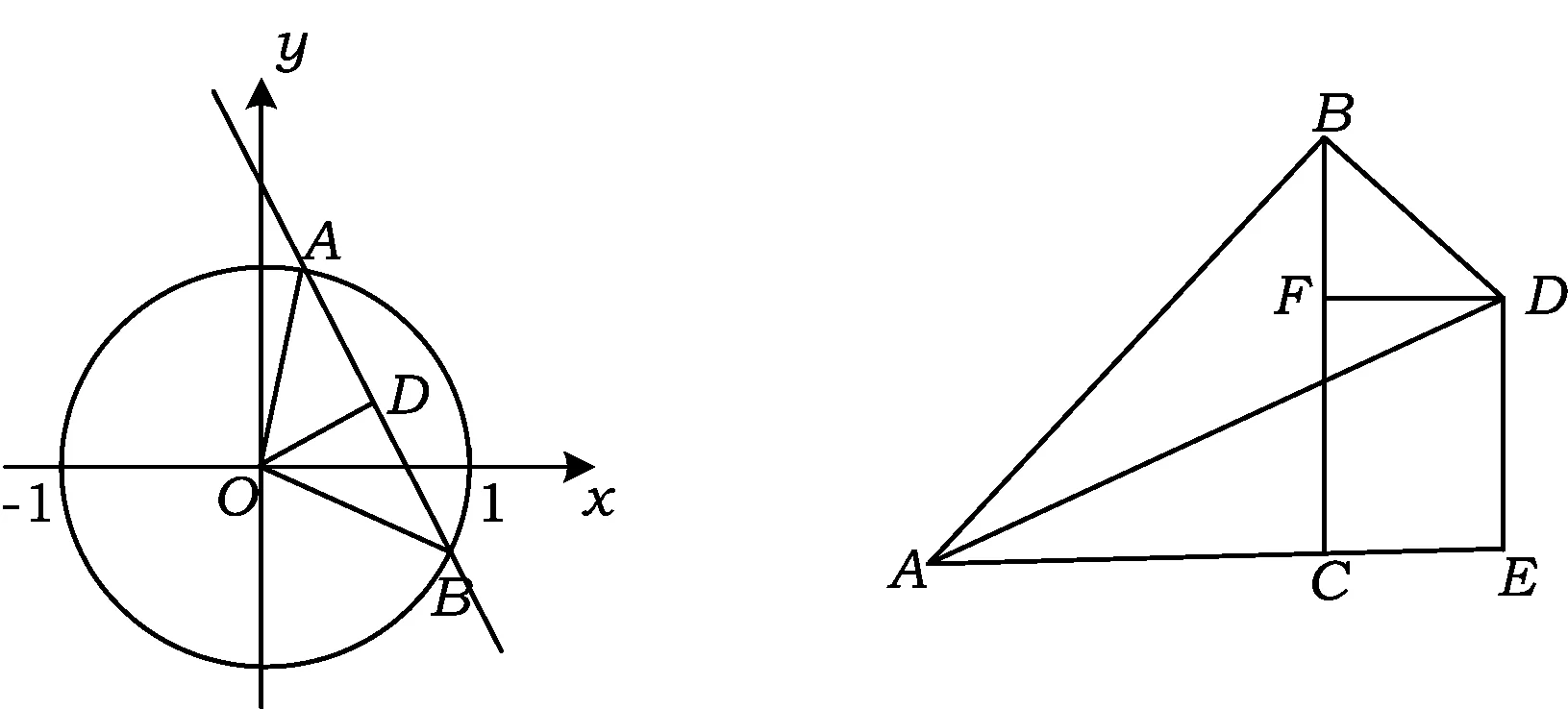
圖1 圖2

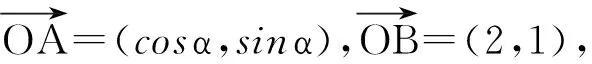
從而

解法8 當(dāng)α為銳角時，如圖2，作Rt△ABD,其中∠ABD=90°,AB=2,BD=1,再作∠BAE=α,過點B作BC⊥AE,垂足為C,過點D作DE⊥AE,垂足為E,過點D作DF⊥BC,垂足為F,則

∠DBF=α,

從而AE=AC+CE=AC+DF=

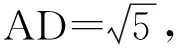
2 比較方法的異同

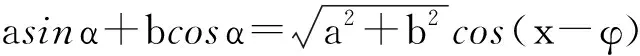
以上各種解法涉及到兩角差的正(余)弦公式、同角三角函數(shù)關(guān)系式、向量的數(shù)量積、點到直線距離公式及勾股定理等知識.這些涉及到三角函數(shù)、解析幾何、向量、平面幾何等不同板塊的不同解法，貌似沒有什么聯(lián)系，其實在這些知識背后都存在著邏輯聯(lián)系.

3 探究知識間的聯(lián)系

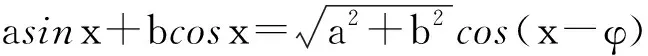
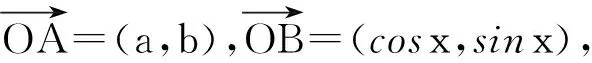
對于解法6，在單位圓中利用了點到直線之間的距離公式及直線斜率等知識，其中點到直線距離公式發(fā)揮了重要作用.那么，點到直線的距離公式能否由向量數(shù)量積導(dǎo)出呢？

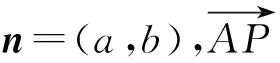
又因為

所以

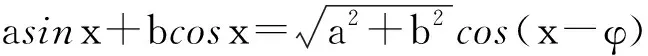
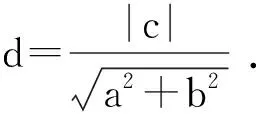
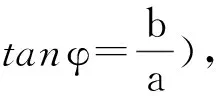
所以

即

3.3 方法簡捷的根源在哪

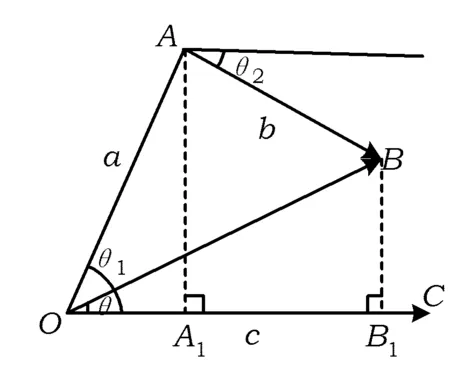
圖3

4 不該停止的思考

看似平淡的一道題，但平淡背后卻蘊含著火熱的思考.在解題的教學(xué)中,不能只停留在找到答案或得到泛泛的解題方法之上.教師必須站在更高的層面，以更寬的視野、更理性的眼光去思考數(shù)學(xué)問題、領(lǐng)悟數(shù)學(xué)哲理，然后引導(dǎo)學(xué)生對各種解題方法進行差異比較，追根求源.通過對問題的不斷深入思考,讓學(xué)生的思維觸角從一題多解的背后延伸到臺前,從而對數(shù)學(xué)知識的來龍去脈看得更清、把握更準,最終讓學(xué)生站得更高、走得更遠.