好一道令人深思的奇函數試題
——對一道高三教學調研試題的研究

●袁智斌

(深圳外國語學校 廣東深圳 518083)

函數、奇函數等知識，既是高中數學教學的重點內容，又是學生學習中的難點．如何把握這些重點內容的教學并幫助學生突破這些難點？筆者認為既要開展“開口動腦記公式、悟其結構巧解題”[1]的數學知識和方法發生、發展的過程教學；又要在“以問題為中心”的解題分析過程中有效地滲透數學思想方法，進一步促進學生對數學知識和方法的深入學習和深刻理解．

本文通過筆者所任教學校高三數學調研卷上的一道奇函數填空試題的研究，指出該題的參考答案存在的錯誤，并結合此題的分析與解答來解析奇函數的定義，促進學生理解奇函數的本質．

1 答案對嗎

原參考答案為：{0}或{-1,1}．

題目中“求函數定義域”的提法對嗎？另外，此題給出的原參考答案對嗎？首先，來看一下教材給出的函數定義：

一般地，設A,B是2個非空的數集，如果按某種對應法則f，對于集合A中的每一個元素x，在集合B中都有唯一的元素y和它對應，這樣的對應叫做從A到B的一個函數，通常記為y=f(x),x∈A.其中，所有的輸入值x組成的集合A叫做函數y=f(x)的定義域．給定函數時要指明函數的定義域．

從此定義出發，函數的先決條件之一就是必須先有“A,B這2個非空數集”以及某種確定的對應法則f，并且只有在它們滿足了“如果按某種對應法則f，對于集合A中的每一個元素x，在集合B中都有唯一的元素y和它對應”的條件下，“這樣的對應叫做從A到B的一個函數”． 由此得出，函數的定義域是和函數“與生俱來”的，從而不能籠統地說對函數求定義域．也就是說在廣義的情況下，泛泛地來談“求函數的定義域”是一個偽命題．

華南師范大學的沈文淮教授多年前在講課中提出過類似的觀點[2]．筆者重提此點，主要是呼吁大家重新來審視平時教學中一些習以為常但又存在不足或不當之處的教學觀點、提法和做法，以便進行改進，從而更好地發揚其優點．

其次，在默認“對于解析式表示的函數，如果沒有指明定義域，那么就認為函數的定義域是使函數表達式有意義的輸入值的集合”的情況下，此題的原參考答案完整嗎？

2 分析與解答

我們首先明確奇函數的定義：

一般地，如果對于函數f(x)定義域內的任意一個x，都有f(-x)=-f(x),那么函數y=f(x)是奇函數．

1-x2≥0，

解得

-1≤x≤1，

因此，f(x)的定義域D必須滿足D?[-1,1]，下面對D進行分類討論：

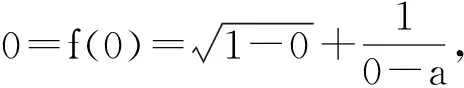
(其中常數a=1，定義域為D1?[-1,1))．

?x∈D1,由0=f(-x)+f(x)得

解得

x=0∈[-1,1).

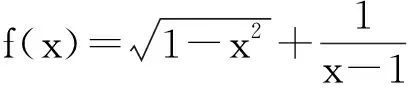
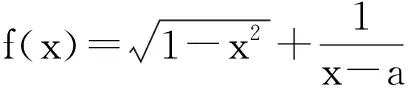
奇函數的定義蘊含著一個函數是奇函數的先決條件：函數的定義域D(φ?D)非空且關于原點對稱，即：若?x∈D，則-x∈D.因此，在任意取定x1∈D2?[-1,0)∪(0,1]后，該函數的定義域D2?[-1,0)∪(0,1]中將對應地存在一個-x1∈D2?[-1,0)∪(0,1].由題設條件知

0=f(-x1)+f(x1),

從而

(?x1∈[-1,0)∪(0,1]且x1≠±a).

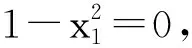
(其中a=0,定義域D2?[-1,0)∪(0,1]).

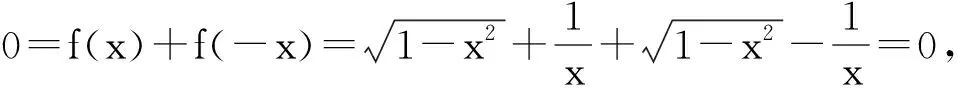
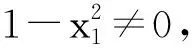
從而

(?x1∈(-1,0)∪(0,1)且x1≠±a).

由此可知，原參考答案的解答過程與結論不完整，遺漏了滿足題意的定義域

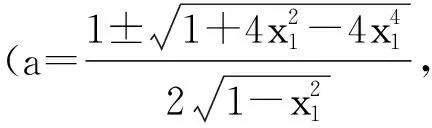
同時，原參考答案在表述上未準確反映出相應a的值，應在已求出的2個定義域“{0}或{-1,1}”的表述中及時補充相應參數a的值．

3 追問

在此，筆者提出以下問題進一步探尋：

答案也是否定的．原因在于：若假設D中存在2k+1(k∈N*)個元素，則由奇函數定義域的對稱性，可知0∈D.當0∈D時的情形前面已討論，得到D1={0}(其中a=1)，這與假設矛盾．因此，當D為有限集時，D中元素的個數不能為大于1的奇數．

問題3和問題4留給有興趣的讀者研究．

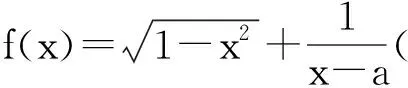
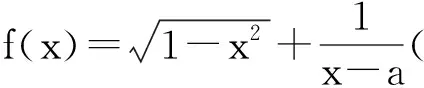
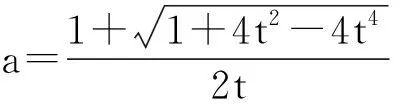
若a≤-1，則g(0)>0，g(1)>0，且g′(t)=3t2+a2-1≥0 (t∈[0，1])，從而g(t)在[0，1]上無零點，即所求定義域為空集,這與函數的定義域非空矛盾．

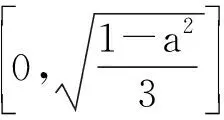
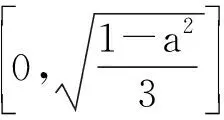
4 建議

其一，該題原參考答案的解答不完整從一個側面折射出奇函數等重點、難點知識在教與學的方式、方法上有待于改進與深化．數學教學中應該注重探尋數學知識、方法的教學與數學解題能力培養之間的內在聯系與關系，并通過科學地開展數學知識方法的深入教學來更加科學、高效地促進學生解題能力的提高．

其二，建議在今后新修訂的《普通高中數學課程標準(實驗稿)》、新版教材和試卷等，可將“求函數的定義域”修改為：求使函數解析式有意義的自變量的取值范圍．

其三，建議教師在平時教學中要注意自覺遵循波利亞在《怎樣解題》中提出的“回到定義上去”的諄諄教導，從而更加科學、有效、自如地開展教學、啟迪學生．

其四，該題不宜編排在高三教學調研卷的填空題處，更不宜編排在文科數學調研卷上的填空題處．若安排在高三文、理科數學卷的解答題部分，則將會更加彰顯此題的價值和功能．

[1] 陳都，王玉清，舒敬華，等.數學娛樂圈[J]．數學通訊，2004(17)：49．

[2] 袁智斌．系統扎實的研究生教育令我們受益終生[J].中學數學研究，2007(4)：15-17.

[3] 謝邦杰．抽象代數學[M]．上海：上海科學技術出版社，1982．

[4] 華東師范大學數學系．數學分析(下冊)[M]．北京：高等教育出版社，1981．