復數域中兩類函數的單值分支問題

馮 志 新

(吉林師范大學 數學學院，吉林 四平 136000)

復數域中兩類函數的單值分支問題

馮 志 新

(吉林師范大學 數學學院，吉林 四平 136000)

針對不同多值函數，分別運用限制輻角法和連續變化法系統地研究了對數函數與根式函數的單值分支問題.

多值函數；輻角；函數改變量；單值分支

初等多值函數是復變函數論中初等函數部分的一個重要內容[1]，其解析性質和映射性質要比初等單值函數復雜得多，研究的思想方法也比較獨特，學生不易理解和掌握，從而這部分內容成為該課程教學的一個難點．復變函數的解析性是以極限、連續、可微作為基礎，而這些概念都是針對單值函數來說的，因此無法在原來的意義下研究多值函數的解析性．在實際應用中遇到多值函數時也只是取它的一個確定的值，因此研究多值函數的根本方法是把多值函數分解為單值函數來研究，即通過特殊的方法把初等多值函數分解為若干單值分支，進而再研究每個單值分支的連續性、解析性等性質．

對于初等多值函數，引起其多值性的主要原因是輻角的多值性，針對比較簡單的多值函數，如根式函數、對數函數Lnz用“限制輻角法”將其分解為單值函數比較簡單，比較復雜的一般根式函數和一般對數函數LnR(z) 用“連續變化法”分解(其中R(z)為有理函數)．

1 根式函數w= (n是＞1的整數)的可單值分支問題

用限制輻角的方法確定其單值分支，步驟如下：

限制輻角：令0≤ ar gz＜ 2π(或 -π＜ argz≤π)

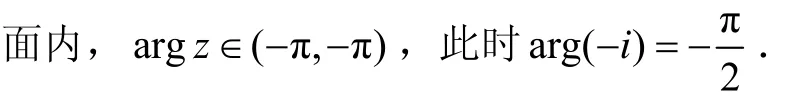
2 一般根式函數）與一般對數函數 LnR（ z）的可單值分支問題

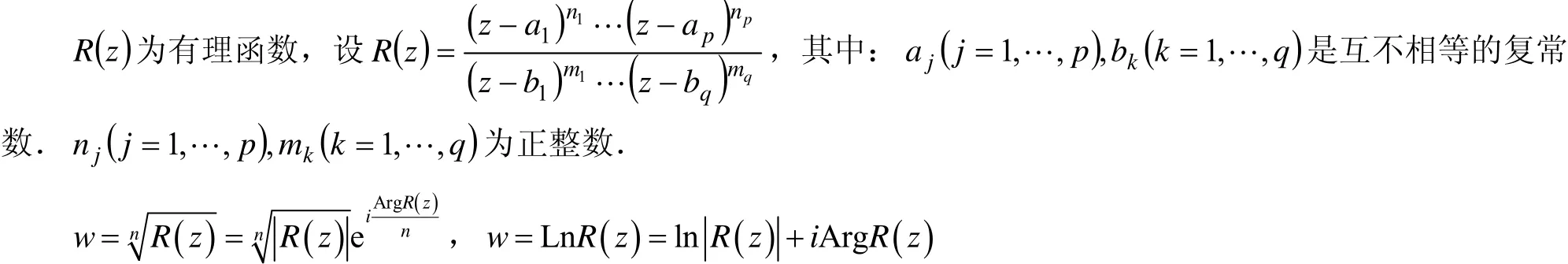
顯然這兩個多值函數的多值性是由 ArgR（z） 的多值性引起的，因此先研究ArgR（z）的可單值分支問題．而函數 ArgR（z） 比 Argz要復雜得多，繼續用限制輻角法研究很困難，利用函數改變量研究起來思路清晰，比較容易理解．

2.1 ArgR（ z）的可單值分支問題

用簡單曲線l適當地連接各支點，沿l割開z平面得到的區域D就是ArgR（z）的可單值分支區域．

ArgR（z）可單值分支的確定:設D是 ArgR（z） 的可單值分支區域z0∈D，初值?0=argR（z0）．對于?z∈D，在D內任意作一條連接z0,z的簡單曲線L，ΔLArgR（z）= argR（z） - argR（z0），故f（z） = argR（z）= ΔLArgR（z） +?0，稱其為由初值?0確定的單值分支．

2.2 LnR（ z）的可單值分支問題

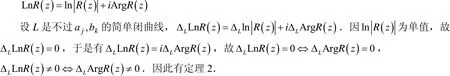
定理2LnR（z） 的支點與正常點和 ArgR（z）相同．

故 LnR（z） 的可單值分支區域與 ArgR（z）的可單值分支區域作法相同．

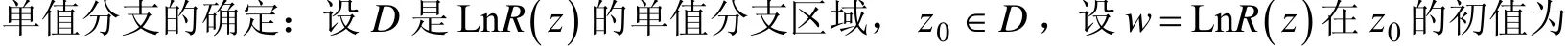
例2 求函數w=Ln（ 1-z2）的一個可單值分支區域，并求當z=0時取值為零的分支在z=2點的值．

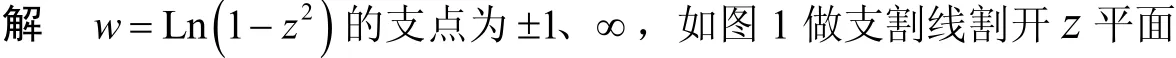
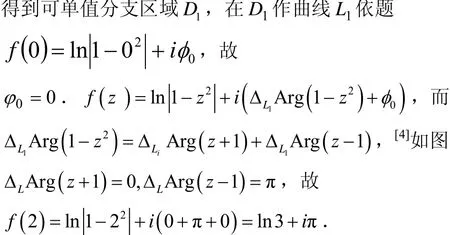
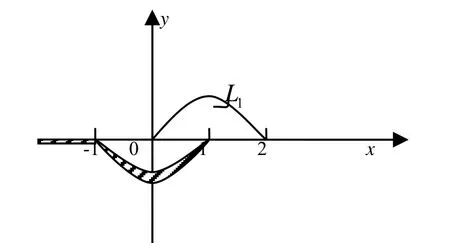
圖1 w=Ln（1- z2）的可單值分支區域

2.3 w=）的可單值分支問題

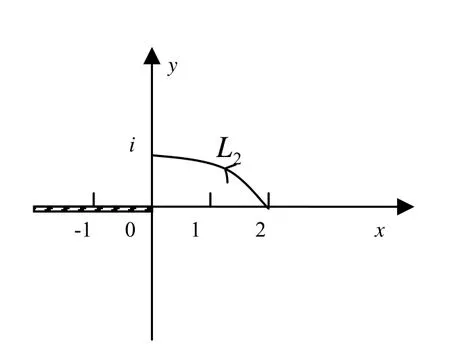
圖2 w=的可單值分支區域

用連續變化法研究多值函數的單值分支問題時需要注意的是，支割線應盡量選取一條最簡單的連接所有支點的曲線，特殊情況也可選多條，同時所作支割線要避開題中給出的已知點(起點)和要求的點(終點)，因為這兩點應該是在可單值分支區域內的，有時也在邊界上岸或下岸；在可單值分支區域內作簡單曲線連接起點和終點，因此這條簡單曲線不能和支割線有交點．

容易看出和 Lnz分別是和 LnR（z）的特殊情況，也可用連續變化法求解，根據定理1和定理3，和 Lnz的支點都為 0,∞ ，因此任意一條連接0,∞的簡單曲線都是支割線，但其中最簡單的就是正實軸或負實軸，可見還是限制輻角法比較簡單．

[1] 韓惠麗,房彥兵.多值函數在復變函數中的應用[J].大學數學,2007,23(4):180-183.

[2] 鐘玉泉.復變函數論[M].北京:高等教育出版社,2004:64-87.

[3] 劉聲華,宮子吉,沈永祥.初等解析函數[M].長春:吉林大學出版社,1991.

[4] 王長慶,姜俊彬.多值函數改變量及其在求解單值分支中的應用[J].遼寧師范大學學報,1997(4):347-350.

The Single-Valued Branches of Two Functions in Complex Number Field

FENG Zhi-xin
(College of Mathematics, Jilin Normal University, Siping, Jilin 136000, China)

In this paper, we make a systematic study of the single-valued branches of logarithmic function and radical function in complex number field by using “limiting argument” method and “continuous transforming” method.

multi-valued function; argument; function transforming; single-valued branches

O174.5

A

1673-2065(2012)01-0029-04

2011-09-26

吉林省教育廳“十二五”科學技術研究項目(2011- 160)

馮志新(1979-),女,吉林雙遼人,吉林師范大學數學學院講師,理學碩士.

(責任編校：李建明英文校對：吳秀蘭)