淺談降低數學概念學習難度的策略

嚴建文

【摘要】數學概念是學生必須掌握的重要基礎知識，是初中數學教學的重點內容.由于數學概念具有高度概括性、抽象性，初中學生對概念的學習因難理解和難記憶產生畏懼心理.本文從情景創設、過程體驗、概念理解和科學記憶四方面提出教學策略，激發學習興趣，透徹概念理解，實現知識遷移，降低概念學習難度，提高學生的數學素養.

【關鍵詞】數學概念學習；教學策略；降低難度

概念是思維的最基本單元，而數學概念是一類事物在數量關系和空間形式方面的本質屬性的抽象，是導出數學定理、法則的邏輯基礎.因此，數學概念的教學，是整個數學教學的一個重要環節.而數學概念本身具有高度概括性、抽象性和嚴謹性，概念的學習又帶有一定的系統性和延續性，若前面的概念沒掌握好，學習新的概念就更困難了.那么怎樣組織教學，才能降低學生學習概念的難度，更好地掌握數學概念呢？筆者結合多年的數學教學實踐，下面從四個方面談談降低數學概念學習難度的策略.

一、創設合理情景，激發學習興趣

建構主義教學理論認為：“知識并非被動地接受，而是有認知能力的個體在具體情境中與情境的相互作用而建構出來的，這樣獲得的知識才能真正為學生所擁有.”《數學課程標準》中倡導數學教學要啟發學生學習數學的興趣，要為學生提供豐富多彩的學習情境.數學概念有些是由生產、生活實際問題中抽象出來的，有些是由數學自身的發展而產生的.可見，數學概念教學中選擇恰當的數學素材，創設合適情境，化抽象為直觀，可以降低學生的理解難度，激發學習興趣，充分調動學生參與課堂教學活動的積極性.

１.利用學生熟知的感性材料

用來引入數學概念的材料是十分豐富的，可以是學生日常生活中所接觸的事物，也可以是教材中的實際問題及模型、圖形、圖表等.如直線與圓的位置關系可以海上日出為例，數軸以溫度計為例，等等.通過貼近學生的生活實例，來對相應的概念作出解釋，使學生從感性認識到理性認識，有利于學生加深對概念的理解.但要注意的是，教師提供的感性材料有時往往具有片面性，所以容易造成學生錯誤地擴大或縮小概念，因此要從多角度全方位加以補充說明.

２.利用多媒體教學的優勢

對于抽象的概念教學，教師可以充分利用多媒體的優勢，這樣不僅可以激發學生的學習興趣，還可以多方面調動學生的感官，由形象直觀的認識提高為抽象的概括，使抽象的數學知識以直觀的形式出現，從而突破難點.在初一階段進行“軸對稱”概念的教學中，我利用Ｆｌａｓｈ軟件制作了一只會飛的花蝴蝶，這只蝴蝶剛一“飛”上屏幕，立刻就吸引了全體同學的注意，一些平時不愛上數學課的學生這時也活躍起來.同學們根據蝴蝶的兩只翅膀在運動中不斷重合的現象很快就理解了“軸對稱”的定義.

３.指導學生動手操作

心理學家認為：思維是從動作開始的.同時新課程理念也倡導學生自主合作探究的學習方式.因此在概念教學時，就需要充分發揮學具操作的作用，可多讓學生親自動手試一試，在實驗中得出結論.如圓柱、圓錐的側面展開圖學習，可讓學生自做模型，然后用剪刀剪一剪，做一做.有關三視圖的教學讓學生從家里帶來軍棋子、冬瓜塊等東西，動手擺弄各種模型后進行觀察.這樣既體現了學生學習的主體地位，又活躍了課堂氣氛，學生通過動手、動腦經歷了發現數學概念的“演習”.

二、體驗概念形成，實現知識遷移

讓學生體驗概念的形成過程，即概念在什么條件下產生，在什么背景下初露端倪，如何經過分析、對比、歸納、抽象，最后形成理性的概念.這個過程，如果處理得當，對發展學生的數學思維很有利.

幾何概念是進行判斷、推理和建立定理的依據，也是思維的起點，應當向學生揭示概念間的相互聯系及其本質屬性.因此在幾何教學中，不僅應注意概念與圖形的結合，更要重視引導學生觀察、發現、探索、體驗概念的形成過程.例如在“四邊形”一章的四邊形定義教學中，若只停留在對四邊形定義的文字表述上是浮淺的，因為四邊形的概念的教學是聯系“三角形”一章與“四邊形”一章的紐帶，教學時要切實注意啟發學生觀察圖形，探索四邊形的組成，由學生概括：

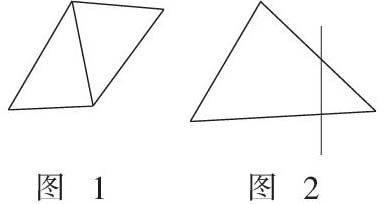
（１）四邊形可以看作是由兩個具有公共邊的任意三角形組成的.（圖1）

（２）四邊形也可以看作是一個大三角形任意截取一個小三角形后的剩余部分.（圖2）

通過上面的認識，學生很自然地從三角形的概念過渡到四邊形的學習上了.至于給四邊形下定義就輕而易舉地可以完成了，對認識四邊形的邊、對角線、頂點、內角都是順理成章的事.同時我們也不必再為后面幫助學生理解“把四邊形的有關問題轉化為三角形的問題來解決”的原因而多費口舌了.

三、重視概念理解，把握內在精髓

概念的理解是概念教學的中心環節，概念的獲得是學生經過分析、綜合、比較、抽象、概括的結果.只有在概念導入后，引導學生主動探索，激發學生的思維，才能做到真正理解概念.

１.理解概念要透徹

學習數學概念，不能囫圇吞棗，要求在講概念時講清、講透.對課本上的精練的概念應該字斟句酌，幫助學生徹底認清關鍵性的字眼，逐字逐句理解透徹，力求真正弄懂.例如：“含有兩個未知數，并且未知數項的次數是１的整式方程叫二元一次方程”.對這個定義，除了講清楚“元”與“次”的含義外，還要抓住“項”這個字眼做文章，使學生懂得這個定義如果丟了“項”字，則方程ｘｙ＝５也是二元一次方程.

２.加強概念的類比

有比較才有鑒別.許多數學概念相互之間聯系密切，講新概念時聯系已講的概念，比較它們之間的異同點.例如一元一次不等式與一元一次方程，在“一元”與“一次”上是相同的，不同的是前者含不等號，后者含等號.對于易混淆的概念的主要區別要特別強調.例如多項式與單項式的區別，主要是含不含加減運算；整式乘法與因式分解的區別，主要是積化和差或和差化積.

３.舉出錯例，讓學生辨析

舉出錯例即學生從正面接觸概念后，教師從概念的反面有針對性地創設一種錯誤的情景，引導學生深入到這種特定的情景中，運用已有的知識和經驗去分析錯因，去嘗試矯正.

如為了幫助學生認識“對頂角”的本質特征，教師可以出示一些圖形，讓學生判斷一下它們是否是對頂角.（如圖3）

通過教師引導學生先走進自己所設計的圈套，然后引導學生去找錯、糾錯，這樣更有利于學生對概念的理解，讓學生在反思中提高對數學概念的理解程度.

４.前后貫通，形成概念系統

數學是一門結構性很強的學科，任何一個數學概念都存在于一定的系統之中，并與其他有關概念有著區別與聯系.因此在進行概念教學時，要注意引導學生將所獲得的每一新概念及時地納入相應的概念系統，這樣新舊概念才能融會貫通，才能真正透徹地理解新概念，才能使相關聯的概念形成概念系統.這樣做也有利于學生所獲得的概念的保持與運用，有利于學生概念系統的形成，有利于學生認知系統結構的形成.如在學過菱形面積計算公式后，可以通過練習，聯系正方形是特殊的菱形，通過類比，可以發現正方形的面積計算公式可概括為“對角線的平方的一半”.這樣就溝通了知識間的內在聯系，鞏固了這一類概念的系統知識.

四、使用科學方法，形成永恒記憶

數學概念不僅僅要理解，還要對重要的概念、定理、定義、數學思想方法進行必要的識記.當然識記要在理解的基礎上進行，通過理解來幫助記憶，通過記憶來加深理解.

教學中要指導學生科學合理地記憶：①利用順口溜幫助記憶.如教學點的坐標寫法時，我編了口訣“橫在前，縱在后，中間有顆小豆豆，兩端勿忘添括號”，糾正了學生寫坐標時順序顛倒及忘添括號的錯誤，既生動又形象，學生印象非常深刻.②數形結合法幫助記憶.如講實數的絕對值時，既講其代數定義，又講其幾何定義，“數軸上表示一個數的點，它到原點的距離叫做這個數的絕對值”，讓學生看著數軸上的圖示記憶這一概念.特別是對于“三角函數”中的概念、公式，更要充分利用圖形幫助學生記憶.

不理解的記憶是機械記憶，是鸚鵡學舌，當然無用，只會加重學生的負擔，但是沒有科學記憶去談理解掌握概念，肯定是空話一句，也是不行的.課前預習與課后復習要安排時間讓學生熟悉、鞏固有關的基本概念、定理、定義，必要時要檢查，還要結合新課復習讓學生有一個循環的記憶過程.在例題講解中，盡可能聯系學生已往學過的概念.在學生稍有遺忘的時候，又刺激記憶，不斷加深印象，使學生真正記住，在需要時能立刻浮現腦際，脫口而出.

綜上所述，只要我們遵循認識規律，注重概念教學的研究與實踐，不斷優化數學概念教學策略，就一定能幫助學生降低數學概念學習的難度，使學生透徹理解數學概念，實現知識遷移，從而提高學生的數學素養.

【參考文獻】

［１］劉兼，孫曉天．數學課程標準解讀［Ｍ］.北京：北京師范大學出版社，２００４．

［２］周茂生．適時、適當利用反例［Ｊ］．中小學數學，２００７（９）．

［３］劉建華．讓學生“過目不忘”［Ｊ］.中小學數學，２００７（１０）．