立足境脈教學，促進素養落地

唐婷婷

摘? 要：境脈教學既包括問題情境、教學流程的脈絡，也包括學習者認知結構關系發展的脈絡.通過情境的脈絡發展關系把課堂的教學任務有機結合起來，學生主動使舊知與新知發生聯系，組織建構認知結構，并使之成為其自身知識網絡的一部分.

關鍵詞：境脈教學；核心素養；直線與平面垂直

《普通高中數學課程標準（2017年版2020年修訂）》指出高中數學課程要以學生發展為本，要優化結構、突出主線，要啟發思考、把握本質.在數學教學中，教師不僅要按照數學學科特點組織教學，更要尊重學生的已有經驗，幫助學生建立新的學習脈絡.教學活動從“教”走向“學”，從“累積知識”走向“涵育素養”，“境脈教學”由此誕生.

1? 境脈教學的內涵特征

境脈教學中的“境”即教學情境，“脈”即教學主線.境脈教學既包括問題情境、教學流程的脈絡，也包括學習者認知結構關系發展的脈絡.主題情境作為教學主線貫穿首尾、前后呼應，通過主題情境的脈絡發展關系把課堂的教學內容有機結合起來，學生主動地使舊知與新知建立關系、發生意義，組織建構認知結構，并使之成為其自身知識網絡框架的一部分.

2? 基于核心素養的教學設計

本文設計了突出學生主體地位并具有互動生成的教學情境，通過問題驅動衍生出學生自主探究的教學活動，落實了學生的知識與技能，提升了學生的核心素養.

2.1

教學目標設置

（1）通過觀察實例，說出直線與平面垂直的定義.

（2）借助直觀感知、探究類比、操作確認，得到直線與平面垂直的判定定理并會作出解釋.

（3）體會空間問題平面化、線線垂直與線面垂直的相互轉化.經歷合作探究，構建并完善知識結構.

2.2

教學重點難點

教學重點：直線與平面垂直的定義和判定定理的理解及應用.

教學難點：操作確認并概括出直線與平面垂直的判定定理.

2.3

教學過程設計

教學活動1? 溫習舊知，先驗新知接境

問題1? 請同學們回顧直線與平面的位置關系有哪些？我們已經學習了直線與平面平行的定義、判定、性質，大家想一想，接下來我們要學些什么呢？

【設計意圖】獲取研究對象，明確“為什么學”.

問題2? 通過類比“直線與平面平行”的學習過程，你認為要具體研究“直線與平面垂直”哪些方面的內容？需要采取什么研究方法？按怎樣的過程進行研究？

【設計意圖】研究“直線與平面垂直”這部分內容，其本質是研究兩類不同維數空間基本圖形的位置關系，引導學生找到與其具有類似結構的“直線與平面平行”進行類比，設計切實可行的研究思路，讓學生進一步明確“學什么”“怎么學”.在研究過程中，教師需引導學生挖掘內隱的思想方法：“降維”“平面化”.

教學活動2? 引入情境，創設任務啟境

問題3? 我們都知道，研究一類數學對象的起點是定義.那么，應該怎樣對“直線與平面垂直”下定義呢？

追問? 你能發現生活中直線與平面相交的例子嗎？

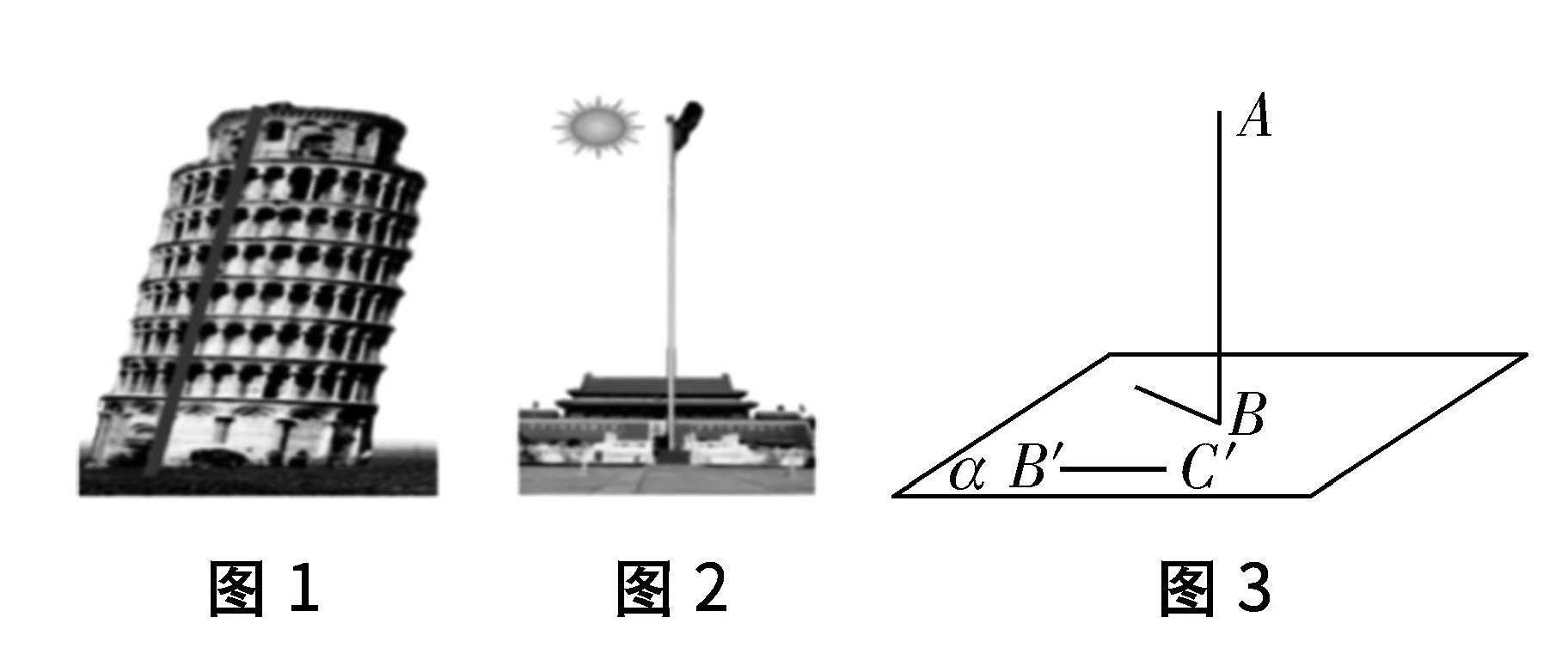
【設計意圖】克萊羅在《幾何基礎》中對直線與平面垂直的定義：“一條直線不向平面的任何一面傾斜，則直線與平面垂直.”圖1，圖2中比薩斜塔的“斜”，旗桿的“直”，說明生活中處處存在著直線與平面的斜交與垂直交，鼓勵學生體會生活中的數學，用數學的眼光觀察世界.

問題4? 觀察陽光下垂直于地面的旗桿，隨著時間的推移，旗桿影子所在的直線也在不斷地變化.如圖3，旗桿AB所在的直線與它的影子所在的直線垂直嗎？那么，旗桿AB與地面內不經過點B的直線也會垂直嗎？為什么？

追問? 你能嘗試給直線與平面垂直下定義嗎？

【設計意圖】學生能根據實際問題情境抽象概括出直線與平面垂直的定義，即“若一條直線垂直于平面上與該直線相交的所有直線，則該直線與平面垂直”.這與歐幾里得《幾何原本》中線面垂直的定義不謀而合.此時，教師引導學生進一步觀察，學生不難發現，對于平面內不過點B的任意一條直線B′C′，總能在平面上找到過點B的一條直線與之平行，根據異面直線垂直的定義可知AB⊥B′C′.因此，AB垂直于平面內的任意一條直線.進而，學生自主完善直線與平面垂直的定義，即“若一條直線垂直于平面內的任何一條直線，則直線垂直于平面”.

教學活動3? 回歸定義，學習脈動入境

問題5? 我們除了可以用定義來判斷直線與平面垂直，還有其他稍微簡便一點的方法嗎？

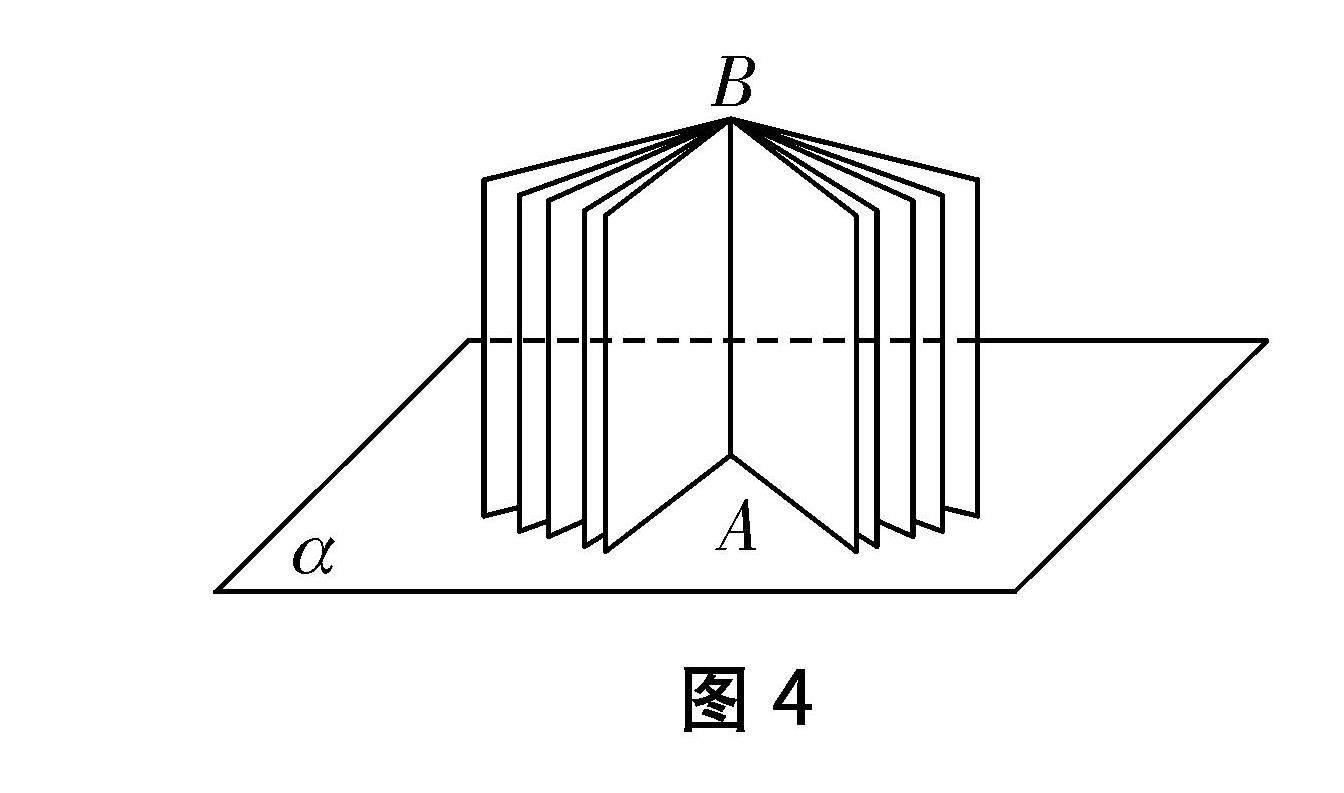
追問1? 通過觀察實物模型，如圖4，翻開一本書立于桌面，此時書脊AB與桌面是什么關系呢？通過直觀感知，思考只要滿足“什么條件”，就能使直線與平面垂直.

追問2? 可以通過怎樣的實驗來進行操作確認呢？請大家分小組完成相關操作.

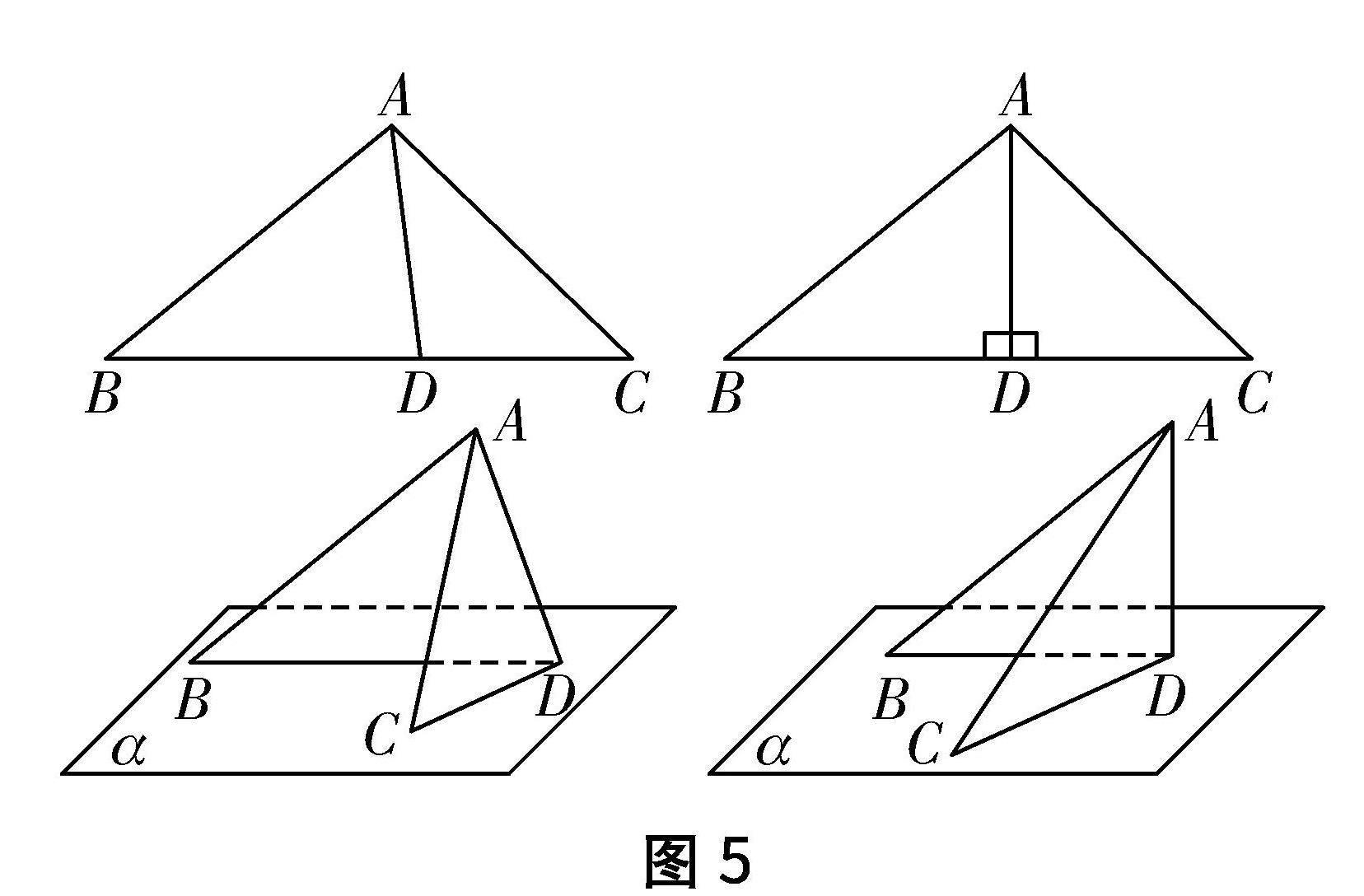
學生活動：圖5中，折紙操作，過△ABC的點A翻折紙片，得到折痕AD，將翻折后的紙片豎起置于桌面，驗證折痕AD與桌面是否垂直.

追問3? 類比直線與平面平行的判定定理的敘述方式，你能得出直線與平面垂直的判定定理嗎？

【設計意圖】類比直線與平面平行的判定定理，即將“直線與平面的平行”問題轉化成“直線與直線的平行”問題，體現了“降維”和“平面化”的思想方法.學生自主歸納直線與平面垂直的判定定理，即“如果一條直線與平面內的兩條相交直線垂直，那么直線與該平面垂直”.通過基本事實的推論2，學生想到：兩條相交直線可以確定一個平面，兩條平行線也可以確定一個平面.

教學活動4? 解決問題，形成聯動生境

問題6? 求證：如果兩條平行直線中的一條直線垂直于一個平面，那么另一條直線也垂直于這個平面.

【設計意圖】培養學生將文字語言轉化為圖形語言和符號語言的能力，用數學的思維思考，用數學的語言表達，引導學生養成從定義和判定定理尋找問題突破口的習慣.

變式? 在《九章算術》中，劉徽曾多次提到陽馬、鱉臑等幾何模型.文中將底面為長方形且有一條側棱垂直于底面的四棱錐稱為陽馬，將四個面都為直角三角形的四面體稱為鱉臑.在四棱錐P-ABCD中，側棱PD⊥底面ABCD，且PD=CD.試判斷四面體P-BCD是否為鱉臑，并證明.

【設計意圖】學以致用，學生通過體驗成功，不斷激發學習興趣.通過變式題，融入了數學文化，讓學生體會中國古代文化的博大精深.學生通過情境、學境、心境之間的境相交融，不斷優化知識框架結構.

教學活動5? 反思小結，建立脈絡出境

為什么學（研究的背景）？學什么（研究的內容）？怎樣學（研究的脈絡、思想方法）？你認為接下來學什么（嘗試新的探究）？

【設計意圖】教師鼓勵學生從基礎知識、基本方法、核心素養三個方面自主總結，并用流程圖輔助展示本節課外顯的探究歷程、內隱的思想方法.引導學生注重經驗關聯，學會遷移應用、舉一反三、適度拓展，進而建立新的學習脈絡.

3? 基于核心素養的境脈教學策略分析

境脈教學的原則是堅持設計為先、立足學生、實施為要、植根學習.情境性、探究性、脈絡性是其主要特征，落實核心素養是其根本目標.

3.1? 引入情境脈絡，讓新知生成有理有據

通過挖掘生活素材，構建情境境脈.教師選擇貼近學生實際的旗桿和影子的情境設計教學活動，驅使學生自主探究，主動優化直線與平面垂直的定義，促使新知后形成有理有據.

3.2

圍繞活動脈絡，讓課堂教學更具厚度

本節課通過類比直線與平面平行的判定定理的形成過程，學生通過直觀感知、探究發現、操作確認，得到“一條直線垂直于一個平面內的兩條相交直線即為直線與平面垂直的判定定理”，符合學生的最近發展區.在判定定理的形成過程中，教師不斷引導學生感受探究過程中“降維”“平面化”的思想方法，做到課堂教學簡約而不簡單，還數學以思維的本質，使數學課堂更加豐滿、厚重，讓學生享受其中.

3.3

形成知識脈絡，讓素養脈絡根植課堂

形成知識脈絡，即要求教師將知識的演繹結構轉化為學生的認知結構，納入學生已有的知識體系，為形成新知奠定基礎.學生利用已有的知識經驗，從知識境脈、經驗境脈中提取自己所需要的學習內容，自主建構數學新知.通過本節課的學習，學生在情境中嘗試解決問題，在經歷中學會了直線與平面垂直的判定方法，在經驗中進行了遷移運用，通過不斷完善自身知識結構，為接下來學習直線與平面垂直的性質定理做好鋪墊，從而多維度提升經驗建構的深度體驗.

境脈教學有利于學生深度理解和剖析數學學習的內容和本質，真正意義上從“教師的教”轉向“學生的學”，從“知識的學習”轉向“本質的體悟”，從“數學知識累積”轉向“學科涵養化育”.境脈教學給師生帶來了更多經驗建構、解決問題、學習成長的契機和路徑，在潛移默化中促進學生的數學核心素養落地.