不等式導數問題常見題型及其解題策略

廖妍婷 楊楚鋒 巫輝瑩 巫陽洋 梁填 張文超

摘? 要：導數與不等式、函數交匯綜合是高考命題的熱點.這類題型主要以選擇題、解答題的形式為主，往往涉及了函數性質、導數的應用、不等式的求解等多個方面，需要學生具備較強的數學綜合能力和思維能力.本文通過歸納常見的不等式導數問題并給予相應解題策略，以此來幫助學生更好地分析并掌握解決該類題型的方法和技巧.

關鍵詞：不等式導數；函數；高考；解題策略

不等式導數問題在高考命題中占據重要地位，在高考試卷中經常以選擇題和解答題的形式命題，有基礎題，也有中檔題，更多時候是作為“把關題”出現，承擔著區分與選拔優秀學生的功能.隨著教育改革的深入，高考題目靈活多變，新課標指出“基于數學核心素養的教學評價，不僅要關注學生對知識技能的掌握程度，還要更多地關注學生的思維過程”.不等式導數問題涉及化歸、方程、分類討論等數學思想，同時考查導數和不等式的基礎知識，難度逐級遞增、環環相扣，這對于培養學生的數學思維、邏輯推理能力具有重要意義.

1? 歷年高考不等式導數問題的出題特點

1.1? 考查題量、題型分析

高考改革一直是近年來的熱點，在“新課標，新教材，新高考”這一背景下，不等式導數問題又有哪些變化呢？下文主要從近年來高考試卷考查題量、題型方面來分析.

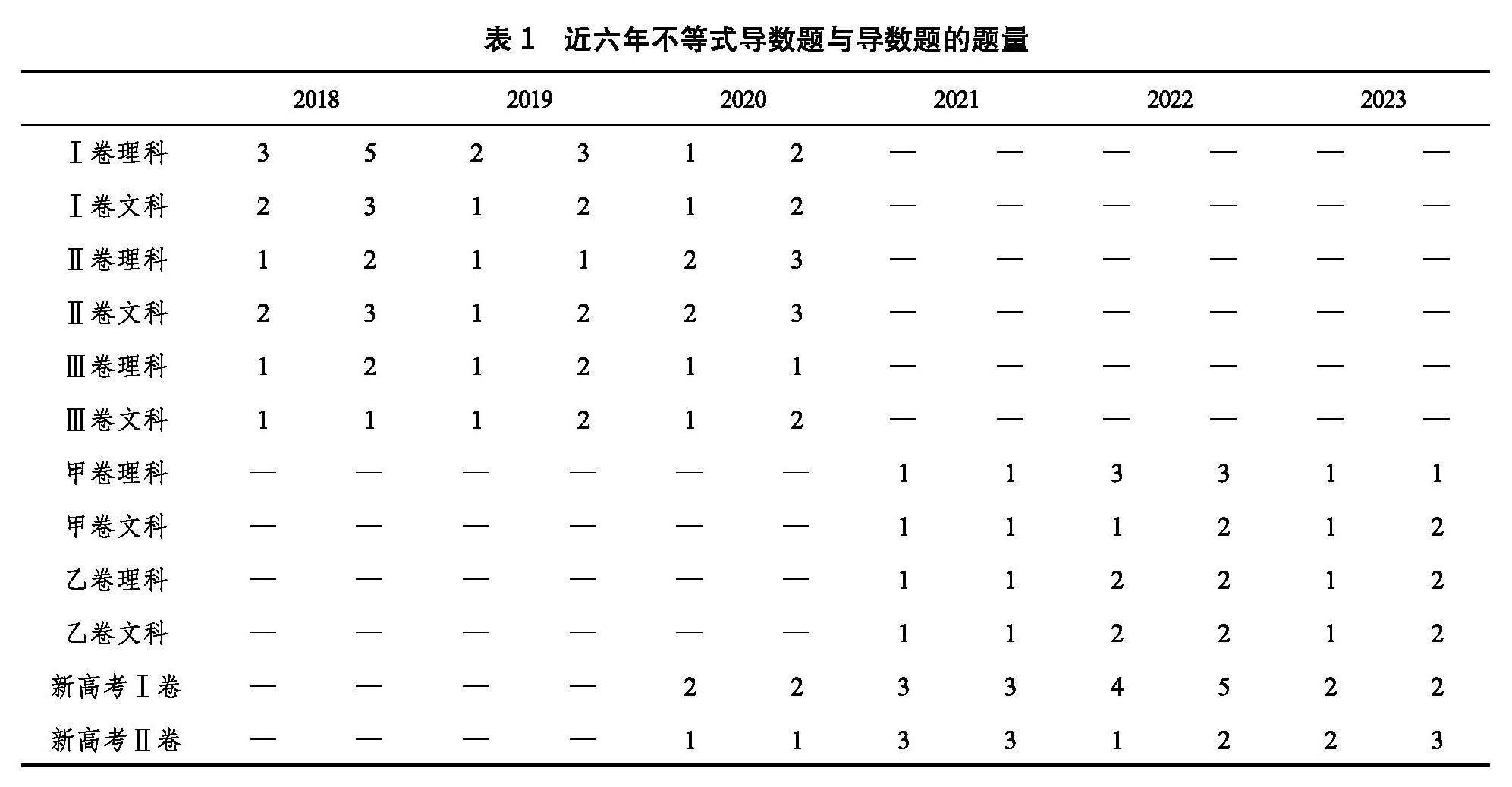
首先從考查題量方面分析.近六年全國Ⅰ卷、Ⅱ卷、Ⅲ卷，以及新高考全國甲卷、乙卷、Ⅰ卷、Ⅱ卷共38套，考查導數題共82道，其中不等式導數題共考查了59道，占比72.0%.在實施新高考前，不等式導數在導數題中考查占比為60.7%.實施新高考后，不等式導數題的比重相比舊高考有所提升.如2022年不等式導數在導數占比為81.3%，2023年不等式導數在導數占比為66.7%.具體考查題數見表1，表中每個年份的左側為不等式導數的考查題量，右側為導數的考查題量.

從題型方面分析.分析近幾年高考試卷，不難發現導數中不等式常考問題可以總結為以下八大題型，分別是函數導數的單調性與不等式、函數零點問題、函數極值問題、證明含參不等式恒成立、不等式恒成立求參數的取值范圍、存在性變量問題、數列不等式、極值點偏移.如在2022年新高考全國Ⅱ卷22（2）、22（3）分別考查了不等式恒成立求參數的取值范圍和導數中的數列不等式.在2023年新高考Ⅰ卷19（2）考查了證明含參不等式恒成立，22（2）考查了函數導數的單調性與不等式以及極值問題等.

1.2? 考查題型、解題策略分析

針對這八大題型，下文通過從解題方法方面剖析2022，2023年新高考Ⅰ卷、Ⅱ卷不等式導數試題并總結常用的三種解題策略.表2呈現了近幾年部分不等式導數試題以及其解題方法.

從表2，我們可以清楚地看到構造函數法、切線放縮法常用于解決不等式導數問題.此外，在對其他地區的高考試卷分析中，發現在2023年全國甲卷文科20（2）可以用極值點偏移法解答，2022年全國甲卷理科21（2）的解答同樣用到了極值點偏移的方法.總結歸納近幾年不等式導數試題，可以發現構造函數法、切線放縮法、極值點偏移法最常用于解決不等式導數問題.

2? 不等式導數問題的三種解題策略

2.1

構造函數法

例1? ^^［2023年新高考全國Ⅱ卷數學22（1）］&&證明：當0

解析：構造函數g（x）=x-x2-sinx，x∈（0，1），求導，得g′（x）=1-2x-cosx.

令p（x）=g′（x），則p′（x）=-2+sinx<0.

所以有g′（x）在（0，1）上單調遞減.

故g′（x）

所以g（x）在（0，1）上單調遞減.

可得g（x）

構造函數h（x）=x-sinx，x∈（0，1），求導，得h′（x）=1-cosx.

易知h′（x）>0，所以h（x）在（0，1）上單調遞增.

所以h（x）>0-sin0=0，即sinx

評注：這道題目屬于中檔題，主要是將函數單調性和不等式證明結合起來，要求學生能夠根據函數的單調性判斷函數的值域，并利用函數的性質進行不等式的證明.此外還要求學生能夠將所學知識綜合運用，解決一些較為復雜的不等式問題.主要考查了學生的綜合應用能力和邏輯思維能力.

技巧：在運用構造函數法解決不等式導數問題時，可以通過以下步驟進行解答：

（1）觀察不等式的形式和已知條件，確定構造函數的形式，如已知函數f（x）在某區間內的最小值為n，則可以構造函數F（x）=f（x）-nx（其中n為某常數）；

（2）根據導數與函數單調性的關系，判斷構造函數的單調性；

（3）利用單調性求解不等式.

2.2? 切線放縮法

例2? ^^（2023年新高考全國Ⅰ卷數學19）&&已知函數f（x）=a（ex+a）-x.

（1）討論f（x）的單調性.

（2）證明：當a>0時，f（x）>2lna+32.

解析：（1）先求導，再對a分類討論，從而判斷a的不同取值范圍下f（x）的單調性.

（2）解法一：（切線放縮）

利用ex≥x+1.

則f（x）=a（ex+a）-x=ex+lna+a2-x≥x+lna+1+a2-x=a2+lna+1.

令g（a）=1+a2+lna-2lna+32=a2-lna-12，則g′（a）=2a-1a=2a2-1a.

令g′（a）>0，得a>22；令g′（a）<0，得0

故g（a）在0，22上單調遞減，在22，+∞上單調遞增.

故g（a）≥g22=12-ln22-12>0，所以f（x）>2lna+32，證畢.

解法二：（同構+切線放縮）

當a>0時，要證f（x）>2lna+32.

即證ex+lna-（x+lna+1）+12（a2-lna2-1）+12a2>0.

又ex≥x+1，故ex+lna-（x+lna+1）≥0.

又lnx≤x-1，故12（a2-lna2-1）≥0.

又12a2>0，故ex+lna-（x+lna+1）+12（a2-lna2-1）+12a2>0顯然成立.證畢.

評注：這道題目主要考查了函數的單調性和極值定理的應用，以及極限的性質.在解決題目時使用切線放縮公式能達到事半功倍的效果.要求學生有較強的綜合應用能力和邏輯思維能力，有助于提高學生的思維品質和解決問題的能力.

技巧：確定目標函數、構造切線函數、分析切線函數的性質（導數、單調性、極值等）、利用切線函數的性質證明不等式.以下為常見的放縮不等式.

（1）切線放縮：對于函數f（x），其導數為f′（x），則有f（x）≥f（x0）+f′（x0）（x-x0）.

（2）指數函數放縮：對于x>0，有ex≥x+1.

（3）對數函數放縮：對于x>0，有ln（1+x）≤x和ln（1+x）≥2x2+x.

（4）三角函數放縮：對于x≥0，有sinx≥x-x33！和cosx≥1-x22！.

（5）代數式放縮：對于正整數n，有1+1nn

2.3

極值點偏移法

例3? ^^（2022年高考全國甲卷理科21）&&已知函數f（x）=exx-lnx+x-a.

（1）若f（x）≥0，求a的取值范圍.

（2）證明：若f（x）有兩個零點x1，x2，則x1x2<1.

解析：（1）由導數確定函數單調性及最值，即可得解.

（2）解法一：（構造函數與極值點偏移）

不妨設0

又x2，1x1∈（1，+∞），f（x）在（1，+∞）上單調遞增，f（x1）=f（x2），即證f（x1）-f1x1<0.

故當x∈（0，1）時，要證x1x2<1，即證明exx-lnx+x-xe1x-lnx-1x<0.

令g（x）=exx-lnx+x-xe1x-lnx-1x，則g′（x）=（x-1）（ex-xe1x+x-1）x2.

令h（x）=ex-xe1x+x-1，易得h′（x）>0.

即h（x）在（0，1）上單調遞增，h（x）

則g′（x）>0，g（x）在（0，1）上單調遞增，即g（x）

解法二：（對數均值不等式與極值點偏移）

令t=exx>1，則f（t）=t+lnt-a，f′（t）=1+1t>0.

所以f（t）=t+lnt-a在（1，+∞）上單調遞增，故f（t）=0只有1個解.

又f（x）=exx+lnexx-a有兩個零點x1，x2，故t=ex1x1=ex2x2.

兩邊取對數，得x1-lnx1=x2-lnx2，即x1-x2lnx1-lnx2=1.

要證x1x2x2>0.

則有lnx1-lnx2

即證lnx1x2

設t=x1x2>1，則2lnt

構造h（t）=2lnt-t+1t，t>1，則h′（t）=2t-1-1t2=-1-1t2<0.

故h（t）=2lnt-t+1t在（1，+∞）上單調遞減，h（t）

故x1x2<1，即x1x2<1.

評注：本題屬于難題，通過設置綜合性的導數不等式問題和較為復雜的情境，重視基于數學素養的關鍵能力的考查，具有較好的選拔功能，考查了學生靈活應用函數、不等式思想解決復雜問題的能力，對直觀想象能力和邏輯推理能力也有較高的要求.

3? 總結與展望

不等式導數問題在高考命題、數學研究中占據核心地位，對數學的發展和應用具有重要意義.解決這類題型對于提高學生的數學素養和解決問題的能力都具有重要的價值.

本文通過對標歷年高考試卷，歸納出八大題型，即函數導數的單調性與不等式、函數零點問題、函數極值問題、證明含參不等式恒成立、不等式恒成立求參數的取值范圍、存在性變量問題、數列不等式、極值點偏移，并總結出三大解題策略——構造函數法、切線放縮法、極值點偏移法，此外對這三類方法分別進行研究并總結做題技巧.

希望學生能熟練掌握解決不等式導數問題的技巧，學習其數學思想，領略數學魅力，也希望各位數學教育工作者能提出更多更精妙的解決不等式導數問題的策略，教學相長，共同進步！

參考文獻

［1］ 李笑竹.高中數學學科核心素養的培養途徑探究［J］.科學咨詢（教育科研），2021（1）：171.

［2］ 中華人民共和國教育部.普通高中數學課程標準（2017年版）［M］.北京：人民教育出版社，2018.

［3］ 劉灝.利用構造法解決極值點偏移問題——以2022年高考全國甲卷理科數學第21題為例［J］.數理化解題研究，2023（25）：40-42.

［4］ 趙林.合理運用放縮法 有效破解證明不等式難題［J］.數理化解題研究，2021（19）：36-37.

［5］ 周小鋒.利用導數證明不等式的技巧策略［J］.中學生數理化（高考數學），2023（5）：21-23.

［6］ 鄭堅幟.數學建模視角下與導數有關的不等式問題妙解路徑［J］.中學數學研究，2023（10）：47-50.

［7］ 敖羚峰.高中數學導數試題分析、解題錯誤與教學對策研究［D］.上海：華東師范大學，2021.