增強(qiáng)代數(shù)推理 提升幾何直觀

徐境鴻

摘要：2023年廣西中考數(shù)學(xué)第24題源于課本和課程標(biāo)準(zhǔn)，創(chuàng)新命題形式，將代數(shù)與幾何完美結(jié)合，有效考查了學(xué)生的幾何直觀和推理能力.文章以該題為研究對象，對題目進(jìn)行詳細(xì)分析，尋本溯源，并對歷年中考此類型試題的考查特點進(jìn)行探究，然后對試題的命制進(jìn)行反思總結(jié)，旨在通過對中考試題的研究，使教與學(xué)更具有針對性，為中考復(fù)習(xí)備考提供參考.

關(guān)鍵詞：中考數(shù)學(xué)；代數(shù)推理；幾何直觀；命題

中圖分類號：G632文獻(xiàn)標(biāo)識碼：A文章編號：1008-0333（2024）11-0008-03

2023年的中考已經(jīng)落下帷幕，在“雙減”政策背景下，廣西首次省級統(tǒng)一命題，這一轟轟烈烈的改革在今年中考釋放了大量信號，中考的指揮棒為中考備考指明了方向.本次中考試題圍繞核心素養(yǎng)，依標(biāo)務(wù)本，最大的亮點是降低了難度，減少模式化試題，增加了綜合實踐性、情境探究性、跨學(xué)科類題目的考查.不難發(fā)現(xiàn)，第24題是一道既經(jīng)典又創(chuàng)新的試題，現(xiàn)就該題進(jìn)行詳細(xì)的探究.

1 試題呈現(xiàn)

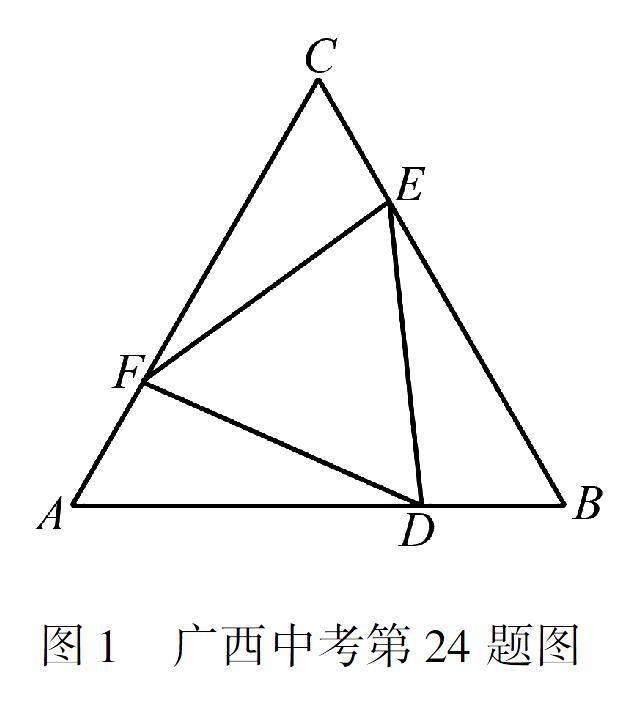
如圖1，ΔABC是邊長為4的等邊三角形，點D，E，F(xiàn)分別在邊AB，BC，CA上運(yùn)動，滿足AD=BE=CF．

（1）求證：△ADF≌△BED；

（2）設(shè)AD的長為x，△DEF的面積為y，求y關(guān)于x的函數(shù)解析式；

（3）結(jié)合（2）所得的函數(shù)，描述△DEF的面積隨AD的增大如何變化．

2 試題分析

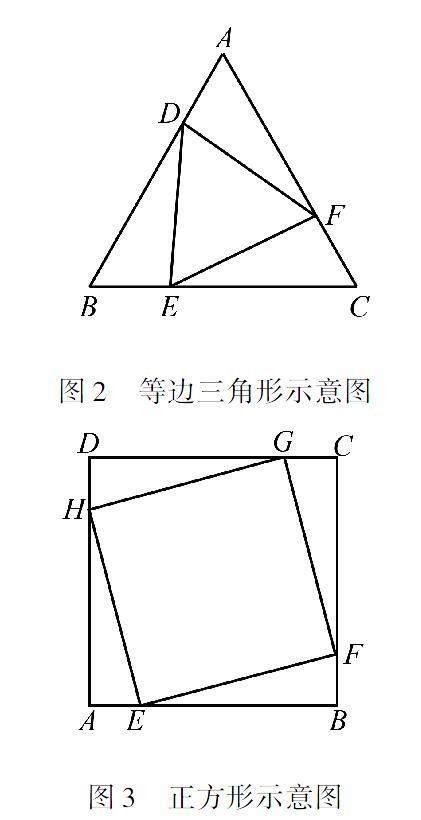
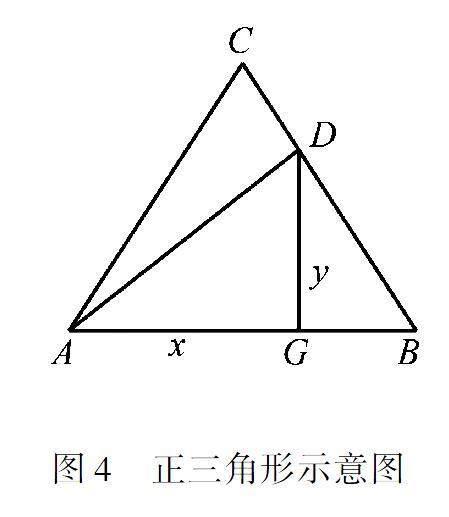
本題源于課本和課程標(biāo)準(zhǔn)，將代數(shù)與幾何完美結(jié)合，有效考查了學(xué)生的推理能力和幾何直觀.本題改變了往年中考放置壓軸題的位置，今年放在了24題，大大降低了難度.本題主要考查三角形全等、等邊三角形的性質(zhì)、動點、銳角三角函數(shù)、二次函數(shù)的綜合及函數(shù)的概念.掌握三角形的性質(zhì)、銳角三角函數(shù)，理解并掌握函數(shù)概念的本質(zhì)、二次函數(shù)的性質(zhì)是解決本題的關(guān)鍵.這是一道既常規(guī)又新穎的試題，該題由淺入深，逐步遞增難度，合理設(shè)置問題層次，每個問題之間均有邏輯關(guān)聯(lián)，符合學(xué)生的心理特征，注重考查學(xué)生的思維過程，體現(xiàn)學(xué)科思想的連貫性、邏輯性、嚴(yán)謹(jǐn)性等.

問題（1）主要考查全等三角形的證明，全等的條件比較明顯，屬于基礎(chǔ)內(nèi)容，學(xué)生易得分.問題（2）是一道典型的用代數(shù)式表達(dá)幾何結(jié)論的問題，考查數(shù)形結(jié)合思想，此問題有一定的難度，如果能突破此問題，則問題（3）就容易解決.近幾年，學(xué)生受應(yīng)試思潮的影響，對二次函數(shù)出現(xiàn)了一些比較固化的試題模型，如用待定系數(shù)法求函數(shù)解析式，某些點的確定性和存在性問題.學(xué)生對函數(shù)的理解不到位，教師缺少關(guān)注學(xué)科本質(zhì).該題的實質(zhì)就是考查學(xué)生對函數(shù)概念本質(zhì)的理解，讓學(xué)生體會函數(shù)是描述一個變化過程的工具.由于很多學(xué)生理解不透徹，所以這一問題對學(xué)生來說有一定難度.問題（3）是對函數(shù)概念性質(zhì)的進(jìn)一步理解和鞏固，評分細(xì)則從學(xué)生對知識理解的深度進(jìn)行分層賦分，隱含了命題關(guān)于過程評價的重要思路.學(xué)生在答題時，如果只答出“先減后增”可得1分，如果能答出“當(dāng)2

總之，該題不僅從幾何的角度考查了學(xué)生的幾何直觀，還從代數(shù)角度增強(qiáng)了學(xué)生的推理能力，是一道典型的幾何與代數(shù)結(jié)合且難度中等的題目.

3 尋本溯源

3.1 源于課本

如圖2，在等邊△ABC的三邊上，分別取點D，E，F(xiàn)，使AD=BE=CF，求證：△DEF是等邊三角形. （人教版八年級數(shù)學(xué)上冊第十三章《軸對稱》第93頁第11題）

如圖3，點E，F(xiàn)，G，H分別位于正方形ABCD的四條邊上．四邊形EFGH也是正方形．當(dāng)點E位于何處時，正方形EFGH的面積最小？（人教版九年級數(shù)學(xué)上冊第二十二章《二次函數(shù)》第52頁第7題）

3.2 源于課程標(biāo)準(zhǔn)

如圖4，正三角形ABC的邊長為1，D是BC邊上的一點，過D作AB的垂線，交AB于G，用x表示線段AG的長度.顯然，Rt△GBD的面積y是線段長度x的函數(shù)，試給出這個函數(shù)的表達(dá)式[2].（《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》第146頁例69）

4 試題研究

初中階段，不僅在數(shù)與代數(shù)領(lǐng)域有推理或證明的內(nèi)容，在幾何與圖形領(lǐng)域也有推理或證明的內(nèi)容.《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》新增了“了解代數(shù)推理”的內(nèi)容要求，可見幾何直觀與代數(shù)推理綜合的重要性.為此，筆者對比了近六年的北部灣經(jīng)濟(jì)區(qū)中考題，發(fā)現(xiàn)函數(shù)與幾何綜合題每年都考，將其匯總并分類，如表1所示.

從題目位置上看，前面幾年的此類題型基本在壓軸題位置，難度較大，對學(xué)生的要求很高，但是今年放到了24題的位置，要求和難度降低了，變化較大.從考查內(nèi)容上看，以前多是以二次函數(shù)的圖象為背景進(jìn)行考查，今年則是以等邊三角形這一簡單幾何圖形為背景.從考查形式上看，以前都是直接求定值，今年則是半開放式的“描述變化過程”，可見題目由固定式逐漸轉(zhuǎn)向理解式，模式化和機(jī)械性的題目在減少，過程性考查增加.

5 命題反思

5.1 重視教材，緊扣課程標(biāo)準(zhǔn)

通過對多年中考題的研究，我們發(fā)現(xiàn)幾乎每道題目都能在課本或課程標(biāo)準(zhǔn)找到母題，或是將母題的條件結(jié)論、背景框架、解題方法等進(jìn)行改編，或是在思想方法上重新立意進(jìn)行“包裝”.不管如何改編，試題在命制時均未超出課程標(biāo)準(zhǔn)的學(xué)業(yè)要求和能力要求.因此，在今后的命題中要嚴(yán)格依據(jù)課程標(biāo)準(zhǔn)，注重教材為本，關(guān)注學(xué)生的基礎(chǔ)知識，以學(xué)生理解為目標(biāo)改編，減少機(jī)械性題目.

筆者整理了課本中部分幾何與代數(shù)相結(jié)合的典型題目，僅供讀者參考.①九年級上冊第2頁無蓋紙盒問題；②九年級上冊第20頁邊框問題；③九年級上冊第52頁三角形、四邊形問題；④九年級上冊第57頁籬笆問題；⑤九年級上冊第125頁幾何圖形與反比例函數(shù)問題；⑥九年級下冊第44頁三角形與一次函數(shù)問題；⑦九年級下冊第58頁三角形、矩形與二次函數(shù)問題.

5.2 落實核心素養(yǎng)

數(shù)學(xué)新課程標(biāo)準(zhǔn)的亮點之一就是核心素養(yǎng)的提出與細(xì)化：會用數(shù)學(xué)的眼光觀察現(xiàn)實世界，會用數(shù)學(xué)的思維思考現(xiàn)實世界，會用數(shù)學(xué)的語言表達(dá)現(xiàn)實世界.初中階段具體表現(xiàn)有九個方面，命題應(yīng)覆蓋數(shù)學(xué)核心素養(yǎng)的各個方面.考查數(shù)學(xué)思維和解決問題的能力，命題可以設(shè)計一些開放性的問題，要求學(xué)生進(jìn)行分析、推理和判斷.考查數(shù)學(xué)方法的靈活運(yùn)用，命題可以涉及不同的數(shù)學(xué)方法和技巧.考查數(shù)學(xué)實踐和應(yīng)用能力，命題可以多創(chuàng)設(shè)情境，引導(dǎo)學(xué)生通過數(shù)學(xué)建模解決問題.通過各種措施的落實，可以確保命題符合數(shù)學(xué)核心素養(yǎng)的要求，能夠全面考查學(xué)生的數(shù)學(xué)能力和素養(yǎng)水平.同時，也能夠激發(fā)學(xué)生對數(shù)學(xué)的興趣和熱愛，促進(jìn)他們的數(shù)學(xué)學(xué)習(xí)和發(fā)展.

5.3 重視新題型

今年中考題有以下特點：創(chuàng)設(shè)真實問題情境，注重情景化試題；加大開放探究力度，激發(fā)創(chuàng)新與探究意識；重視動手操作能力，加強(qiáng)尺規(guī)作圖考查；增加試題閱讀量，提升信息處理能力；增設(shè)跨學(xué)科試題，培養(yǎng)綜合學(xué)科素養(yǎng)；重視數(shù)學(xué)傳統(tǒng)文化，關(guān)注學(xué)生文化素養(yǎng).因此，在復(fù)習(xí)備考中，教師要以此為導(dǎo)向，在日常教學(xué)中不斷滲透數(shù)學(xué)方法，適時總結(jié)，在命題中要重視以上題目的練習(xí)，讓學(xué)生從適應(yīng)到熟練再到舉一反三，最終從容面對中考.

參考文獻(xiàn)：

［1］ 劉昆.學(xué)業(yè)質(zhì)量為依據(jù) 關(guān)注學(xué)科本質(zhì) 聚焦核心素養(yǎng) 引領(lǐng)課題教學(xué)[J].中小學(xué)課堂研究，2023（S01）：14-17.

[2] 中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）[M].北京：北京師范大學(xué)出版社，2022.

［責(zé)任編輯：李璟］